Прямая и плоскость в пространстве

Пример 1. 1. Установить взаимное расположение прямой и плоскости, в случае их пересечения – найти координаты пересечения:

Решение. 1) 1) и

Определим координаты направляющего вектора прямой по ее каноническим уравнениям. Это вектор Нормальный вектор плоскости имеет координаты Найдем скалярное произведение векторов и :

Значит, и прямая L и плоскость P параллельны. Проверим, не лежит ли прямая L в плоскости P. Для этого определим принадлежность точки плоскости P, подставив координаты в уравнение плоскости:

Следовательно, а значит,

2

2) и

Прямая имеет направляющий вектор и точку Выясним, будет ли перпендикулярен нормальному вектору заданной плоскости

Осталось проверить принадлежность точки плоскости:

Значит, прямая L лежит в плоскости P.

3. 3) и

Направляющий вектор заданной прямой и направляющий вектор плоскости не коллинеарны и не перпендикулярны, т. к. и Значит, . Найдем координаты точки пересечения прямой и плоскости. Для этого перейдем сначала к параметрическим уравнениям прямой:

Затем в уравнение плоскости P подставим вместо их выражение через параметр t:

Откуда имеем

Подставим найденное значение параметра t в параметрические уравнения прямой:

Итак, .

Пример 2. Найти координаты точки N, симметричной точке относительно прямой, проходящей через точки и .

Решение. Для решения задачи воспользуемся следующими рассуждениями: симметричная точке M точка N находится в той же плоскости, что прямая AB и точка M, лежит на перпендикуляре MN к прямой AB и находится от прямой AB на том же расстоянии, что и точка M.

Пусть Тогда

1) – компланарны;

2) ;

3) ;

4) середина отрезка MN лежит на прямой AB.

Составим систему уравнений, используя координатную форму записи условий 1–3.

– компланарны при условии т. е. откуда получаем

откуда

Условие равносильно условию или что приводит к уравнению

затем

откуда

.

следовательно,

После подстановки , получим или

Таким образом, точки и удовлетворяют первым трем условиям. Осталось проверить четвертое. Найдем середины и отрезков и соответственно и проверим, какая из точек ( или ) лежит на прямой

ли

или

т. к. но

т. к.

Итак,

Пример 3. Прямая L задана общими уравнениями

Написать уравнение ее проекции на координатную плоскость Oxz.

Решение. Построим канонические уравнения прямой L. В качестве направляющего вектор можно взять вектор где Тогда

т. е.

Присвоив переменной x значение 0, получим систему уравнений из которой найдем а значит точка лежит на прямой L.

Таким образом, канонические уравнения прямой L таковы:

что эквивалентно системе трех уравнений, описывающих три плоскости, проектирующие прямую на координатные плоскости Oxy, Oxz и Oyz соответственно.

Итак, искомое уравнение

. Поверхности второго порядка

Пример 1. Использовать форму и построить поверхность заданную уравнением

Решение. Используем при исследовании геометрических свойств и форм поверхности метод сечений.

Определим сечение поверхности плоскостями где параллельными координатной плоскости Oxy:

Очевидно, что это кривые, проекции которых на ось Oxy задаются уравнение

(1)

Уравнение (1) при не имеет решений относительно Это означает, что соответствующее сечение есть пустое множество точек, а значит, рассматриваемая поверхность целиком расположена ниже плоскости При уравнение (1) определяет эллипс

с полуосями и вырождающийся в точку (0, 0, 1) при Заметим, что все эллипсы, получающиеся в сечениях поверхности плоскостями подобны между собой, причем с уменьшением их полуоси неограниченно монотонно возрастают.

Дальнейшее уточнение форм можно получить, рассматривая сечения координатными плоскостями Oxz и Oyz:

и

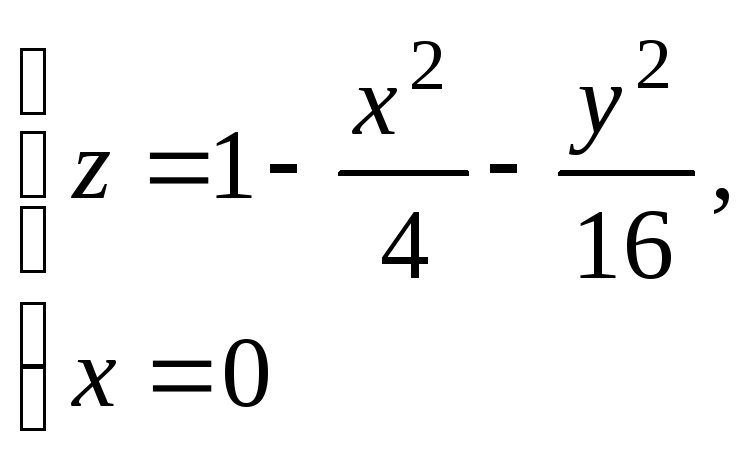
Имеем в первом случае кривую т. е. параболу с параметром вершиной в точке и ветвями, направленными в отрицательную сторону оси Oz. Во втором – параболу с параметром вершиной в точке и аналогичным направлением ветвей.

Выполненное исследование позволяет построить заданную поверхность (рис. 1). Это эллиптический параболоид с вершиной в точке (0, 0, 1), направленный в сторону убывания значений z с осью симметрии Oz.

Рис. 1.

Пример 2. привести уравнение к каноническому виду и определить тип поверхности, которую оно задает:

1)

2)

3)

4)

Решение. Воспользуемся методом выделения полных квадратов.

1) Преобразуем левую часть уравнения:

Значит, уравнение равносильно

или

Имеем уравнение однополосного гиперболоида, центр которого находится в точке (–1, 1, 2) и ось, прямая, параллельная оси Oz и проходящая через точку (–1, 1, 2).

2) Так как

то заданное уравнение равносильно уравнению

или что приводит окончательно к уравнению гиперболического параболоида следовательно в точку (-1, 0, 1).

3)

Поэтому имеем

или

Это уравнение эллипсоида с центром в точке (3, – 1, 2).

4) приводится к уравнению

Это уравнение эллиптического цилиндра смещенного в точку (– 2, 5, 0).

Примеры 3. Построить тело, ограниченное указанными поверхностями:

Решение. 1. – уравнение плоскости. Перейдя к уравнению плоскости «в отрезках», получим

что означает пересечение плоскости координатных осей в точках (3, 0, 0), (0, 3, 0) и (0, 0, 3) соответственно.

2. Уравнение задает круговой цилиндр, осью которого служит Oz, – координатная плоскость Oxy.

3. Сделаем эскиз тела (рис. 2 а, б)

Рис. 2, а.

Рис. 2, б.