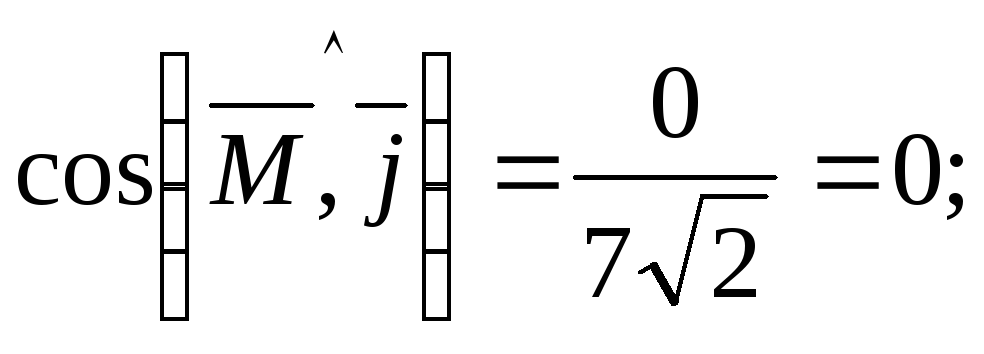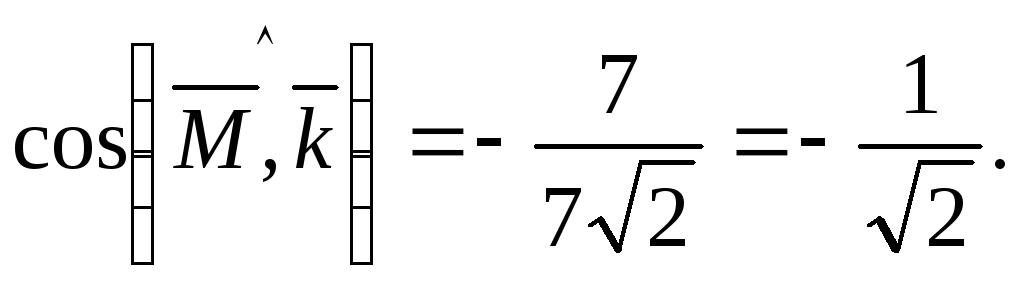В.4 Матрицы и операции над ними
Пример 1. Найти 2A – 3B, если
.
Решение. Прежде всего, следует заметить, что матрицы A и B имеют одинаковый размер 2×3. Поэтому, по определению линейных операций над матрицами, имеем
Пример 2. Вычислить соответствующие произведения (если возможно) и проверить справедливость равенства AB=BA для следующих пар матриц:
1)
5)
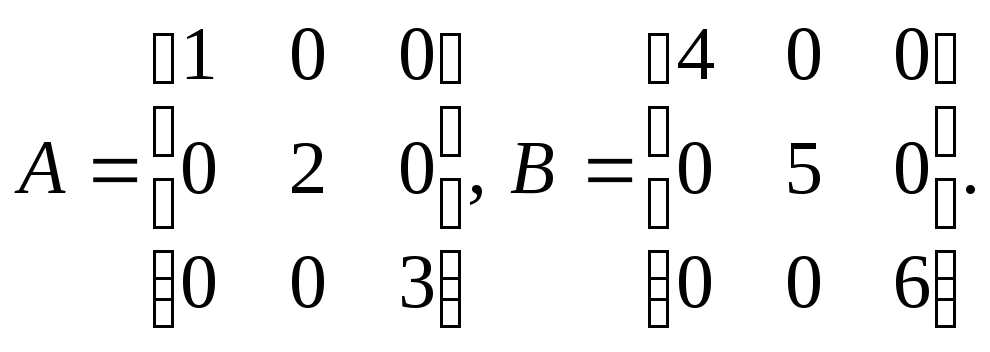
Решение. 1) Матрицы A и B согласованные, так как A имеет размер 2×2, а матрица B – размер 2×3:
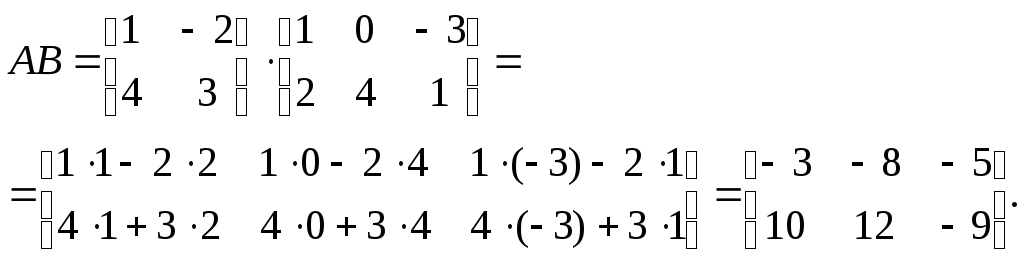
Умножение B на A невозможно, так как матрицы
В.5 ,6 Определители, их свойства и вычисление
Пример 1.
Вычислить
определитель
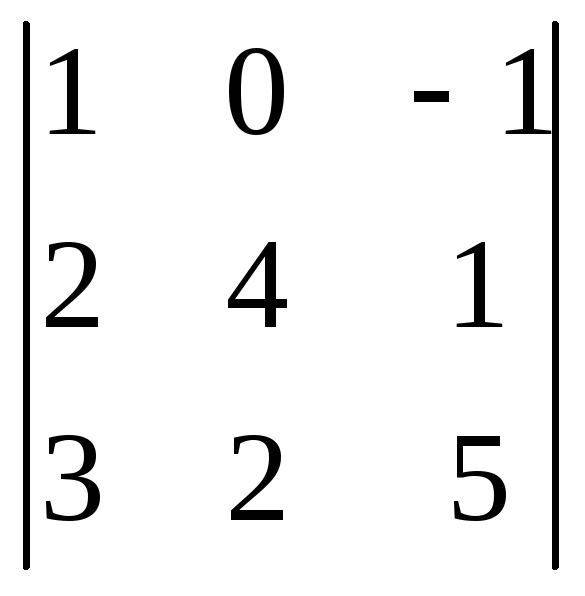различными способами.
Решение. 1-й способ. Используем правило треугольников:
.
2-й способ. Разложим определитель по первой строке:
.
3-й способ. Занулим элементы первой строки, то есть используем метод эффективного понижения порядка. Для этого прибавим к элементам 3-го столбца элементы 1-го столбца. Затем разложим определитель по 1-й строке: сложив соответствующие элементы 1-го и 3-го столбцов:
.
В. 7 Обратная матрица. Ранг матрицы
Пример 1.
Исследовать
матрицу A
на невырожденность, найти
если она существует, результат проверить:
.
Решение. Вычислим определитель матрицы A:
.
Невырожденность
матрицы A
означает, что существует единственная
обратная ей матрица
1-й способ. Используем формулу (4). Найдем алгебраические дополнения:
2-й способ.
Воспользуемся эквивалентностью матриц
и
.
Для этого используем элементарные
преобразования строк матрицы.
Тогда
по формуле (4) имеем
(5)
Тогда
Приходим к
заключению, что
имеет вид (5).
Для контроля
правильности результата достаточно
проверить условие
Действительно
В.8,9,10Системы линейных уравнений
Пример 1. Решить разными способами систему уравнений
Решение. 1-й способ. Используем метод обратной матрицы. Заданная система невырожденная, так как ее определитель не равен нулю. Действительно,
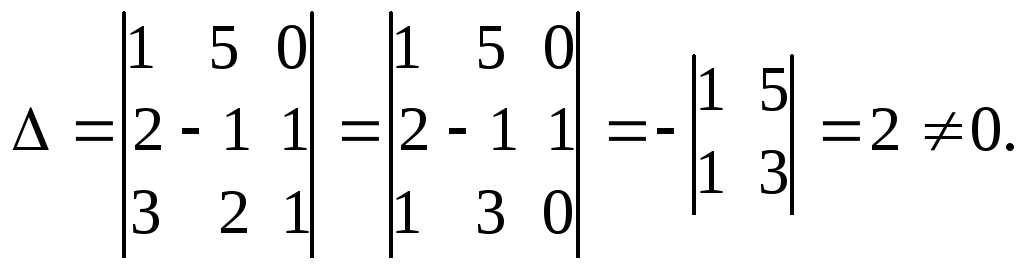(13)
Найдем обратную матрицу А–1. Вычисляем
А11 = –3; А21 = –5; А31 = 5;
А12 = 1; А22 = 1; А32 = –1;А13 = 7; А23 = 13; А33 = –12.
Следовательно,
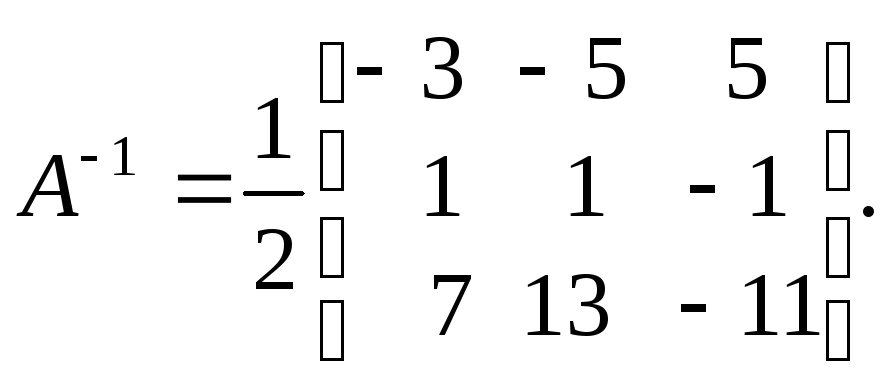
Используем далее формулу (10):
т. е. x1
= –2, x2
= 0, x3
= 8 – единственное решение. Получаем
ответ:
.
2-й способ. Используем формулы Крамера (11). Вычисляем определитель системы (13).
Заменяем в определителе первый столбец столбцом свободных членов и вычисляем
Заменяем в определителе второй столбец столбцом свободных членов и вычисляем
Заменяем в определителе третий столбец столбцом свободных членов. Тогда
Тогда, согласно формулам (11), имеем
Таким образом, получаем решение (–2; 0; 8).
3-й способ. Используем метод Гаусса. Приведем заданную систему к равносильной. Для этого осуществим элементарные преобразования строк расширенной матрицы системы:
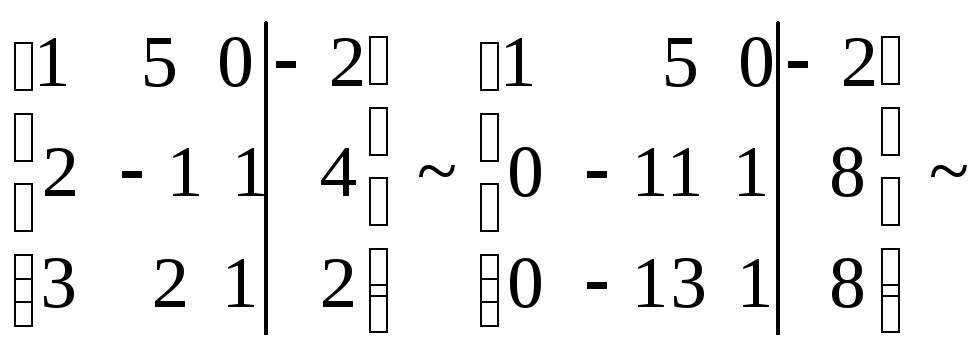
Последней матрице соответствует система
Из последней системы получаем
т.е пришли к ответу
Пример 2. Исследовать систему на совместность и найти ее решение:
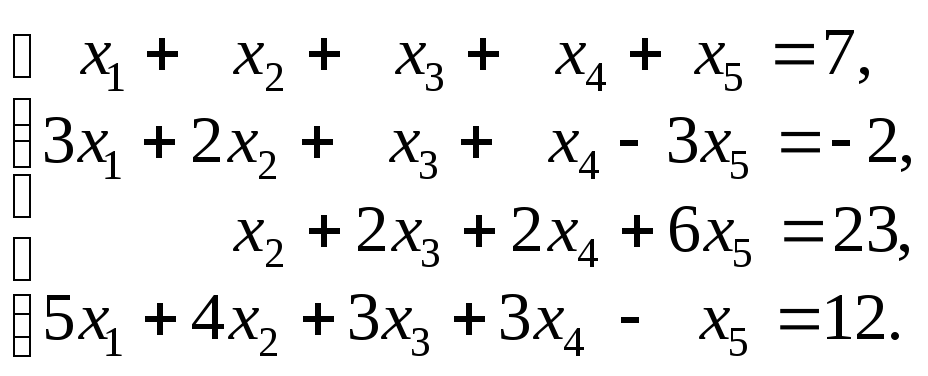
Решение. Запишем расширенную матрицу системы:
Наибольший порядок
отличных от нуля миноров равен 2 (так
как любой минор 3-го порядка содержит
нулевую строку, а, следовательно, будет
равен нулю). Значит,
и исходная система совместны.
Выберем в качестве
базисного минор
Тогда х1,
х2
– базисные неизвестные, х3,
х4,
х5
– свободные. Система,
равносильная исходной, имеет вид:
Полагаем х3 = с1, х4 = с2, х5 = с3,
где с1, с2, с3 – произвольные постоянные, и решаем указанную систему.
Получаем
Таким образом получаем множество решений вида
В 11. Векторы в пространстве: линейные операции над векторами в геометрической форме, проекция вектора на ось
Пример 1.
Векторы
и
неколлинеарны. Найти, при каком значении
векторы
и
будут коллинеарны.
Решение.
Условие
равносильно тому, что
где
некоторое
число, т. е.
откуда
Векторы
и
неколлинеарны, поэтому
Решая эту систему,
находим
и
или
Таким образом, при
имеем
Как легко видеть, выполняется
,
что и означает коллинеарность векторов
и
.
Пример 2.
Дана треугольная призма
(рис. 3). Разложить вектор
по векторам
и
Решение. По правилу треугольника имеем
Складывая левые и правые части этих векторных равенств, получаем
Так как
и
то
и, следовательно,
Рис. 3.
В.15 Линейная зависимость векторов. Действиянад векторами в координатной форме
Пример 1.
Даны векторы
в некотором базисе. Найти координаты
вектора
в этом базисе.
Решение.
Определим координаты вектора
следуя правилам действий над векторами
в координатной форме (см. формулы (2) и
(3)), т. е.
В
дальнейшем, если не оговорено противное,
все координаты считаются заданными в
ортонормированном базисе.
Пример 2.
Вычислить проекцию вектора
на направление вектора
Решение. Используем формулы (1), (4), (7):
Пример 3.
Найти направляющие косинусы вектора
Решение. Используем формулы (9):
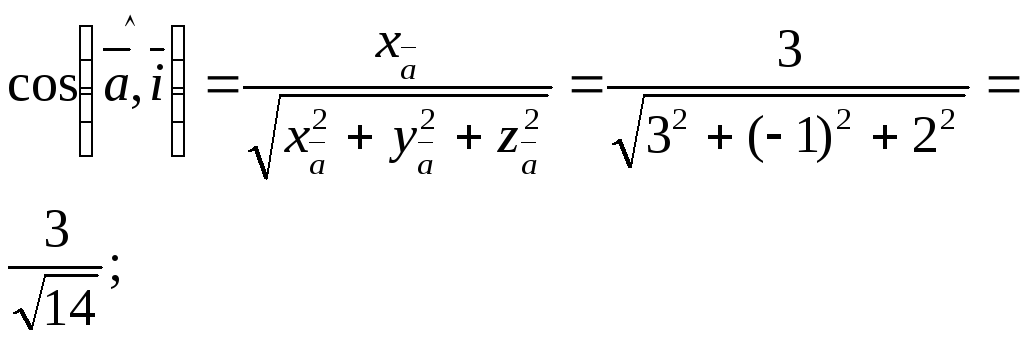
Пример 4.
Найти прямоугольные декартовы координаты
вектора
если
Решение.
Пусть
.
Используя определение координат вектора,
имеем
Получаем,
.
В.13 Векторное произведение
Пример 1.
Пусть
Найти:
1)
;
2)
;
3)
.
Решение.
1. По определению векторного произведения
векторов
и
его длина есть
2. Используя алгебраические свойства векторного произведения, имеем
Значит,
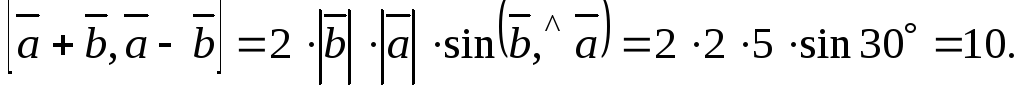
3. Используем свойства векторного произведения и условие задачи. Получим
Пример 2. Упростить выражение:
1)
;
2)
.
Решение.
Воспользуемся равенствами
,
которые верны по определению векторного
произведения и его свойствам. Тогда
1.
;
2.
Пример 3.
Вычислить площадь параллелограмма,
диагоналями которого служат векторы
и
где
Решение. Используем известную из планиметрии формулу площади параллелограмма и геометрический смысл векторного произведения:
,
где
Тогда, по свойствам векторного произведения
Пример 4.
Вычислить площадь
и его высоту, опущенную из вершины A
на сторону BC,
если A(1,
1, 1), B(4,
2, –1), C(2,
3, 0).
Решение.
где
– площадь параллелограмма, построенного
на векторах
и
.
Так как
,
то найдем сначала
.
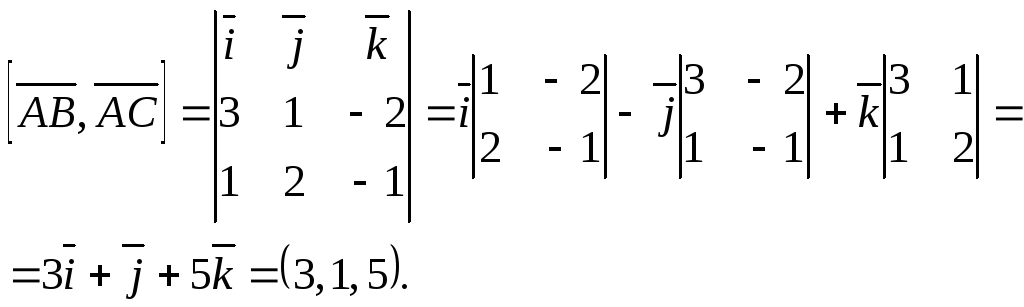
Тогда
Значит,
Для нахождения
высоты h
треугольника
воспользуемся формулой
из которой
Здесь
Значит,
Пример 5. Даны три силы:
,
,
,
приложенные к точке A(–1,
4, 2). Определить величину и направляющие
косинусы момента равнодействующей этих
сил относительно точки O(2,
3, –1).
Решение.
Пусть сила
равнодействующая
сил
.
Тогда
.
Значит, согласно физическому смыслу
векторного произведения, момент
этой силы равен
Вычисляем
.
Для нахождения направляющих косинусов
используем формулы (9):
