
11 Задание
Потоком вектора
 (x,y,z)=P(x,y,
(x,y,z)=P(x,y, z)
z) +Q(x,y,z)
+Q(x,y,z) +R(x.y,z)
+R(x.y,z) через кусочно-гладкую ориентированную
поверхностьS
называется интеграл от дивергенции
векторного поля F
, распространённый по некоторому объёму
Vdiv
через кусочно-гладкую ориентированную
поверхностьS
называется интеграл от дивергенции
векторного поля F
, распространённый по некоторому объёму
Vdiv dV=S
dV=S dS
dSПо определению, если функция (x,y,z) непрерывна на кусочно-гладкой поверхности S, то поверхностным интегралом первого рода называется предел последовательности интегральных сумм I=1(x,y,z)i при max i0 который не зависит ни от способа деления поверхности S ни от выбора точек PiS , его обозначение (x,y,z)d
По определению, если вектор-функция
 (x,y,z)=
P(x,y,z)
(x,y,z)=
P(x,y,z) +Q(x,y,z)
+Q(x,y,z) +R(x.y,z)
+R(x.y,z) (*) непрерывна на кусочно-гладкой
ориентированной поверхностиS,
то поверхностным интегралом второго
рода называется поток вектора (*) через
к., его обозначение Sφdxdy
(*) непрерывна на кусочно-гладкой
ориентированной поверхностиS,
то поверхностным интегралом второго
рода называется поток вектора (*) через
к., его обозначение SφdxdyНаправляющие косинусы нормали cos(
 ,
, ),cos(
),cos( ,
, ),cos(
),cos( ,
, )
к ориентированной поверхностиS:
z=f(x,y)
соответственно равны cos(
)
к ориентированной поверхностиS:
z=f(x,y)
соответственно равны cos( ,
, )=
)=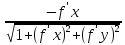 cos(
cos( ,
, )=
)= cos(
cos( ,
, )=
)=
Если функция R(x,y,z), непрерывна на кусочно-гладкой ориентированной поверхности S: z=f(x,y), (x,y)∈D (D - замкнутая ограниченная область), то SR(x,y,z)dxdy вычисляется по формуле: ±DxyR(x,y))dxdy
Масса кусочно-гладкой поверхности S с плотностью ρ(x,y,z), (x,y,z)∈S равна Sρ(x,y,z)dS
Если функция Q(x,y,z} непрерывна на кусочно-гладкой ориентированной поверхности S: у = g(x,z) ((x,z)∈D, D -замкнутая ограниченная область плоскости XOZ), то SQ(x, y,z)dxdz вычисляется по формуле: ±DQ(x,y(x,z),z))dxdz
По теореме о сведении поверхностного интеграла первого рода к двойному, если функция f(x,y,z) непрерывна на кусочно-гладкой поверхности S: z=z(x,y) ((x,y)∈D, D - замкнутая ограниченная область плоскости XОУ), то Sf(x,y,z)dS=Df(x,y,z(x,y))
 dxdy
dxdyПо определению, если вектор-функция
 (x,y,z)=P(x,y,z)
(x,y,z)=P(x,y,z) +Q(x,y,z)
+Q(x,y,z) +R(x.y,z)
+R(x.y,z) непрерывна на кусочно-гладкой
ориентированной поверхностиS,
то поверхностный
интеграл второго рода в векторной
форме имеет вид: Sφdxdy
непрерывна на кусочно-гладкой
ориентированной поверхностиS,
то поверхностный
интеграл второго рода в векторной
форме имеет вид: SφdxdyЕсли функция P(x,y,z) непрерывна на кусочно-гладкой ориентированной поверхности S: x=h(y,z) ((у,z)∈D, D- замкнутая ограниченная область плоскости YOZ), то SP(x,y,z)dydz равен ±DP(h(y,z),y,z))dydz
12 Задание
Если функции P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны на кусочно-гладкой ориентированной поверхности S с вектором нормали
 (cosα,cosβ,cosγ),
то S(Pcosα+Qcosβ+Rcosγ)ds
через
поверхностный интеграл второго рода
представляется в виде: SPdydz+Qdxdz+Rdxdy
(cosα,cosβ,cosγ),
то S(Pcosα+Qcosβ+Rcosγ)ds
через
поверхностный интеграл второго рода
представляется в виде: SPdydz+Qdxdz+RdxdyПо формуле Стокса циркуляция вектора
 (x,y,z)=P(x,y,
(x,y,z)=P(x,y, z)
z) +Q(x,y,z)
+Q(x,y,z) +R(x,y,z)
+R(x,y,z) по ориентированной кусочно-гладкой
замкнутой кривой Г, являющейся краем
поверхностиS,
равна
по ориентированной кусочно-гладкой
замкнутой кривой Г, являющейся краем
поверхностиS,
равна
 dl=Srot
dl=Srot dS,
где rot
dS,
где rot =
= x
x =
=
Формула Остроградского-Гаусса в векторной форме имеет вид: Vdiv
 dV=S
dV=S dS,
где
dS,
где
 =P
=P +Q
+Q +R
+R
Для вектора
 (x,y,z)=P(x,y,
(x,y,z)=P(x,y, z)
z) +Q(x,y,z)
+Q(x,y,z) +R(x,y,z)
+R(x,y,z) дивергенцией
называется div
дивергенцией
называется div =
= +
+ +
+
Формула Стокса в векторной форме имеет вид:
 dl=Srot
dl=Srot dS
dSЕсли функции P(x,y,z), Q(x,y,z) и R(x,y,z) непрерывны на кусочно-гладкой ориентированной поверхности S, то SP(x,y,z)dydz+Q(x,у,z)dzdx+R(x,у,z)dxdy через поверхностный интеграл первого рода представляется в виде: S(P(x,y,z)cosα+Q(x,у,z)cosβ+R(x,у,z)cosγ)dS
По формуле Остроградского-Гаусса поток вектор-функции
 (x,y,z)=P(x,y,
(x,y,z)=P(x,y, z)
z) +Q(x,y,z)
+Q(x,y,z) +R(x,y,z)
+R(x,y,z) через замкнутую поверхностьS,
ограничивающую область V,
в направлении внешней нормали равен
Vdiv
через замкнутую поверхностьS,
ограничивающую область V,
в направлении внешней нормали равен
Vdiv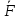 dV=S
dV=S dS,
где div
dS,
где div =
= +
+ +
+
Ротором (вихрем) вектора
 (x,y,z)=P(x,y,
(x,y,z)=P(x,y, z)
z) +Q(x,y,z)
+Q(x,y,z)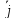 +R(x,y,z)
+R(x,y,z) называется вектор В определяемый
проекциямиBx=
называется вектор В определяемый
проекциямиBx= -
- ,By=
,By= -
- ,Bz=
,Bz= -
- , обозначаетсяrot
, обозначаетсяrot

По формуле Остроградского-Гаусса интеграл от дивергенции вектор-функции
 (x,y,z)=P(x,y,
(x,y,z)=P(x,y, z)
z) +Q(x,y,z)
+Q(x,y,z) +R(x,y,z)
+R(x,y,z) ,
непрерывной
в замкнутой области
,
непрерывной
в замкнутой области
 ,
ограниченной
замкнутой ориентированной поверхностью
S,
равен
Vdiv
,
ограниченной
замкнутой ориентированной поверхностью
S,
равен
Vdiv dV=S
dV=S dS,
где
div
dS,
где
div =
= +
+ +
+
По формуле Стокса поток вектора rot
 (
( (x,y,z)=P(x,y,
(x,y,z)=P(x,y, z)
z)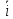 +Q(x,y,z)
+Q(x,y,z) +R(x,y,z)
+R(x,y,z) )
через поверхностьS
с краем Г, являющимся кусочно-гладкой
ориентированной замкнутой кривой,
равен S
rot
)
через поверхностьS
с краем Г, являющимся кусочно-гладкой
ориентированной замкнутой кривой,
равен S
rot dS=
dS= dl,
где rot
dl,
где rot =
= x
x =
=
