9 Задание

1. Статический момент M_OY относительно оси OY кусочно-гладкой кривой АВ с плотностью (х,у) вычисляется по формуле: M_OY=_ABx(x,y)dl

2. Момент инерции относительно начала координат кусочно-гладкой кривой АВ с плотностью (х,у) вычисляется по формуле: I_O=_AB(x²+y²)(x,y)dl

3. Момент инерции I_OY относительно оси ОY кусочно-гладкой кривой АВ с плотностью (х,у) вычисляется по формуле: I_OY=_ABx²(x,y)dl

4. Координаты ицентра масс кусочно-гладкой кривой АВ с плотностью (х,у), (х,у) АВ вычисляются по формулам: 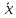=M_y/M=(_ABx(x,y)dl) / (_AB(x,y)dl) , =M_x/M=(_ABy(x,y)dl) / (_AB(x,y)dl)

5. Момент инерции J_OX относительно оси ОХ кусочно-гладкой кривой АВ с плотностью (х,у) вычисляется по формуле : J_OX=_ABy²(x,y)dl

6. Если f(x,y) и |f(x,y)| интегрируемы на кусочно-гладкой кривой АВ и I₁=|_AB(x,y)dl|, I₂=_AB|(x,y)|dl, то 1 I₁ I₂

7. По свойству аддитивности, если (x,y) интегрируема на кусочно-гладкой кривой АВ, точка САВ, то _AB(x,y)dl равен сумме интегралов вида: _AC(x,y)dl+_CB(x,y)dl

8. Масса кусочно-гладкой кривой AB по заданной плотности (х,у), (х,у)АВ вычисляется по формуле: m=_AB(x,y)dl

9. Статический момент Mx относительно оси OX кусочно-гладкой кривой АВ с плотностью (х,у), (х,у)АВ вычисляется по формуле: Mx=_ABy(x,y)dl

10. Если неотрицательная функция f(x,y) интегрируема на кусочно-гладкой кривой АВ, то для I=_AB(x,y)dl справедливо, 3 I  0

10 Задание

1. Для функций Р(х,у) и Q(x,y), непрерывных вместе с производным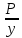и ив замкнутой областиG, ограниченной кусочно-гладкой ориентированной кривой L, формула Грина имеет вид: _G(Q/x-)dxdy

2. Если Р(х,у) и Q(x,y)-непрерывные функции в односвязной области G и (x,y)dx+Q(x,y)dy=0 (L-произвольный ориентированный замкнутый контур из G), то для любых точек А и В из G интеграл _ABP(x,y)dx+Q(x,y)dy не зависит от пути интегрирования , а зависит только от расположения т.А и т.В

3. С помощью криволинейного интеграла площадь области G, ограниченной кусочно-гладкой ориентированной кривой L, вычисляется по формуле: S=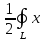dy-ydx

4. Если P(x,y) и Q(x,y) - непрерывные функции в односвязной области G и P(x,y)dx+Q(x,y)dy=dU(x,y) (U(x,y) - функция, определенная в G), то для любых точек A и В из G _ABP(x,y)dx+Q(x,y)dy не зависит от пути интегрирования , а зависит только от расположения т.А и т.В

5. Если P(x,y) непрерывна вместе с в замкнутой области G, ограниченной кусочно-гладкой кривойL, то _Gdxdy равен S= -(x,y)dx

6. Если фу-ии Р(х,у) и Q(х,y) непрерывны вместе с ив односвязной областиG и =, то для любых т. А и В изG _ABPdx+Qdy не зависит от пути интегрир-ния, а зависит только от расположения т.А и т.В

7. Если функции P(x,y) и Q(х,y) -непрерывны в односвязной области G и для любых точек А и В _ABP(x,y)dx+Q(x,y)dy не зависит от пути интегрирования, то существует функция U(x,y), определенная в G такая, что Pdx + Qdy есть полный дифференциал функции U(x,y)

8. Если функции P(x,y) и Q(x,y) - непрерывны в односвязной области с кусочно-гладкой ориентированной границей Г и для любых точек А и В изG _ABP(x,y)dx+Q(x,y)dy не зависит от пути интегрирования, а I=(x,y)dx+Q(x,y)dy то 2 I=0

9. Если Q(x,y) непрерывна вместе с в замкнутой области G , ограниченной кусочно-гладкой кривойL, то _Gdxdy равен (x,y)dy

10. Если Р(х,у) и Q(x,y) непрерывны вместе с ив односвязной областиG и для любых точек А и В из G _ABP(x,y)dx+Q(x,y)dy не зависит от пути интегрирования, то 1 =