3 Задание

1. По свойству линейности, если функции f(x,y,z) и g(x,y,z) интегрируемы на V, то для любых чисел A и В интеграл _v(A+Bg)dV равен A_vdV+B_vgdV

2. По свойству аддитивности, если области V, V₁ и V₂ такие, что V₁V, V₂=V\и функция(x,y,z) интегрируема на V , то  интегрbhetvf на V₁ и V₂ причём _V(x,y,z)dV равен _V1(x,y,z)dV+_V2(x,y,z)dV

3. По свойству монотонности тройного интеграла, если функции (x,y,z) и g(x,y,z) интегрируемы на V и (x,y,z)g(x,y,z) на V, то _V(x,y,z)dV_Vg(x,y,z)dV

4. По свойству тройного интеграла, если (x,y,z) и |(x,y,z)| интегрируемы на V ,то для |_VdV| и _V||dV выполняется неравенство |_VdV|_V||dV

5. По свойству об оценке тройного интеграла, если (x,y,z) интегрируема на V и mM (m,M - const) , то выполняется неравенство _VmdV_V(x,y,z)dV_VMdV

6. По свойству линейности, если функции (x,y,z) и g(x,y,z) интегрируемы на V, тогда для любых чисел A и B сумма A_VdV+B_VgdV равна _V(A+Bg)dV

7. По теореме о сведении тройного интеграла к повторному, если функция (x,y,z) - интегрируема на V , где V={(x,y,z):(x,y)z(x,y), (x,y)G} (G – проекция V) , то интеграл _V(x,y,z)dV равен _Gdxdy_(x,y)^(x,y)(x,y,z)dz

8. По свойству монотонности для тройного интеграла, если функция (x,y,z) – неотрицательна и интегрируема на VR³ , то выполняется неравенство _V(x,y,z)dV0

9. По свойству аддитивности, если области V, V₁ и V₂ такие, что V₁V, V₂=V\и функция(x,y,z) интегрируема на V , то  интегрируема на V₁ и V₂, причём сумма _V1dV+ _V2dV равна _VdV

10. Если функции (x,y,z) и g(x,y,z) интегрируемы на V, (x,y,z)g(x,y,z) на V и A=_V(x,y,z)dV, B=_Vg(x,y,z)dV, то справедливо соотношение: 2 AВ

4 Задание

1. Если формулы x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) задают взаимно однозначное, непрерывно дифференцируемое отображение области Т пространства переменных (u,v,w) на область  пространства переменных (x,y,z), то якобиан отображения l(u,v,w) равен I= 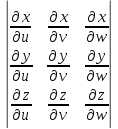=(x,y,z)

2. Если отображение области D плоскости переменных (r,) на область G плоскости переменных (x,y) определяется полярными координатами r и , то _G(x,y)dxdy= _D(rcos,rsin)rdrd

3. Якобиан J(r,,) отображения, определяемого сферическими координатами r,,, равен определителю

I= ==r²cos

4. Если формулы x=x(u,v), y=y(u,v) задают взаимно однозначное и непрерывно дифференцируемое отображение области D плоскости переменных (u,v) на область G плоскости переменных (x,y) , то _G(x,y)dxdy= _D(x(u,v), y(u,v))I(u,v)dudv где якобиан I(u,v) равен I(u,v)=

5. Якобиан J(r,, z) отображения, определяемого цилиндрическими координатами r,,z, равен определителю J(r,,z)====r

6. Если формулы x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) задают взаимно однозначное и непрерывно дифференцируемое отображение области Т пространства переменных (u,v,w) на область  пространства переменных (x.y,z), то _dxdydz=_T(x,y,z)Idudvdw , где якобиан I(u,v,w) равен=(x,y,z)

7. Если отображение области Т пространства переменных (r,,) на область  пространства переменных (x,y,z) определяется сферич-ми корд-тами, то _f(x,y,z)dxdydz=_T(rcoscos,rcossin ,rsin)r²cosdrdd

8. Если формулы x=x(u,v), у=y(u.v) задают взаимно однозначное и непрерывно дифференцируемое отображение области D плоскости переменных (u,v) на область G плоскости переменных (х,у), то якобиан I(u,v) отображения равен

9. Если отображение области Т пространства переменных (r, , z) на область  пространства переменных (x, y, z) определяется цилиндрическими координатами, то _(x,y,z)dxdydz=_T(rcos, rsin,z)rdrddz

10. Если функции x=x(u,v,w), y=y(u,v,w), z=z(u,v,w) задают взаимно однозначное и непрерывно дифференцируемое отображение области Т пространства переменных (u,v,w) на область  пространства переменных (x,y,z), и якобиан отображения I(u.v.w) равен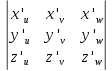, то_(x,y,z)dxdydz=_T(x(u,v,w), y(u,v,w), z(u,v,w))I(u,v,w)dudvdw