
1Задание
Двойным интегралом от функции (x,y) , непрерывной в замкнутой области GR2 , называется
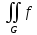 (x,y)dxdy,
предел интегр-ой суммы
(x,y)dxdy,
предел интегр-ой суммы
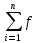 (xi,yi)·∆Si
когда n→∞,
т.о. ∃maxdi→0
(xi,yi)·∆Si
когда n→∞,
т.о. ∃maxdi→0
 (xi,yi)dSi
(xi,yi)dSiС помощью двойного интеграла объём тела V={(x,y,z):f(x,y)≤z≤0, (x,y)G} записывается в виде: V=
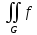 (x,y)dxdy
(x,y)dxdyЕсли функция (x,y), ((x,y)G) – плотность распределения масс, то физический смысл интеграла
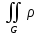 (x,y)dxdy
есть масса плоской пластинки G.
(x,y)dxdy
есть масса плоской пластинки G.Геометрический смысл интеграла
 V
есть объём области V
V
есть объём области V
Интеграл
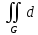 G
равен площади области G.
G
равен площади области G.Тройным интегралом от функции f(x,y,z), непрерывной в замкнутой области
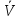 ,
называется предел последовательности
интегральных сумм
,
называется предел последовательности
интегральных сумм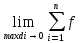 (xi,yi,zi)∆Vi
(xi,yi,zi)∆ViЕсли f(x,y) – неотрицательная интегрируемая функция в области G, то геометрический смысл
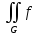 (x,y)dxdy
есть объём цилиндрического тела с
основанием G
,с образующими ∥
оси OZ
и ограниченной сверху поверхностью
z=(x,y)
(x,y)dxdy
есть объём цилиндрического тела с
основанием G
,с образующими ∥
оси OZ
и ограниченной сверху поверхностью
z=(x,y)Если функция (x,y,z), (x,y,z)V, - плотность распределения масс, то физический смысл интеграла
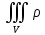 (x,y,z)
есть масса неоднородного тела с
плотностью (x,y,z)
в т.М(x,y,z)
(x,y,z)
есть масса неоднородного тела с
плотностью (x,y,z)
в т.М(x,y,z)Масса пластинки GR2 с плотностью (x,y), (x,y)G равна
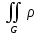 (x,y)dxdy
(x,y)dxdyПлощадь области GXOY равна
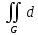 xdy
xdy
2 Задание
Если функции f(x,y) и g(x,y) интегрируемы на G, f(x,y)≤g(x,y) на G и
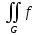 dG=A,
а
dG=A,
а
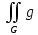 dG=B,
то 2
A
B
dG=B,
то 2
A
BПо теореме о сведении двойного интеграла к повторному, если функция (x,y) интегрируема на G, где G={(x,y):φ(x)≤y≤ψ(x), a≤x≤b}, то
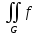 (x,y)dG
равен
(x,y)dG
равен
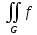 (x,y)dxdy=
(x,y)dxdy= (x,y)dy]dx
(x,y)dy]dxПо свойству линейности, если функции f(x,y) и g(x,y) интегрируемы на G, тогда для любых чисел A и B сумма A
 dG+B
dG+B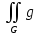 dG
равна
dG
равна
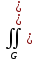 Af+Bg)dG
Af+Bg)dGПо свойству аддитивности , если области G, G1 и G2 такие, что G1G, G2=G\
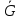 1,
а функция f(x,y)
интегрируема на G,
то f
интегрируема на G1
и G2
причём
1,
а функция f(x,y)
интегрируема на G,
то f
интегрируема на G1
и G2
причём
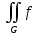 dG
равен
dG
равен
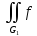 dG+
dG+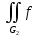 dG
dGПо свойству линейности, если функции f(x,y,z) и g(x,y,z) – интегрируемы на V, тогда для любых чисел A и B интеграл
 Af+Bg)dV
равен A
Af+Bg)dV
равен A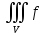 dV+B
dV+B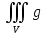 dV
dVПо свойству монотонности тройного интеграла, если функция f(x,y,z) неотрицательна и интегрируема на G, то выполняется неравенство
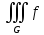 (x,y,z)dxdydz≥0
(x,y,z)dxdydz≥0По свойству монотонности двойного интеграла, если функции f(x,y) и g(x,y) интегрируемы на G и f(x,y) ≤g(x,y) на G, то
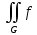 (x,y)dxdy≤
(x,y)dxdy≤ (x,y)dxdy
(x,y)dxdyПо свойству аддитивности, если области G, G1 и G2 такие, что G1G, G2=G\
 и функция(х,у)
- интегрируема в G,
то (x,y)
интегрируема на G1
и G2,
причем сумма
и функция(х,у)
- интегрируема в G,
то (x,y)
интегрируема на G1
и G2,
причем сумма
 dG+
dG+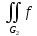 dG
равна
dG
равна
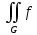 dG
dGПо свойству об оценке двойного интеграла, если f(x,y) интегрируема на G и m f M (m,M-const), то выполняется неравенство
 dxdy≤
dxdy≤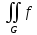 (x,y)dxdy≤
(x,y)dxdy≤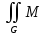 dxdy
dxdyПо свойству двойного интеграла, если f(x,y) и |f(x,y)| интегрируемы на G, то для |
 dG|
и
dG|
и
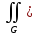 f|dG
выполняется неравенство |
f|dG
выполняется неравенство |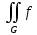 dG|≤
dG|≤ f|dG
f|dG
