2.3.2Проверка гипотезы о значении математического ожидания нормальной случайной величины с неизвестной дисперсией (одновыборочный t-критерий)

Пример 1.

На основе данных о значениях игровых показателей игроков НБА за сезон 2011/2012г, проверим на уровне значимости гипотезу H0: μ=μ0. Средний уровень по максимуму очков у выборочной группы и у всего объема выбранных игроков равен.

Результат представлен на листе Excel «Одновыб. t-критерий 1», а также на рисунке 2.13.

Рисунок 2.13. Одновыборочный t-критерий, пример 1

Полученный результат свидетельствует о том, что гипотеза H₀: противоречит данным эксперимента. К такому же выводу приводит и сравнение значимости с заданным уровнем значимости , .

2.3.3Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с известными дисперсиями (двухвыборочный z-критерий)

На основе данных о значениях игровых показателей игроков НБА за сезон 2011/2012г, используя процедуру Двухвыборочный z-тест, проверим на уровне значимости гипотезу H0: μ1=μ2. Генеральные средние μ1 и μ2 максимума очков и среднего количества очков за игру у всего объема выбранных игроков равны.. Альтернативная гипотеза H₁: .

Результат представлен на листе Excel «Двухвыб. z-критерий», а также на рисунке 2.15.

Рисунок 2.15. Двухвыборочный z-критерий

Анализ результатов решения свидетельствует о том, что расчетное значение статистики находится в области принятия гипотезы . Это означает, что гипотеза H₀: о равенстве средних не противоречит фактическим данным наблюдения и, следовательно, её надо принять. К такому же выводу приводит и сравнение значимости с заданным уровнем значимости , .

2.3.4Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с равными неизвестными дисперсиями (двухвыборочный t-критерий, равные дисперсии)

На основе данных о значениях игровых показателей игроков НБА за сезон 2011/2012г, используя процедуру Двухвыборочный t-тест с одинаковыми дисперсиями, проверим на уровне значимости гипотезу H₀: о том, что средние числа равны. Альтернативная гипотеза H₁: .

Результат представлен на листе Excel «Двухвыб. t-крит., рав. д.», а также на рисунке 2.16.

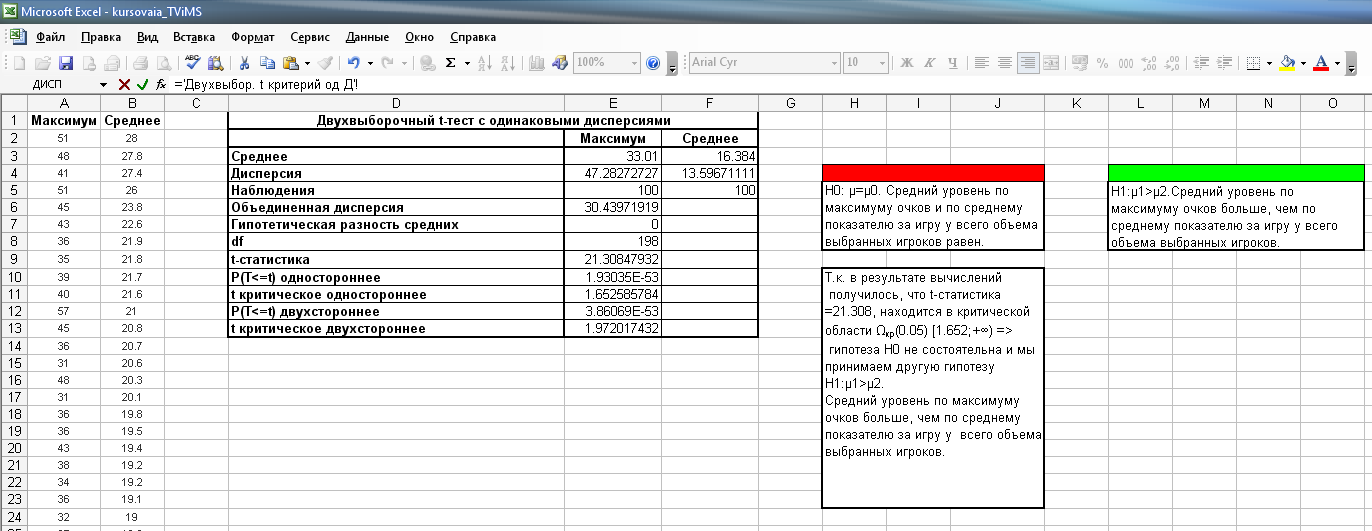
Рисунок 2.16. Двухвыборочный t-критерий, равные дисперсии

Анализ результатов решения свидетельствует о том, что расчетное значение t-статистики находится вне области принятия гипотезы . Это означает, что гипотеза H₀: о равенстве средних противоречит фактическим данным наблюдения и, следовательно, её надо отклонить (на уровне значимости ) и принять альтернативную гипотезу H₁: . К такому же выводу приводит и сравнение значимости с заданным уровнем значимости , .

2.3.5Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с различными неизвестными дисперсиями (двухвыборочный t-критерий, различные дисперсии)

На основе данных о значениях игровых показателей игроков НБА за сезон 2011/2012г, используя процедуру Двухвыборочный t-тест с различными дисперсиями, проверим на уровне значимости гипотезу H₀: о том, что средние равны. Альтернативная гипотеза H₁: .

Результат представлен на листе Excel «Двухвыб. t-крит., разл. д.», а также на рисунке 2.17.

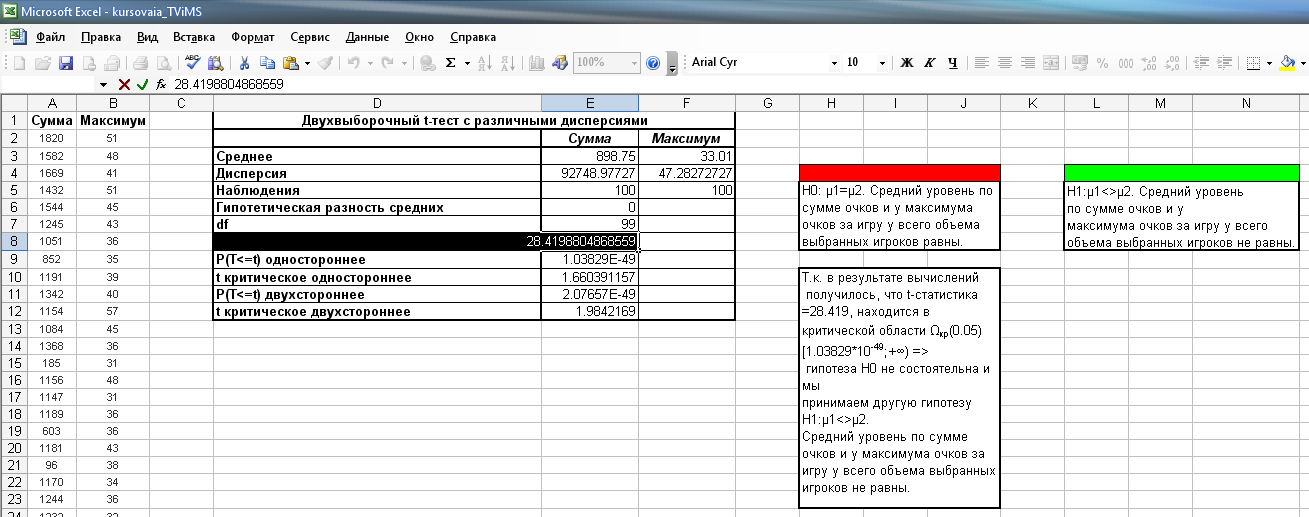
Рисунок 2.17. Двухвыборочный t-критерий, различные дисперсии

Анализ результатов решения свидетельствует о том, что расчетное значение t-статистики находится вне области принятия гипотезы . Это означает, что гипотеза H₀: о равенстве средних температур противоречит фактическим данным наблюдения и, следовательно, её надо отклонить (на уровне значимости ) и принять альтернативную гипотезу H₁: . К такому же выводу приводит и сравнение значимости с заданным уровнем значимости , , т.е. .