1.2.2Функция ранг
Функция РАНГ в Excel вычисляется по следующей формуле:
РАНГ (число; массив; порядок), (18)
где число – элемент выборки, ранг которого надо определить; массив – массив или диапазон ячеек, содержащий элементы исследуемой случайно выборки (неупорядоченные данные наблюдения); порядок – величина, определяющая, как упорядочивать (ранжировать) массив.
1.3Проверка параметрических гипотез
Под статистической гипотезой принято понимать любое (разумное с точки зрения теории вероятности) предположение о закономерностях, которым подчиняется исследуемый случайный объект (случайное событие, случайная величина, система случайных величин или случайная функция). Статистическую гипотезу принято обозначать символом H.
Параметрической гипотезой называется определенное предположение о значении параметра (числовой характеристики) исследуемого случайного объекта. Параметрические гипотезы проверяются с помощью статистических критериев, называемых параметрическими критериями.
1.3.1Проверка гипотезы о значении математического ожидания нормальной случайной величины с известной дисперсией (одновыборочный z-критерий)
Для проверки
гипотезы H0:
о том, что математическое ожидание
(среднее)
нормальной случайной величины
с известной дисперсией
равно заданному числу
,
используется статистика
, (19)
где
– выборочная оценка математического
ожидания
нормальной случайной величины
;
– объем выборки.
1.3.2Проверка гипотезы о значении математического ожидания нормальной случайной величины с неизвестной дисперсией (одновыборочный t-критерий)
Для проверки гипотезы H0: о том, что среднее нормальной случайной величины равно заданному числу , используется статистика, называемая отношением Стьюдента:
, (20)
где
– объем выборки;
и
– выборочные оценки среднего
и стандартного отклонения
нормальной случайной величины
.
1.3.3Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с известными дисперсиями (двухвыборочный z-критерий)
При проверке
гипотезы H0:
о том, что разность между математическими
ожиданиями
и
независимых нормальных величин
и
с известными дисперсиями
и
равна заданному числу
,
используется статистика
, (21)
где
и
– выборочные оценки математических
ожиданий исследуемых нормальных
случайных величин
и
;
– гипотетическое значение разности
математических ожиданий этих случайных
величин;
и
– объемы выборок, по которым проверяется
гипотеза H0.
1.3.4Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с равными неизвестными дисперсиями (двухвыборочный t-критерий, равные дисперсии)
При проверке гипотезы H0: о том, что разность между математическими ожиданиями и независимых нормальных величин и с известными дисперсиями и равна заданному числу , используется статистика
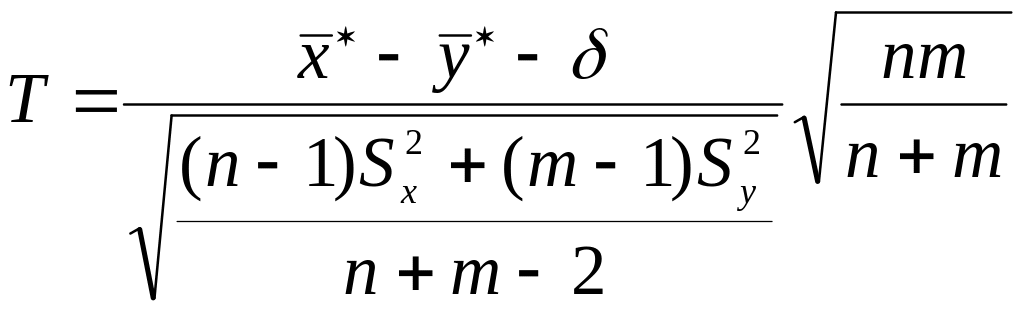, (22)
где
;
;
;
– выборочные оценки математических
ожиданий и дисперсий исследуемых
нормальных случайных величин
и
;
– гипотетическое значение разности
математических ожиданий этих случайных
величин;
и
– объемы выборок, по которым проверяется
гипотеза.
1.3.5Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с различными неизвестными дисперсиями (двухвыборочный t-критерий, различные дисперсии)
При проверке гипотезы H0: о том, что разность между математическими ожиданиями и независимых нормальных величин и с различными неизвестными дисперсиями равна заданному числу , используется статистика Фишера-Беренса
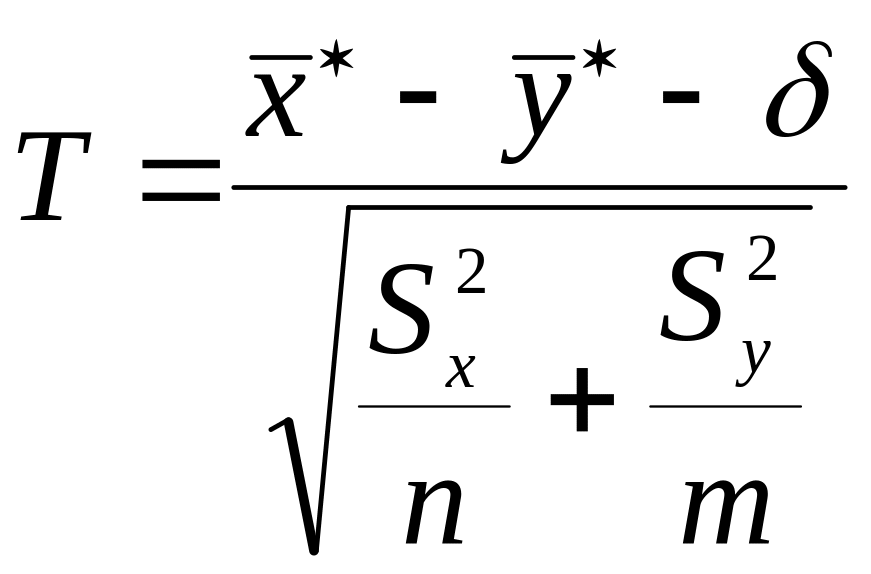, (23)
где ; ; ; – выборочные оценки математических ожиданий и дисперсий исследуемых нормальных случайных величин и ; – гипотетическое значение разности математических ожиданий этих случайных величин; и – объемы выборок, по которым проверяется гипотеза H0.