
- •Введение
- •1Теоретическая часть
- •1.1Первичная обработка статистических данных
- •1.1.1Исходные данные
- •1.1.2Упорядочение данных наблюдения
- •1.1.3Способ равных интервалов
- •1.1.4Способ равных частот
- •1.1.5Группировка данных наблюдения над дискретной случайной величиной
- •1.2Порядковые статистики и ранги
- •1.2.1Статистическая процедура “Ранг и персентиль”
- •1.2.2Функция ранг
- •1.3Проверка параметрических гипотез
- •1.3.1Проверка гипотезы о значении математического ожидания нормальной случайной величины с известной дисперсией (одновыборочный z-критерий)
- •1.3.2Проверка гипотезы о значении математического ожидания нормальной случайной величины с неизвестной дисперсией (одновыборочный t-критерий)
- •1.3.3Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с известными дисперсиями (двухвыборочный z-критерий)
- •1.3.4Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с равными неизвестными дисперсиями (двухвыборочный t-критерий, равные дисперсии)
- •1.3.5Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с различными неизвестными дисперсиями (двухвыборочный t-критерий, различные дисперсии)
- •1.3.6Проверка гипотезы о разности математических ожиданий двух кореллированных нормальных случайных величин с неизвестными дисперсиями (двухвыборочный t-критерий, сопряженные пары наблюдений)
- •1.4Проверка гипотезы о законе распределения случайной величины (критерии согласия)
- •1.4.1Критерий согласия хи-квадрат Пирсона
- •1.4.2Критерий согласия Колмогорова
- •1.4.3Критерий Крамера-Мизеса-Смирнова
- •1.4.4Критерий Андерсона-Дарлинга
- •1.4.5Критерии w Шапиро-Уилка
- •2.1.6Эмпирическая функция распределения
- •2.1.7Эмпирическая плотность вероятности
- •2.1.8Эмпирический ряд распределения
- •2.1.9Статистическая процедура «Описательная статистика»
- •2.3.2Проверка гипотезы о значении математического ожидания нормальной случайной величины с неизвестной дисперсией (одновыборочный t-критерий)
- •2.3.3Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с известными дисперсиями (двухвыборочный z-критерий)
- •2.3.4Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с равными неизвестными дисперсиями (двухвыборочный t-критерий, равные дисперсии)
- •2.3.5Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с различными неизвестными дисперсиями (двухвыборочный t-критерий, различные дисперсии)
- •2.3.6Проверка гипотезы о равенстве дисперсий двух независимых нормальных случайных величин (f-критерий)
- •2.3.7Проверка гипотезы о равенстве дисперсий нескольких независимых нормальных случайных величин (критерии Бартлета и Кокрена)
- •2.4Проверка гипотезы о законе распределения случайной величины (критерии согласия)
- •2.4.1Критерий согласия хи-квадрат Пирсона
- •2.4.2Критерий согласия Колмогорова
- •2.4.3Критерий Крамера-Мизеса-Смирнова
- •2.4.4Критерий Андерсона-Дарлинга
- •2.4.5Критерии w Шапиро-Уилка
- •Заключение
- •Список литературы
- •Приложение а

Содержание
Введение 6
1 Теоретическая часть 7
1.1 Первичная обработка статистических данных 7
1.1.1 Исходные данные 7
1.1.2 Упорядочение данных наблюдения 7
1.1.3 Способ равных интервалов 8
1.1.4 Способ равных частот 8
1.1.5 Группировка данных наблюдения над дискретной случайной величиной 10
1.1.6 Эмпирическая функция распределения 10
1.1.7 Эмпирическая плотность вероятности 10
1.1.8 Эмпирический ряд распределения 11
1.1.9 Статистическая процедура «Описательная статистика» 11
1.2 Порядковые статистики и ранги 12
1.2.1 Статистическая процедура “Ранг и персентиль” 12
1.2.2 Функция РАНГ 13
1.3 Проверка параметрических гипотез 13
1.3.1 Проверка гипотезы о значении математического ожидания нормальной случайной величины с известной дисперсией (одновыборочный z-критерий) 13
1.3.2 Проверка гипотезы о значении математического ожидания нормальной случайной величины с неизвестной дисперсией (одновыборочный t-критерий) 14
1.3.3 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с известными дисперсиями (двухвыборочный z-критерий) 14
1.3.4 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с равными неизвестными дисперсиями (двухвыборочный t-критерий, равные дисперсии) 15
1.3.5 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с различными неизвестными дисперсиями (двухвыборочный t-критерий, различные дисперсии) 15
1.3.6 Проверка гипотезы о разности математических ожиданий двух кореллированных нормальных случайных величин с неизвестными дисперсиями (двухвыборочный t-критерий, сопряженные пары наблюдений) 16
1.3.7 Проверка гипотезы о значении дисперсии нормальной случайной величины 16
1.3.8 Проверка гипотезы о равенстве дисперсий двух независимых нормальных случайных величин (F-критерий) 17
1.3.9 Проверка гипотезы о равенстве дисперсий двух кореллированных нормальных случайных величин 17
1.3.10 Проверка гипотезы о равенстве дисперсий нескольких независимых нормальных случайных величин (критерии Бартлета и Кокрена) 18
1.4 Проверка гипотезы о законе распределения случайной величины (критерии согласия) 19
1.4.1 Критерий согласия хи-квадрат Пирсона 19
1.4.2 Критерий согласия Колмогорова 19
1.4.3 Критерий Крамера-Мизеса-Смирнова 20
1.4.4 Критерий Андерсона-Дарлинга 20
1.4.5 Критерии W Шапиро-Уилка 20
2 Практическая часть 22
2.1 Первичная обработка статистических данных 22
2.1.1 Исходные данные 22
2.1.2 Упорядочение данных наблюдения 24
2.1.3 Способ равных интервалов 24
2.1.4 Способ равных частот 25
2.1.5 Группировка данных наблюдения над дискретной случайной величиной 26
2.1.6 Эмпирическая функция распределения 27
2.1.7 Эмпирическая плотность вероятности 28
2.1.8 Эмпирический ряд распределения 29
2.1.9 Статистическая процедура «Описательная статистика» 30
2.2 Порядковые статистики и ранги 31
2.2.1 Статистическая процедура “Ранг и персентиль” 31
2.2.2 Функция РАНГ 32
2.3 Проверка параметрических гипотез 32
2.3.1 Проверка гипотезы о значении математического ожидания нормальной случайной величины с известной дисперсией (одновыборочный z-критерий) 32
2.3.2 Проверка гипотезы о значении математического ожидания нормальной случайной величины с неизвестной дисперсией (одновыборочный t-критерий) 33
2.3.3 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с известными дисперсиями (двухвыборочный z-критерий) 34
2.3.4 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с равными неизвестными дисперсиями (двухвыборочный t-критерий, равные дисперсии) 35
2.3.5 Проверка гипотезы о разности математических ожиданий двух независимых нормальных случайных величин с различными неизвестными дисперсиями (двухвыборочный t-критерий, различные дисперсии) 36
2.3.6 Проверка гипотезы о равенстве дисперсий двух независимых нормальных случайных величин (F-критерий) 37
2.3.7 Проверка гипотезы о равенстве дисперсий нескольких независимых нормальных случайных величин (критерии Бартлета и Кокрена) 39
2.4 Проверка гипотезы о законе распределения случайной величины (критерии согласия) 42
2.4.1 Критерий согласия хи-квадрат Пирсона 42
2.4.2 Критерий согласия Колмогорова 44
2.4.3 Критерий Крамера-Мизеса-Смирнова 45
2.4.4 Критерий Андерсона-Дарлинга 46
2.4.5 Критерии W Шапиро-Уилка 46
Заключение 51
Список литературы 52
Приложение А 53
Введение
Данная работа посвящена изучению средств обработки выборочных данных статистическими методами.
В курсовой работе рассмотрены встроенные средства статистического анализа табличного процессора Excel. Теоретическая часть включает в себя краткое изложение основных понятий теоретической и прикладной статистики, описание технологии использования Excel при решении практических задач анализа данных. Практическая часть включает в себя примеры использования Excel при решении задач анализа данных.
В качестве статистических данных взяты значения игровых показателей игроков НБА за сезон 2011/2012г.
1Теоретическая часть
1.1Первичная обработка статистических данных
1.1.1Исходные данные
Любое статистическое исследование начинается со сбора данных об исследуемом случайном объекте. Таким объектом может быть случайное событие, случайная величина, система случайных величин (случайный вектор) или случайная функция. Этот этап работы принято называть наблюдением. Данные, собранные и зафиксированные в ходе наблюдения, называются данными наблюдения.
В данной курсовой работе рассматриваются значения игровых показателей игроков НБА за сезон 2011/2012г.
1.1.2Упорядочение данных наблюдения
Выполнив
![]() независимых наблюдений над исследуемой
случайной величиной
независимых наблюдений над исследуемой
случайной величиной
![]() ,
получим
чисел:
,
получим
чисел:
![]() , (1)
, (1)
которые называются
наблюденными значениями, или реализациями,
этой случайной величины. Наблюденные
значения исследуемой случайной величины
в статистике принято рассматривать как
случайную выборку из бесконечной
генеральной совокупности реализаций
этой случайной величины, которые могли
бы быть получены при проведении всех
мыслимых наблюдений над этой случайной
величиной. При этом числа
![]() ,
,
![]() ,
образующие выборку, называют элементами
выборки, а число
этих элементов – объемом выборки.
Выборка является основным исходным
объектом любого статистического
исследования.
,
образующие выборку, называют элементами
выборки, а число
этих элементов – объемом выборки.
Выборка является основным исходным
объектом любого статистического
исследования.
Элементы случайной выборки (1), записанные в порядке их возрастания (неубывания),
![]() (2)
(2)
называются упорядоченной выборкой, или вариационным рядом.
1.1.3Способ равных интервалов
Группировка данных наблюдения способом равных частот осуществляется следующим образом:
Определяют число
 интервалов группировки и длину
интервалов группировки и длину
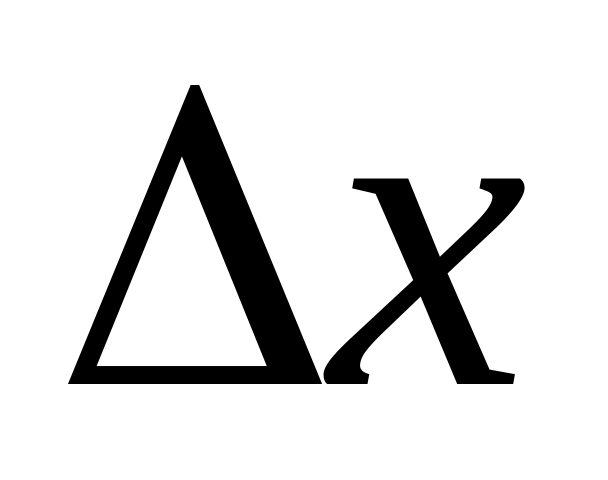 интервала группировки.
интервала группировки.Задаются «подходящим» значением
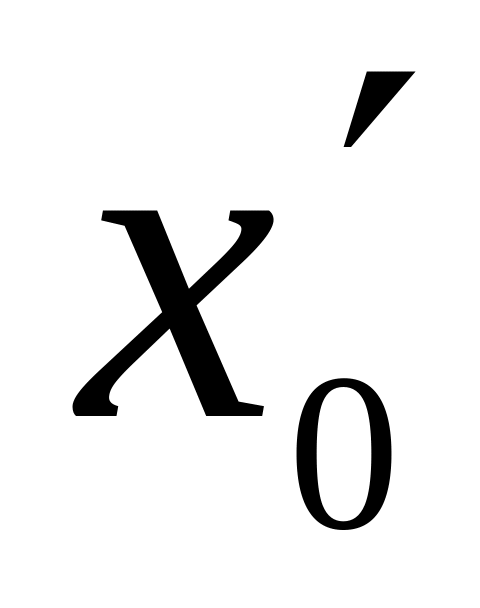 левой границы первого интервала
группировки.
левой границы первого интервала
группировки.С помощью формулы
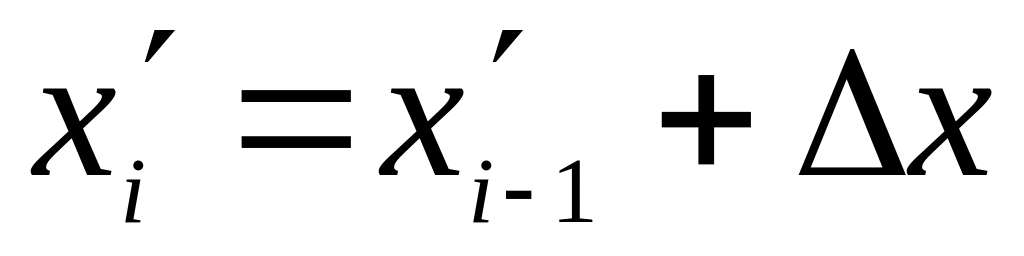 ,
,
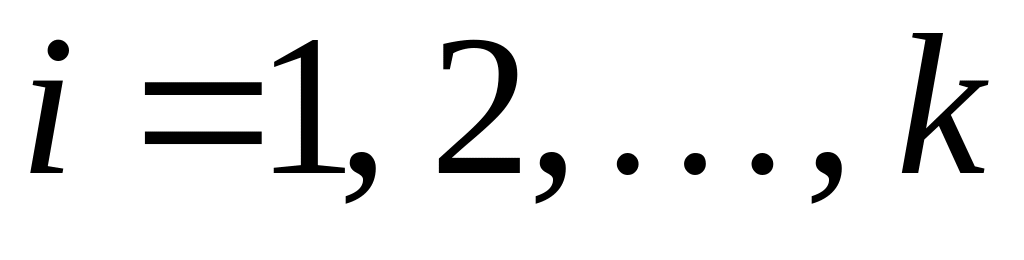 ,
вычисляют границы интервалов группировки.
,
вычисляют границы интервалов группировки.Подсчитывают групповые частоты
 попадания данных наблюдения в каждый
из интервалов группировки.
попадания данных наблюдения в каждый
из интервалов группировки.Составляют итоговую таблицу результатов группировки – таблицу частот.
Число интервалов группировки является целым числом и в Excel определяется по следующей формуле:
![]() . (3)
. (3)
1.1.4Способ равных частот
Группировка данных
наблюдения по равным интервалам имеет
существенный недостаток – при определении
числа
интервалов группировки и длинны
этих интервалов учитывается только
объем
выборки и ее размах
![]() и совершенно не учитываются
особенности распределения данных
наблюдения. От этого недостатка свободен
способ группировки, называемый способом
равных частот. Этот способ может быть
использован только при наличии
предварительного упорядоченных данных
наблюдения. Реализуется этот способ
следующим образом:
и совершенно не учитываются
особенности распределения данных
наблюдения. От этого недостатка свободен
способ группировки, называемый способом
равных частот. Этот способ может быть
использован только при наличии
предварительного упорядоченных данных
наблюдения. Реализуется этот способ
следующим образом:
Находят ориентировочное число
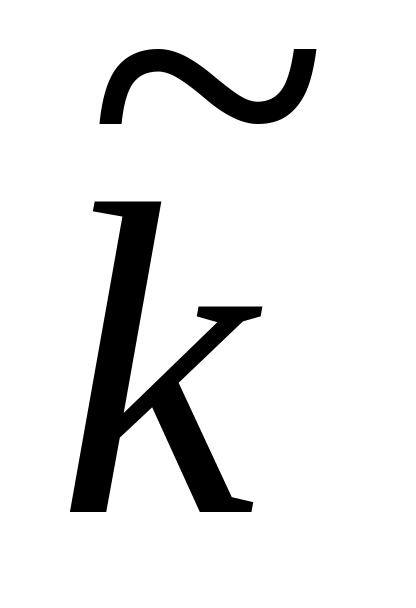 интервалов группировки по следующей
формуле:
интервалов группировки по следующей
формуле:
![]() . (4)
. (4)
Ориентировочное число данных наблюдения
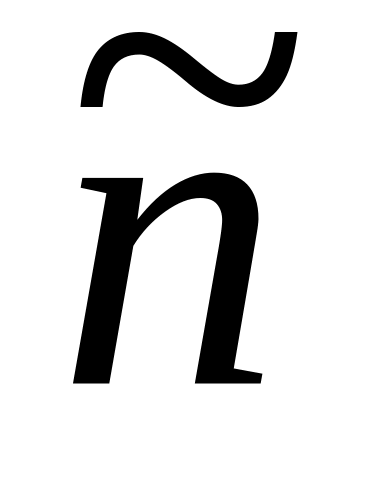 ,
приходящихся на один интервал группировки,
вычисляем по формуле:
,
приходящихся на один интервал группировки,
вычисляем по формуле:
![]() . (5)
. (5)
В качестве левой границы первого интервала группировки выбирают минимальный элемент
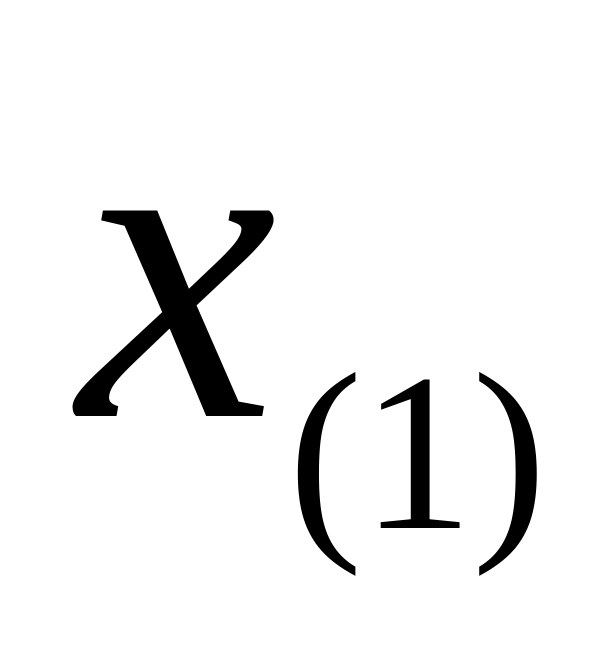 выборки.
выборки.В упорядоченной выборке
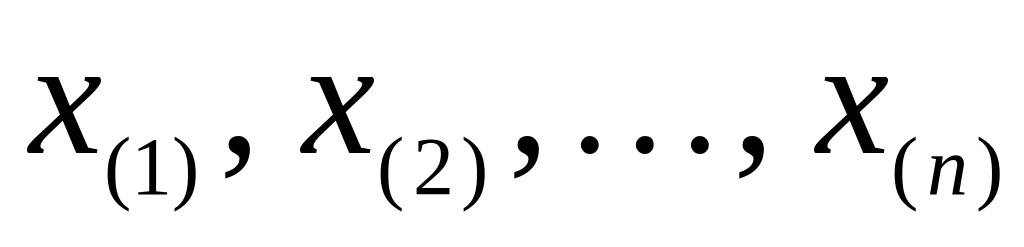 находят элемент
находят элемент
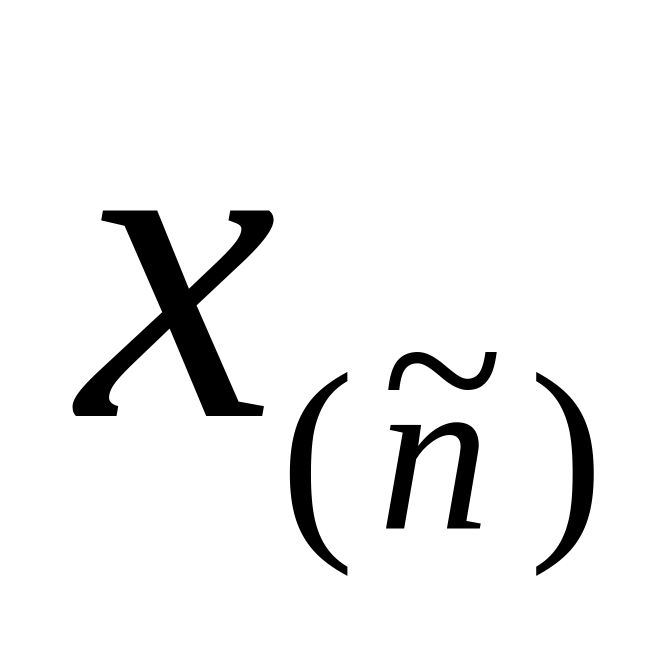 с номером
и сравнивают его с элементом
с номером
и сравнивают его с элементом
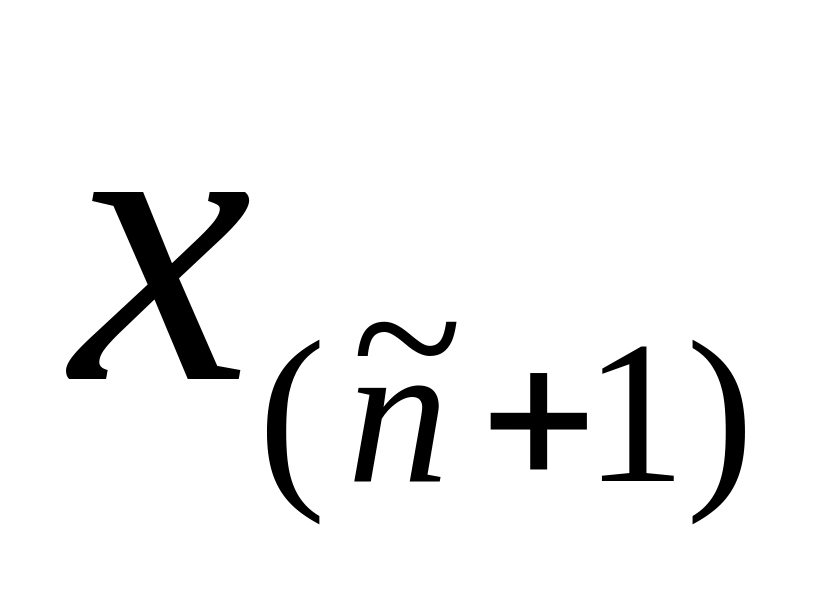 ,
имеющим номер
,
имеющим номер
 .
Если
.
Если
 ,
то полагают
,
то полагают
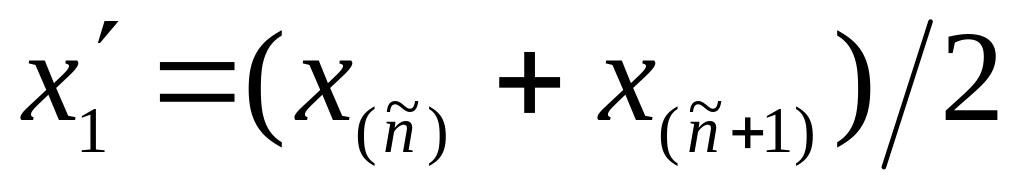 и
и
 ,
где
,
где
 – правая граница первого интервала
группировки и
– правая граница первого интервала
группировки и
 – групповая частота этого интервала.
Если же
– групповая частота этого интервала.
Если же
 ,
то сравнивают друг с другом элементы
упорядоченной выборки с номерами
и
,
то сравнивают друг с другом элементы
упорядоченной выборки с номерами
и
 .
При
.
При
 полагают
полагают
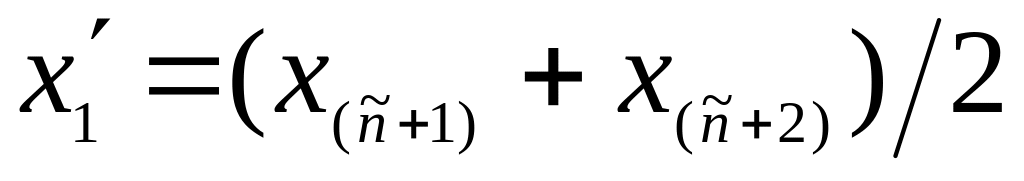 и
и
 .
В противном случае сравнивают элементы
.
В противном случае сравнивают элементы
 и
и
 .
И так продолжается до тех пор, пока не
будет найдена правая граница первого
интервала группировки.
.
И так продолжается до тех пор, пока не
будет найдена правая граница первого
интервала группировки.После определения отсчитывают наблюдений, превышающих , и сравнивают последнее из этих наблюдений со следующим за ним наблюдением. Если они не равны друг другу, то в качестве правой границы
 второго интервала группировки берут
их полусумму, а групповую частоту
второго интервала группировки берут
их полусумму, а групповую частоту
 второго интервала полагают равной
.
Если сравниваемые наблюдения совпадают
друг с другом, сравнивают следующую
пару наблюдений и т.д. В качестве правой
границы
второго интервала полагают равной
.
Если сравниваемые наблюдения совпадают
друг с другом, сравнивают следующую
пару наблюдений и т.д. В качестве правой
границы
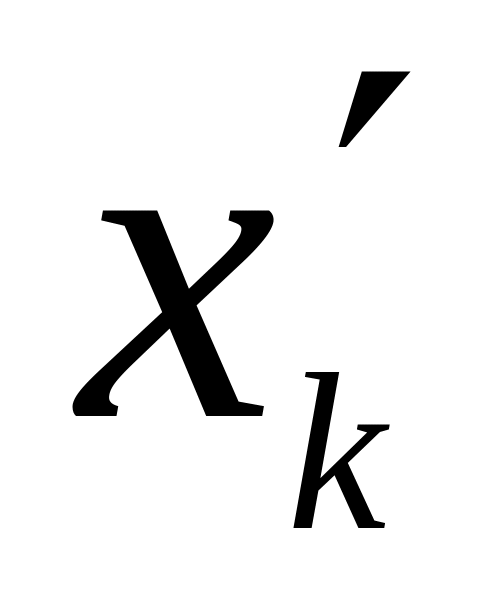 последнего интервала берут максимальный
элемент выборки.
последнего интервала берут максимальный
элемент выборки.
При реализации
способа равных частот интервалы
группировки имеют разную длину
![]() ,
а групповые частоты
,
а групповые частоты
![]() одинаковы или почти одинаковы. Исключение
может составлять только последний
интервал, групповая частота которого
может заметно отличаться от
.
одинаковы или почти одинаковы. Исключение
может составлять только последний
интервал, групповая частота которого
может заметно отличаться от
.
