1.3.6Проверка гипотезы о разности математических ожиданий двух кореллированных нормальных случайных величин с неизвестными дисперсиями (двухвыборочный t-критерий, сопряженные пары наблюдений)

При проверке гипотезы H₀: о том, что разность между математическими ожиданиями и двух кореллированных нормальных случайных величин и с неизвестными дисперсиями и равна заданному числу , используются не сами реализации , исследуемых случайных величин и , а их разности , , которые рассматриваются как реализации случайной величины . Критерий проверки данной гипотезы основан на статистике

, (24)

где и – выборочные оценки математического ожидания и дисперсии случайной величины ; – гипотетическое значение разности математических ожиданий и случайных величин и .

1.3.7Проверка гипотезы о значении дисперсии нормальной случайной величины

При проверке гипотезы H₀: о том, что дисперсия нормальной случайной величины равна заданному числу , используется статистика

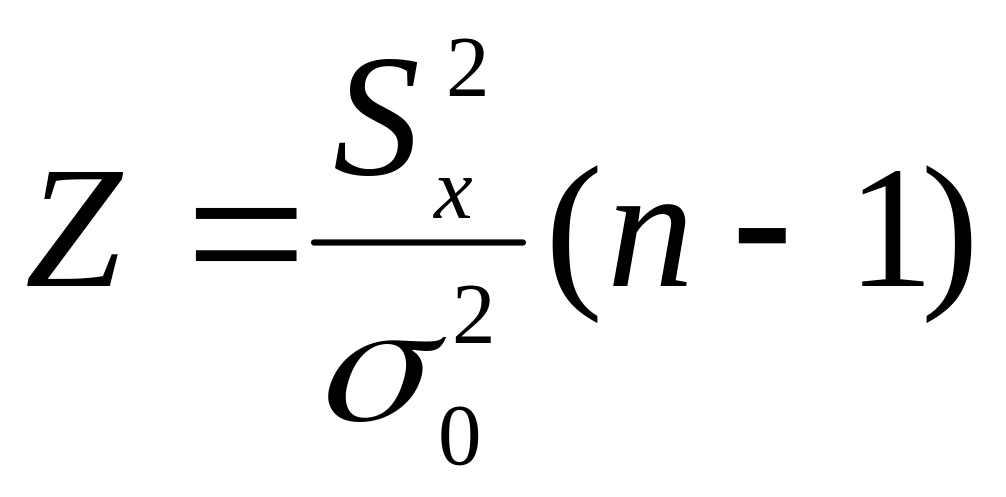, (25)

где – несмещенная оценка дисперсии нормальной случайной величины ; – объем выборки.

1.3.8Проверка гипотезы о равенстве дисперсий двух независимых нормальных случайных величин (F-критерий)

При проверке гипотезы H₀: о равенстве дисперсий и двух независимых нормальных случайных величин, и , используется статистика

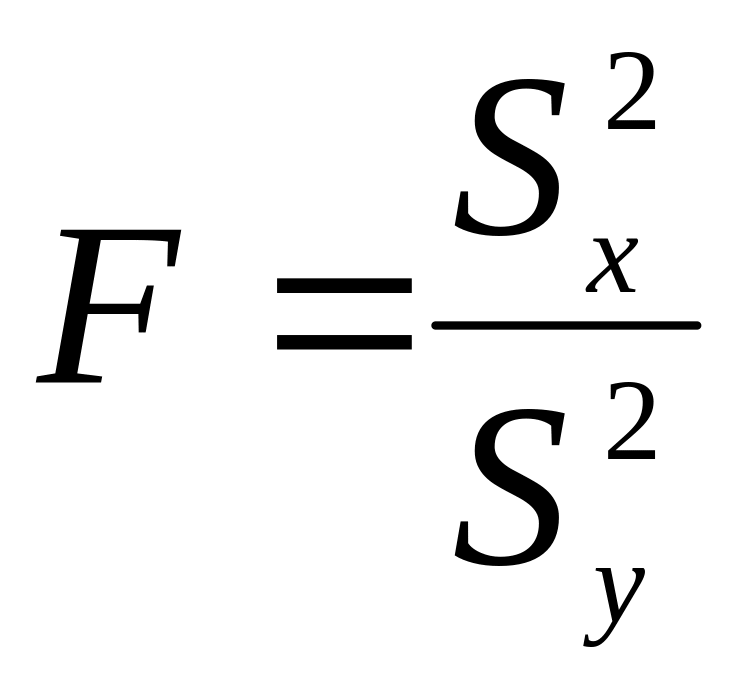, (26)

называемая дисперсионным отношением (здесь и – несмещенные оценки дисперсий и исследуемых нормальных случайных величин и , найденные по данным двух независимых выборок объемом и .

1.3.9Проверка гипотезы о равенстве дисперсий двух кореллированных нормальных случайных величин

При проверке гипотезы H₀: о равенстве дисперсий и двух кореллированных нормальных случайных величин, и , используется статистика

, (27)

где – выборочная оценка коэффициента корреляции нормальных случайных величин и .

1.3.10Проверка гипотезы о равенстве дисперсий нескольких независимых нормальных случайных величин (критерии Бартлета и Кокрена)

Наиболее распространенными критериями проверки гипотезы H₀: о равенстве дисперсий независимых нормальных случайных величин являются критерии Бартлета и Кокрена.

Критерий Бартлета.

В основе этого критерия лежит статистика

, (28)

где – число сравниваемых дисперсий (число выборок); – объем i-ой выборки; – суммарный объем всех выборок; – выборочная дисперсия -ой выборки; – выборочное среднее -ой выборки; – -ый элемент -ой выборки и

– (29)

взвешенное среднее выборочных дисперсий.

Критерий Кокрена

Этот критерий применяется в тех случаях, когда объемы всех выборок одинаковы (то есть когда ). В его основе лежит статистика

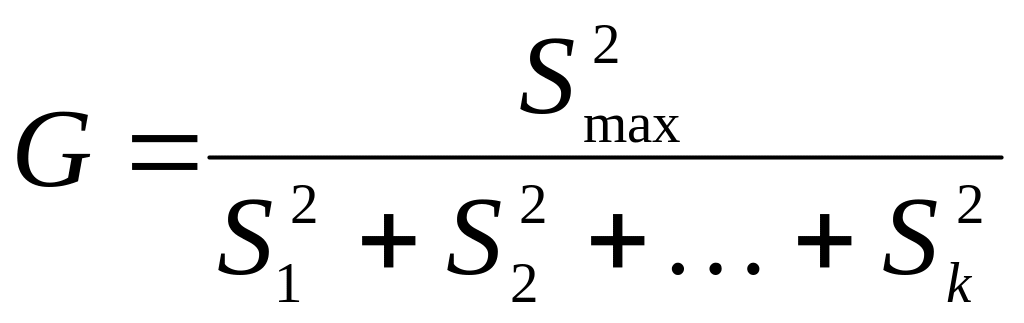, (30)

где – наибольшая из сравниваемых дисперсий.

1.4Проверка гипотезы о законе распределения случайной величины (критерии согласия)

1.4.1Критерий согласия хи-квадрат Пирсона

Проверка согласия с помощью этого критерия осуществляется по предварительно сгруппированным данным наблюдения. При этом в качестве меря расхождения между эмпирическим и гипотетическим распределениями используется статистика

, (31)

где – число интервалов группировки; – число реализаций исследуемой случайной величины , попавших в -ый интервал группировки (групповая частота -го интервала группировки); – число данных наблюдения (объем выборки); – вероятность попадания случайной величины в -ый интервал группировки при условии, что эта случайная величина подчиняется гипотетическому закону распределения (то есть при условии, что гипотеза H₀ верна).

Вероятности , , вычисляются по формулам

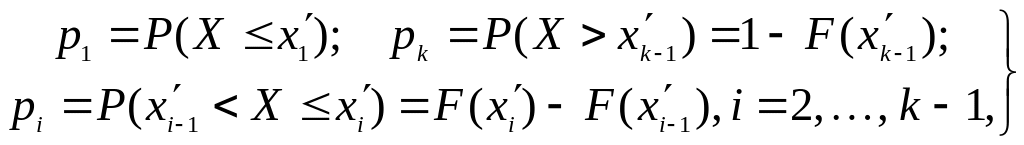(32)

где , – границы -го интервала группировки; – гипотетическая функция распределения.