1.4.2Критерий согласия Колмогорова
При проверке согласия по критерию Колмогорова в качестве меры расхождения между гипотетическими и истинным распределениями исследуемой случайной величины используется статистика
,
(33)
представляющая собой точную верхнюю границу абсолютной величины разности между гипотетической и эмпирической функциями распределения.
Расчетное значение
статистики
вычисляется с помощью формул
. (34)
1.4.3Критерий Крамера-Мизеса-Смирнова
В этом критерии
используется «весовая» функция
(то есть отклонения имеют одинаковый
«вес»). При этом статистика принимает
вид
. (35)
1.4.4Критерий Андерсона-Дарлинга
В этом критерии
используется «весовая» функция
.
При таком выборе
функции
«вес» отклонения увеличивается по мере
удаления
от центра распределения. При этом
статистика принимает вид
. (36)
1.4.5Критерии w Шапиро-Уилка
Эти критерии
зависят от распределения. Они используются
для проверки гипотез о том, что элементы
выборки
малого объема
являются реализациями нормальной
случайной величины
или случайной величины
,
имеющей показательное распределение.
А. При проверке гипотезы о том, что исследуемая случайная величины имеет нормальное распределение, используется статистика
, (37)
где
,
,
– постоянные, значения которых приведены
в таблице ПА.1 приложения А;
–
-ый
элемент упорядоченной выборки;
– несмещенная выборочная оценка
дисперсии
исследуемой
нормальной случайной величины
и
(то есть если
четное, то
;
если же
нечетное, то
,
при этом элемент
упорядоченной выборки в вычислениях
не используется).
Б. При проверке гипотезы о том, что исследуемая случайная величины имеет экспоненциальное (показательное) распределение, используется статистика
, (38)
где
и
– выборочные оценки математического
ожидания
и дисперсии
исследуемой случайной величины
.
В. При проверке
гипотезы о том, что исследуемая случайная
величины
имеет смещенное экспоненциальное
(показательное) распределение
,
с неизвестным смещением
,
используется статистика
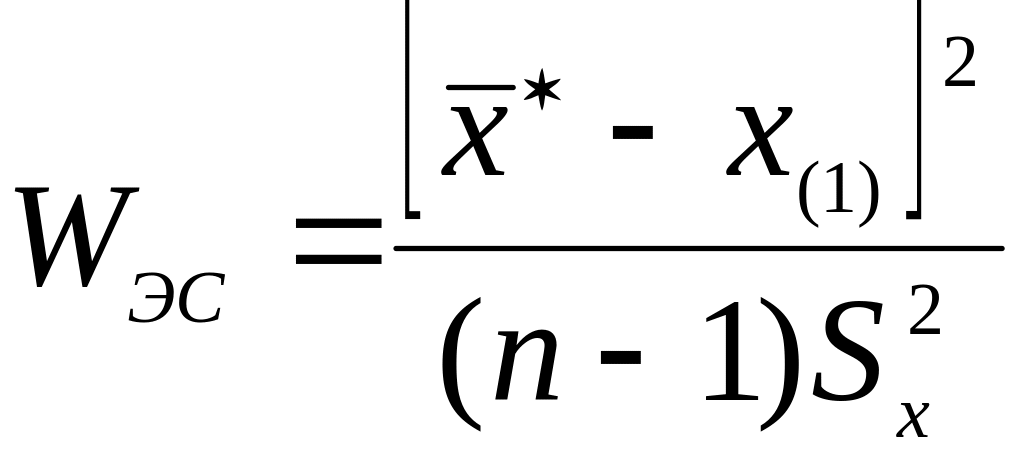, (39)
где
и
– выборочные оценки математического
ожидания
и дисперсии
исследуемой случайной величины
;
– минимальный элемент рассматриваемой
выборки.
2Практическая часть
2.1Первичная обработка статистических данных
2.1.1Исходные данные
В курсовой работе рассматриваются случайные величины – значения игровых показателей игроков НБА за сезон 2011/2012г.
Данные взяты из краткого статистического сборника «Россия в цифрах». Они предоставлены в форме числовых значений и являются непрерывными величинами. Исходные данные помещены в книге Excel на листе «Исходные данные» и показаны на рисунке 2.1.
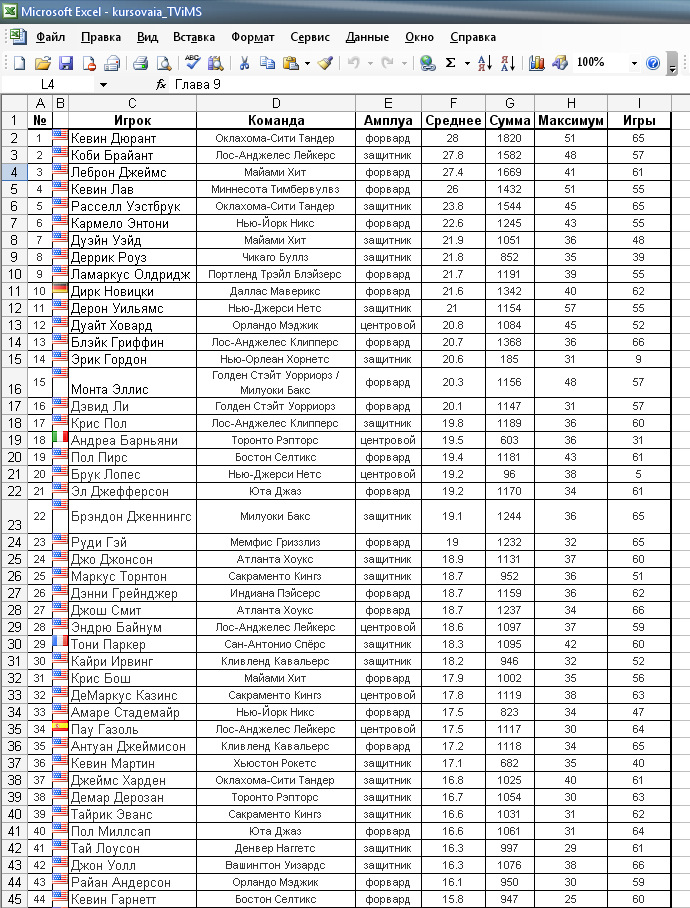
Рис. 2.1. Исходные данные
2.1.2Упорядочение данных наблюдения
Для выполнения данного этапа были взяты данные, представляющие собой значения игровых показателей игроков НБА за сезон 2011/2012г.
Результат представлен на листе Excel «Сортировка», а также на рисунке 2.2.
Рисунок 2.2. Упорядочение данных наблюдения
2.1.3Способ равных интервалов
Для выполнения данного этапа были взяты данные, представляющие собой значения игровых показателей игроков НБА за сезон 2011/2012г.
В Excel для реализации этого способа использовалась процедура Гистограмма. Результат представлен на листе Excel «Способ равных интервалов», а также на рисунке 2.3.
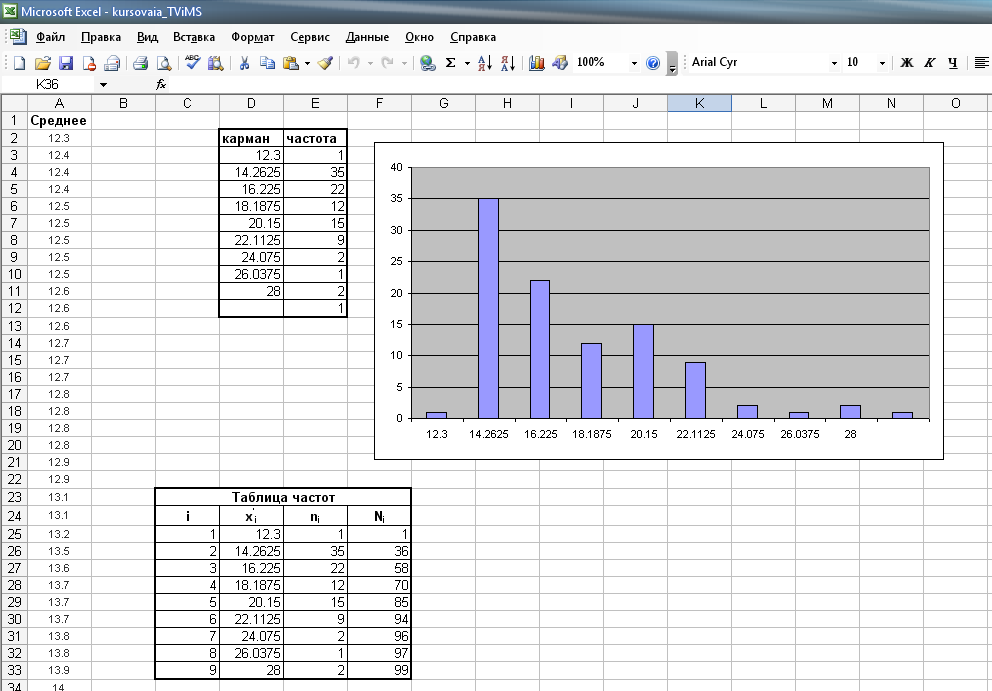
Рисунок 2.3. Способ равных интервалов
2.1.4Способ равных частот
Для выполнения данного этапа были взяты данные, представляющие собой значения игровых показателей игроков НБА за сезон 2011/2012г.
В Excel для реализации этого способа использовалась функция ЧАСТОТА.
Результат представлен на листе Excel «Способ равных частот», а также на рисунке 2.4.
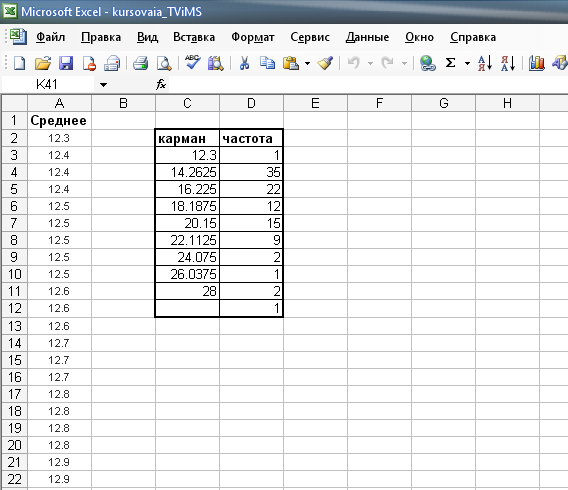
Рисунок 2.4. Способ равных частот
2.1.5Группировка данных наблюдения над дискретной случайной величиной
Для выполнения данного этапа были взяты данные, представляющие собой значения игровых показателей игроков НБА за сезон 2011/2012г оРоссию.
В Excel для реализации этого способа использовалась процедура Гистограмма.
Результат представлен на листе Excel «Групп. данных набл. над ДСВ», а также на рисунке 2.5.
Рисунок 2.5. Группировка данных наблюдения над дискретной случайной величиной