1.Векторна функція одного скалярного аргументу. Означення та приклади. Границя та неперервність векторної функції.

Векторною функцією (вектор – функцією ), заданою на множині , називається відображення, при якому кожному значенню відповідає вектор простору . .Постійний вектор називається границею векторної функції при , якщо для кожного існує таке, що для всіх , які задовольняють умові , виконується нерівність . Позначають: . Векторна функція називається неперервною в точці , якщо . Якщо векторна функція неперервна в усіх точках множини , то вона називається неперервною на цій множині.

2. Диференційованість векторної функції. Теорема про властивості диференційованих векторних функцій та наслідки з неї. Диференціювання складної векторної функції одного аргументу. Формула Тейлора.

Векторна функція називається диференційованою в точці , якщо при існує границя відношення .

(властивості диференційованих функцій). Якщо векторні функції , , і скалярна функція диференційовані в точці , то в цій точці диференційовані функції , , , , і мають місце рівності

1. ,

2. ,

3. ,

4. .

5.

(правило диференціювання складної функції). Нехай скалярна функція диференційована в точці , а векторна функція диференційована в точці . Тоді складна функція диференційована в точці , причому .

(формула Tейлора). Якщо векторна функція раз диференційована в точці й , то

,

де .

3. Поняття кривої. Способи завдання. Регулярність кривої. Особливі точки.

Параметризованой кривой наз. неп. отобр. γ :I→E_3, при котором ∀ tϵI соотв. т. MϵE₃ Кривой наз.годограф неп.векторной.фун-ии. Кривая задана при помощи вектор.функ-ии наз.гладкой кривой класса c^k , если имеет неп.производные до порядка k включительно. Задаются явно, неявно, параметрически. Кривая наз.регалярной, если для любой ее т.при переходящем выборе прямоугольной декартовой сист.координ. x,y,z она допускает в окр.этой точки задание уравнениями y=y(x), z=z(x). Особливі точки кривої - будь-яка точки кривої, що не є реґулярними.

4. Заміна параметра на кривій. Властивість допустимої заміни.

Замена параметра на кривой при помощи фан-ии τ=τ(t) наз.допустимой, если ∀t∈I ≠ -доп.замена параметра. Доп.замена параметра на кривой сохранаяет свойство регулярности.

5. Неявне завдання кривої. Теорема про неявно задану криву.

Кривая задана неявно, если её декартовы координаты удовлетворяют систему:

Теорема. Пусть 𝜔-мн-во т.простор.E₃ удовл.сист.(1). М₀(x₀,y₀,z₀)∈𝜔 и для неё выполняется условие ,тогда сущ.окресность т.M₀ такая что пересечение -регул.параметризованная кривая.

7. Дотична пряма та нормальна площина неявно заданої кривої.

Пусть F и Ф заданы неявным уравнением кривой, диференцируемые в неособой т.М₀(x₀,y₀,z₀) этой кривой, тогда явл.направляющим вектором касательной прямой в т.М_0.

Нормальной плоскостью кривой в т.М₀ наз.плоскость проход.через эту точку и перпендикулярная касательной прямой в т.М_0.

8.Стична площина кривої. Теорема про стичну площину.

Стичною площиною просторової кривої в даній її точці називається граничне положення, до якого прагне січна площина ( , за умови, що точки M1 й M2 прагнуть по кривій до точки .

Теорема. Усяка крива в будь-якій своїй бірегулярній точці має стичну площину, нормальним вектором якої є вектор [ ’( ), ’’( )].

9.Рухомий репер кривої. Дериваційні формули. Теорема про матрицю дериваційних формул ортонормованого реперу.

В диф.геометрії для вивчення кривих використовують рухомий репер. Нехай = , . Нехай визначає точку М цієї кривої. Розглянемо ще 3 вектора: . Фігура назив-ся рухомим репером в т. М

Деріваційними формулами рухомого репера назив-ся формули,які виражають похідні від векторів репера через базисні вектори цього ж реперу,тобто ’ = або

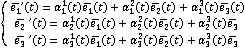
Теорема. Матриця дериваційних формул ортонормованого реперу кососиметрична.

10. Репер Френе кривої.Обчислення елементів реперу Френе.

Репером Френе кривої L у її точці M називають правий

декартів ортонормований репер {M,m1,m2.m3}, базисні вектори

якого визначають, відповідно, дотичну, головну нормаль і бінормаль

кривої L в точці M .

Щоб знайти координати векторів m1,m2.m3 репера Френе

кривої r =r(t) треба використати формули

.

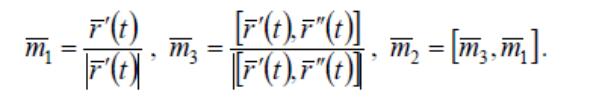
11.Довжина дуги кривої. Теорема про параметризацію кривої за допомогою довжини дуги.

Теорема. Будь-яка параметрична крива завжди може бути параметризована довжиною дуги і ця заміна являється допустимою.

длина дуги кривой в метрическом пространстве — числовая характеристика протяжённости этой кривой.

12. Натуральна параметризація кривої. Критерій натур-ї параметр-ї.

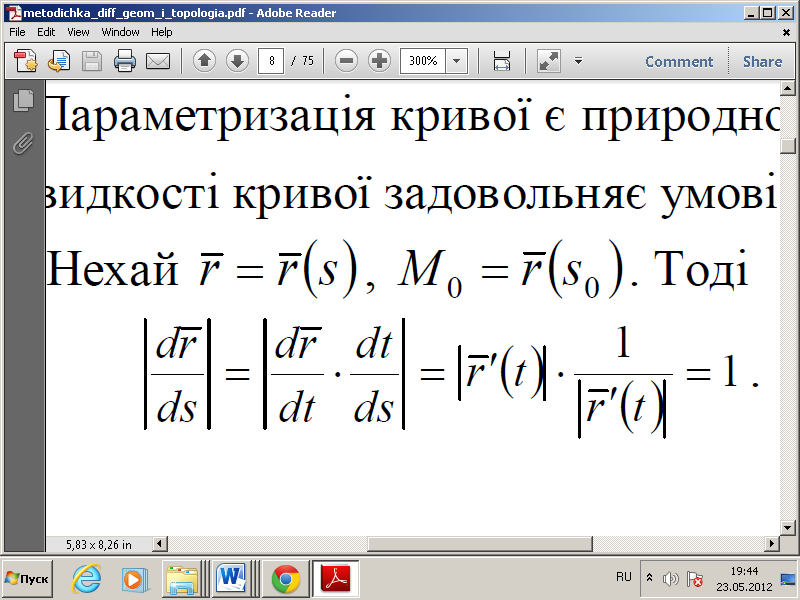
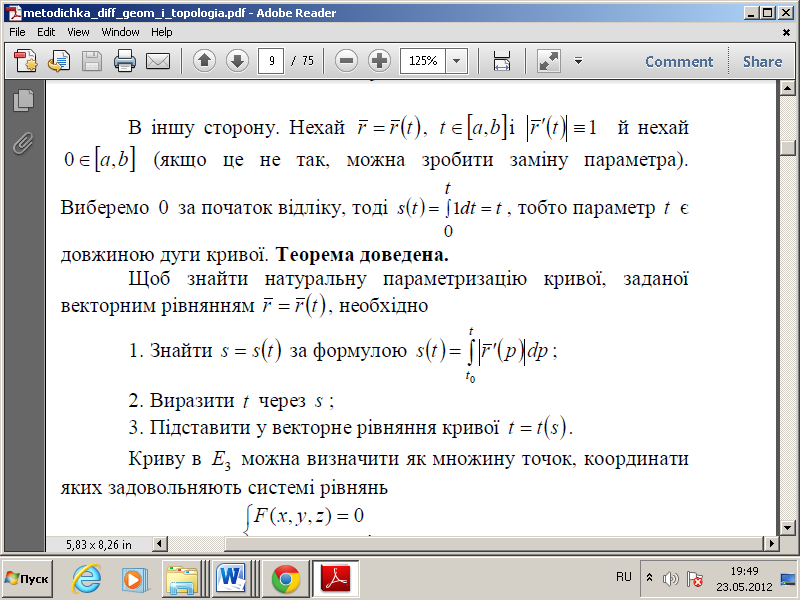
Параметризація кривої за допомогою довжини дуги, що

відлічується від деякої точки кривої, називається природною або

натуральною параметризацією.

Критерій натур-ї параметр-ї. Параметризація кривої є природною тоді й тільки

тоді, коли вектор швидкості кривої задовольняє умові º1.

Доведення:

13. Формули Френе. Означення та теорема.

Теорема. Деріваціонні формули репера Френе бірегулярної кривої параметризованою довжиною дуги мають вид:

Де -скалярні функції натурального

параметра s.

14. Означення кривини кривої. Теорема про кривину.

Нехай – крива класу , –фікс. Точкан на ній і М-достатньо близька до точка кривої, кривиною цієї кривої в т. назив. Границя відношення кута між дотичними в точках М і до довжини дуги при умові,що М . Позначається k( )=k( )

Теорема. Регулярна крива являється прямою або її частиною,тоді і лише тоді,коли в кожній її точці кривина дорівнює нулю.

15. Означення скруту кривої. Теорема про скрут.

Коефіцієнт у формулах Серре-Френе називається скрутом кривої . Очевидно, що абсолютний скрут є абсолютна велична вектора , тобто .

Теорема. Абсолютний скрут в точці М дорівнює кутовій швидкості обертання бінормалі кривої навколо точки М₀, тобто , де -кут повороту бінормалі, що відповідає приросту довжини дуги . Скрут буде додатнім (від’ємним), якщо при спостереженні з кінця вектора швидкості вектор бінормалі при русі точки по кривій обертається проти (по) годинникової стрілки.

16. Обчислення кривини кривої.

17. Обчислення скруту кривої.

18. Теорема про криві нульової кривини.

Теорема. Для того, щоб крива була прямою або її частиною (відрізком, променем), необхідно і достатньо щоб у кожній її точці кривина дорівнювала нулю.

19. Теорема про криві нульового скруту.

Теорема. Для того, щоб крива була плоскою, необхідно і достатньо, щоб у кожній її точці скрут дорівнював нулю.

20. Основна терема теорії кривих.

Теорема( основна теорема теорії кривих). Нехай на множині задані функції й класів і відповідно. Тоді існує єдина ( з точністю до положення в просторі) регулярна крива, для якої і є відповідно кривиною та скрутом в точці, яка відповідає значенню параметра .

21. Означення векторної функції двох скалярних аргументів. Диференціювання векторної функції.

Вектором-функцією двох аргументів заданою на , називається відображення, при якому кожній парі відповідає вектор

простору .

Невелика відмінність стосується диференціювання. Замість однієї похідної у вектора-функції двох аргументів є дві частині похідні, які будемо позначати або , або .

22. Поняття параметризованої поверхні. Регулярність поверхні. Приклади.

Нехай V - деяка область на площині R² з декартовими координатами u , v . Параметризованою поверхнею називається неперервне відображення з області V в простір E₃, при якому кожній парі (u,v) є V відповідає точка простору E. Змінні, u,v називаються параметрами поверхні. Образ області V називається образом або носієм поверхні.

Якщо виконується умова [r_u,r_v]≠0, то поверхня називається регулярною.

Нехай крива f: c(t)=(u(t),v(t)) , що задана в області V, регулярна. Тоді її образ на регулярній поверхні F : r = r (u,v), (u,v) є V також є регулярною кривою. Це так, тому що

вектор-функція R(t)=(u(t),v(t)), що задає образ регулярної кривої l на поверхні F, регулярна як складна функція двох регулярних функцій r (u,v), c(t).