Двойственные задачи

1.Составление двойственной задачи.Рассм.2 задачи ЛП:

Эти задачи обладают след.свойствами:

1) В одной задаче ищется max,а в другой min.

2) Коэф.при переменных в линейной формуле одной задачи явл. свободными членами системы ограничений др.задачи.

3)наоборот, своб. члены одной задачи-коэф.при переменных в линейной форме др.задачи.

4)в каждой задаче система ограничений задается в виде неравенста,причем они одного смысла(при нахождении max (≤) ,а при нахождении min (≥)

5)коэф.при переменных в системе ограничений опис.матрицами:

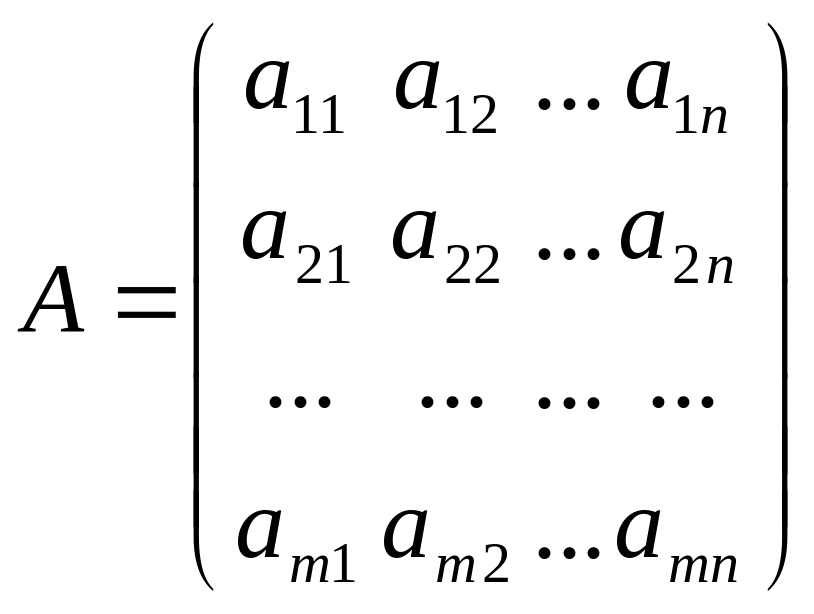
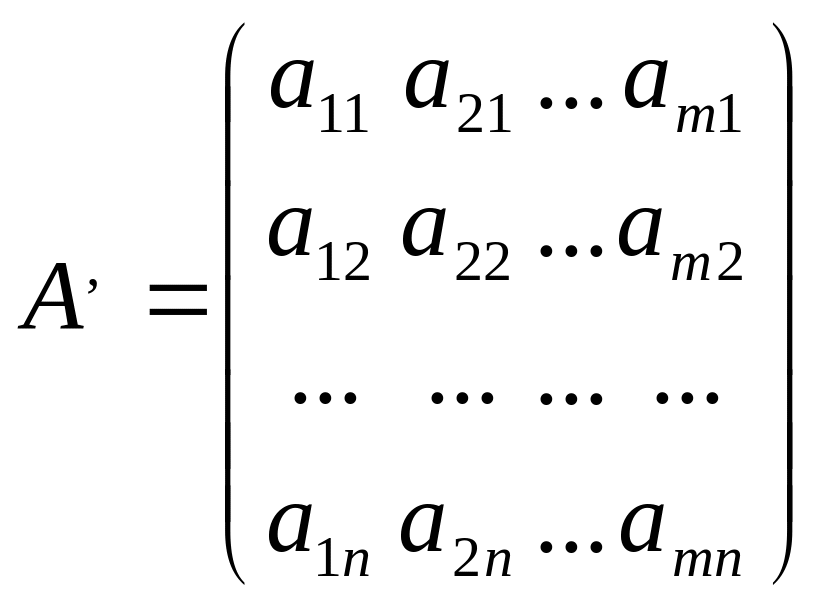
Кот.явл.транспонированными относительно друг другу.

Число неравенств в системе ограничений одной задачи совпадает с числом переменных 1ой задачи.

6) Условие неотриц.переменных сохраняется в обеих задачах.Две задачи ЛП,удовл.указанным выше условиям наз.симметричными взаимодвойственными задачами(двойственными). Таким образом,каждую задачу ЛП можно поставить в соотв.двойственную ей задачу.Первонач.задачу-в исходную(прямой).Прямая и двойств.ей задача,вместе взятые,образуют пару взаимнодвойств.задач.Причем любую из них можно рассм.как исходную,тогда др.окажется двоцйств.по отношению к исходной:

1.Приводят все неравенства системы ограничений исходной задачи к неравенствам одного смысла.Если в исходной задаче ищется max линейной формы,приводим к виду ≤,если min,то к виду ≥.Для этого неравенства,в кот.это требование не выполяется,умножим на (-1).

2.Выписываем матрицу А,коэф.при переменных исходной задачи,получ.после приобрет.в §1.И сост.матрицу А' трансопонир.относительно матрицы А.

3.Составляют систему огранич.двойств.задачи,взяв в качестве коэф.при переменных элемента матрицы А'.Свободные члены коэф.при переменных в линейной форме исходной задачи и запис.неравенство противопол.смысла по сравнению с неравенством,получ.в §1.

5.Указывают,что необх.найти при решении двойств.задачи (min линейной формы,если в исходной задаче ищется max и наоборот).

6.Записыв.условие неотрицательных переменных двойственной задачи.

Верхние и нижние цены игры

Среди всех чисел i i 1, 2, ,m выберем наибольшее . Назовм нижней ценой игры, или максимальным выигрышем максимином. Это гарантированный выигрыш игрока А при любой стратегии игрока В. Следовательно, . Стратегия, соответствующая максимину, называется максиминной стратегией. Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А выбирая стратегию Вj, он учитывает максимально возможный при этом выигрыш для А.

Обозначим . Среди всех чисел j выберем наименьшее и назовм верхней ценой игры или минимаксным выигрышем минимаксом. Это гарантированный проигрыш игрока В. Следовательно, . Стратегия, соответствующая минимаксу, называется минимаксной стратегией. Принцип, диктующий игрокам выбор наиболее осторожных минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника.

Термин «седловая точка» также используется для обозначения элемента матрицы, который является наименьшим элементом в своем ряду и наибольшим в своем столбце (или же наоборот, то есть наибольший в ряду и наименьший в столбце).

Например, матрица

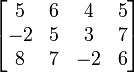
имеет одну седловую точку — «4» в первом ряду третьем столбце меньше, чем элементы в первом ряду матрицы («5», «6», «5»), и больше, чем элементы в третьем столбце («3», «-2»).

Матрица

содержит 4 седловых точки — «2» в первом и втором ряду, первом и четвёртом столбце. Данный пример показывает, что матрица может иметь любое количество седловых точек. Так, в матрице, состоящей из одного и того же числа, все элементы являются седловыми.

Матрица

не имеет седловой точки.

Вышеприведенное использование термина «седловая точка» имеет особое значение в теории игр. В играх с нулевой суммой равновесием Нэша явлется седловая точка.