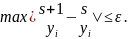- •Глава I. Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
- •Глава II. Численное моделирование теплового процесса приварки сварочной гильзы в полимерных армированных трубах
- •Введение Актуальность
- •Цель работы
- •Глава I Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
- •Однородные разностные схемы для уравнения теплопроводности
- •Сосредоточенный источник тепла
- •Цилиндрически-симметричные задачи теплопроводности
- •Квазилинейное уравнение теплопроводности
- •Метод суммарной аппроксимации
- •Методы решения задачи Стефана
- •Методы с выделением границы фазового перехода
- •Методы сквозного счета
- •Глава II Численное моделирование теплового процесса приварки сварочной гильзы в полимерных армированных трубах
- •Постановка задачи
- •Алгоритм задачи Стефана
- •Решение задачи теплопроводности по радиальной переменной
- •Решение задачи теплопроводности по осевой переменной
- •Заключение.
- •Список использованной литературы
Алгоритм задачи Стефана
Для решения задачи Стефана используем метод сглаживания коэффициентов с применением разностных схем сквозного счета [14], тем самым совершаем переход к обычной задаче теплопроводности.
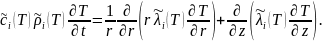 (1)
(1)
Здесь коэффициенты теплоемкости и теплопроводности имеют вид:
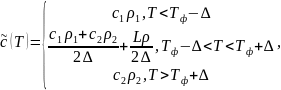 (2’)
(2’)
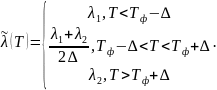 (3’)
(3’)
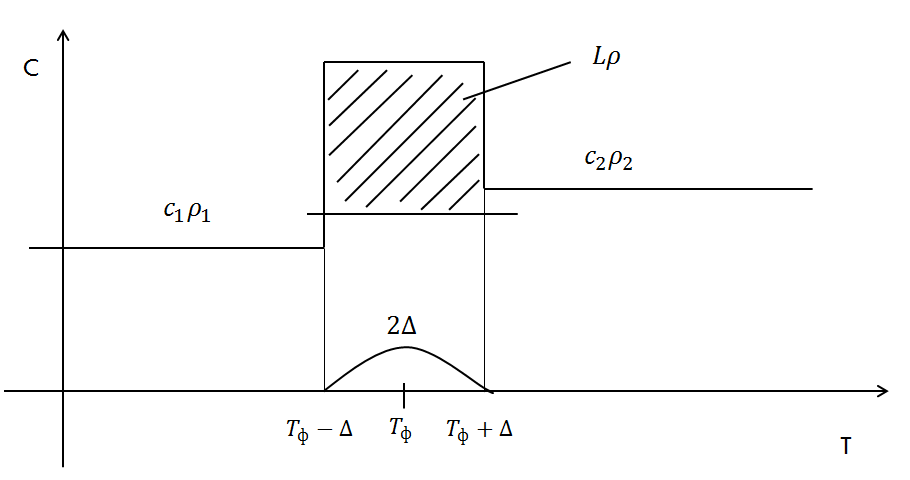
или
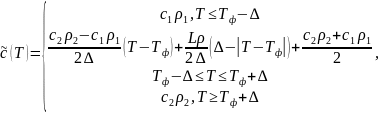 (2’’)
(2’’)
 (3’’)
(3’’)
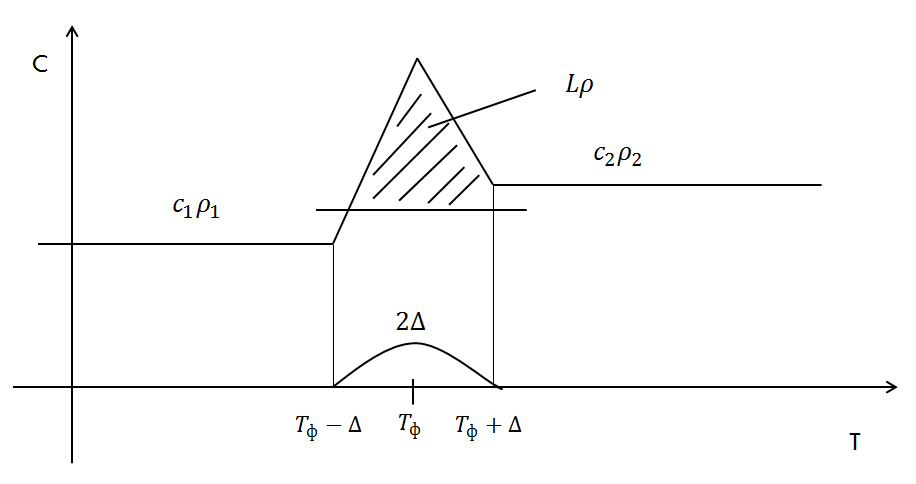
Далее задачу теплопроводности приведем к цепочке одномерных задач. Расщепление по r и z.
Решение задачи теплопроводности по радиальной переменной
Имеем цилиндрически-симметричную задачу теплопроводности:
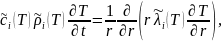 (1)
(1)
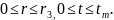
С начальными условиями:
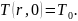 (2)
(2)
Краевыми условиями:
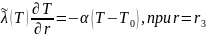 (3)
(3)
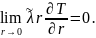 (4)
(4)
В месте расположения спирали задается условие сосредоточенного источника тепла:
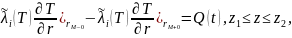 (5)
(5)
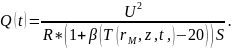 (6)
(6)
Обозначим L:
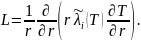 (7)
(7)
Введем сетку:
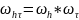
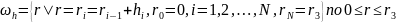 ,
,
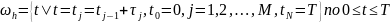 .
.
L аппроксимируем:
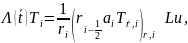 (8)
(8)
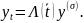 (9)
(9)
Задачу аппроксимируем методом баланса. Функции кусочно-непрерывны, поэтому
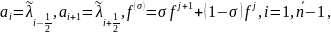
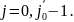
Возьмем σ=1.
Получаем неявную разностную схему,
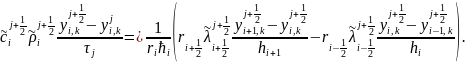 (10)
(10)
Разностная схема определена на шаблоне:
* * *
*
Коэффициенты являются нелинейными функциями, таким образом приходим к нелинейному уравнению теплопроводности и для нахождения ее решения используется метод итераций

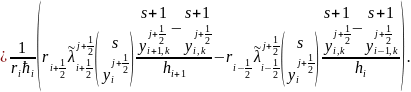 (11)
(11)
Относительно![]() разностная схема оказывается линейной.
разностная схема оказывается линейной.
Задача
в точке
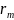 имеет в наличии сосредоточенный источник
тепла и удовлетворяет условию сопряжения.
Уравнение примет вид
имеет в наличии сосредоточенный источник
тепла и удовлетворяет условию сопряжения.
Уравнение примет вид
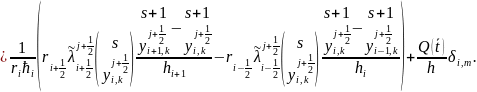 (12)
(12)
Граничное условие (3) аппроксимируем методом баланса, σ=1:
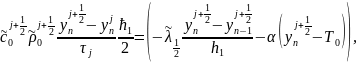 (13)
(13)
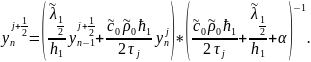 (14)
(14)
Аппроксимируем краевое условие (4) приr=0, σ=1:
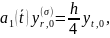
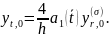 (15)
(15)
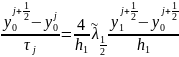 ,
,
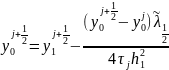 .
.
Получим систему линейных алгебраических уравнений с трехдиагональной матрицей [15-18]. Такая система решается методом прогонки:
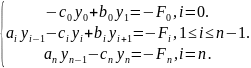
Найдем коэффициенты системы:
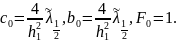
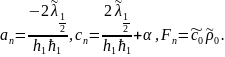
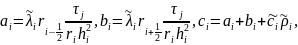
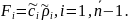
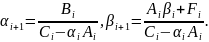
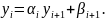
Решение задачи теплопроводности по осевой переменной
Имеем обычную задачу теплопроводности в декартовых координатах:
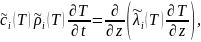 (1)
(1)
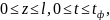
С начальными условиями:
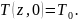 (2)
(2)
Краевыми условиями:
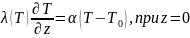 (3)
(3)
 (4)
(4)
Введем сетку:
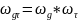
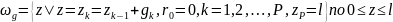 ,
,
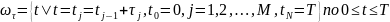 .
.
Задачу аппроксимируем методом баланса. Функции кусочно-непрерывны, поэтому
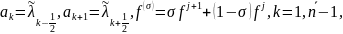
Возьмем σ=1.
Получаем неявную разностную схему. Коэффициенты являются нелинейными функциями, таким образом приходим к нелинейному уравнению теплопроводности и для нахождения ее решения используется метод итераций:
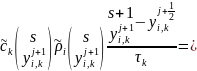
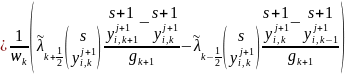 .
(4)
.
(4)
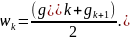
Граничное условие (3) аппроксимируем методом баланса
Возьмем σ=1
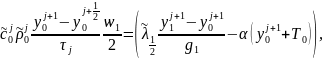
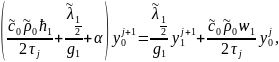
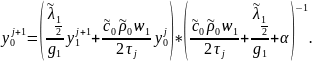 (5)
(5)
Условие (4) первого рода аппроксимируется точно:
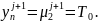
Получаем систему линейных алгебраических уравнений с трехдиагональной матрицей. Решаем методом прогонки:
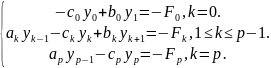
Найдем коэффициенты системы:
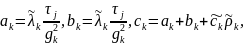
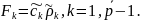
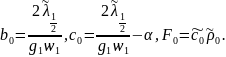
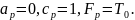
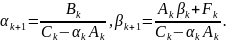
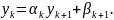
В
качестве начального приближения берется
функция температуры с предыдущего шага
по времени: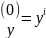 .
Прекращаем итерации по условию:
.
Прекращаем итерации по условию: