Методы сквозного счета
Двухфазная задача Стефана
Классическая задача Стефана допускает обобщенную формулировку в виде одного нелинейного уравнения теплопроводности, при которой реализуются необходимые условия на границе фазового перехода. Это дает возможность строить вычислительные алгоритмы приближенного решения задач с фазовыми превращениями без явного выделения свободной границы. О таких методах мы говорим как о методах сквозного счета.
Рассматривается
модельная двухфазная задача Стефана в
прямоугольнике
.
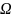Свободная граница
разбивает
,
на две подобласти
и
.
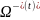В обоих подобластях выполняется уравнение
теплопроводности. Как обычно, будем
считать, что теплофизические параметры
твердой и жидкой фаз постоянны, для
обозначения принадлежности к той или
иной области будем использовать индекс
«+» или «-».
Запишем в каждой подобласти уравнение теплопроводности
В начальный момент задается некоторое распределение температуры:
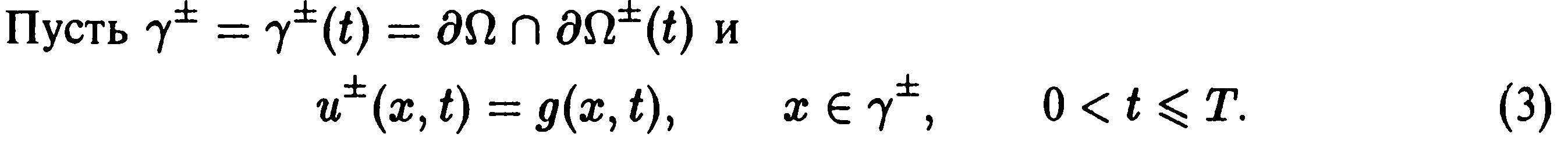
Температуру фазового перехода принимаем равной нулю и поэтому свободная граница определяется следующим образом:
На ней выполнены два условия сопряжения, отражающие непрерывность температуры и закон сохранения тепла:
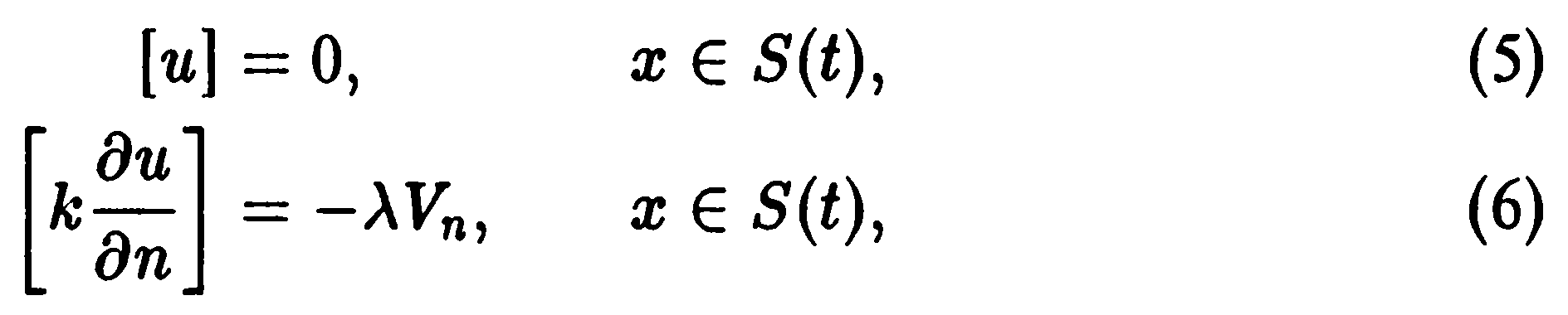
где
λ — энтальпия фазового перехода, a
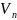— скорость движения свободной границы
по нормали к
.
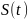Рассматриваемая
двухфазная задача Стефана (1)-(6) может
быть записана в виде одного общего
уравнения теплопроводности во всей
области
.
Пусть
— дельта-функция, тогда вместо уравнений
(1) и условий сопряжения (4)-(6) можно
рассматривать одно уравнение
теплопроводности
Здесь коэффициенты теплоемкости и теплопроводности разрывны и имеют вид
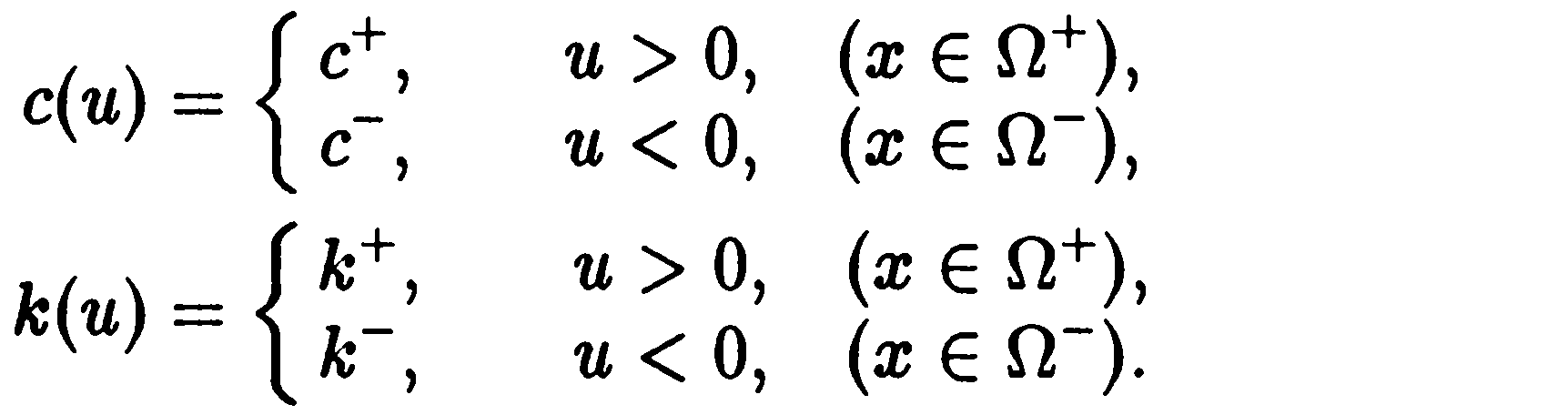
В соответствии с (2) и (3) уравнение (7) дополняется условиями
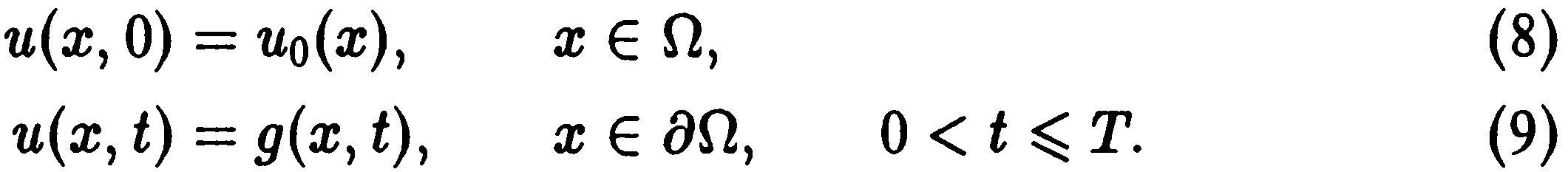
Особенность задачи Стефана проявляется в наличии слагаемого с δ функцией в левой части уравнения (7). Выделение или поглощение тепла при фазовом переходе соответствует наличию сосредоточенной теплоемкости на границе фазового перехода. Сама краевая задача (7)-(9) не очень сильно отличается от рассмотренных выше квазилинейных задач теплопроводности. Это позволяет нам перейти к построению соответствующих разностных схем.
Разностная схема со сглаженными коэффициентами
Простейший подход к приближенному решению задачи Стефана в формулировке (7)-(9) состоит в том, что коэффициенты уравнения (7) сглаживаются, т. е. совершается переход к обычной задаче теплопроводности.
В
уравнении (7) теплоемкость
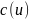и слагаемое
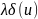входят одинаковым образом. Заменим
δ-функцию
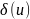некоторой
функцией
,
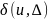которая отлична от нуля только внутри
интервала сглаживания
,
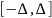и введем эффективную сглаженную
теплоемкость
При
необходимости проводится сглаживание
и коэффициента теплопроводности
(
заменяется
на
)
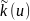и вместо уравнения (7) ищется решение
уравнения со сглаженными коэффициентами
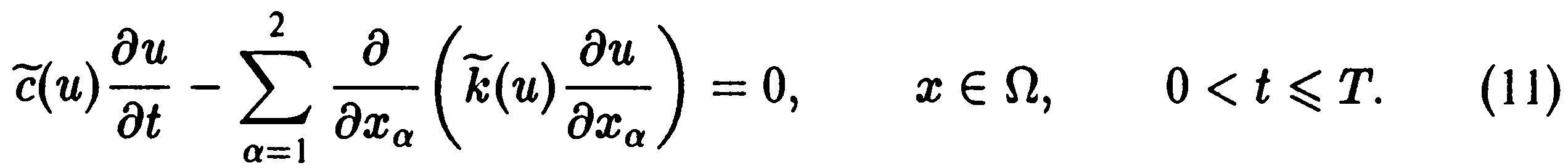
В вычислительной практике получили распространение различные аппроксимационные формулы для , которые строятся из условия сохранения баланса тепла на интервале . Простейшая их них связана с заданием
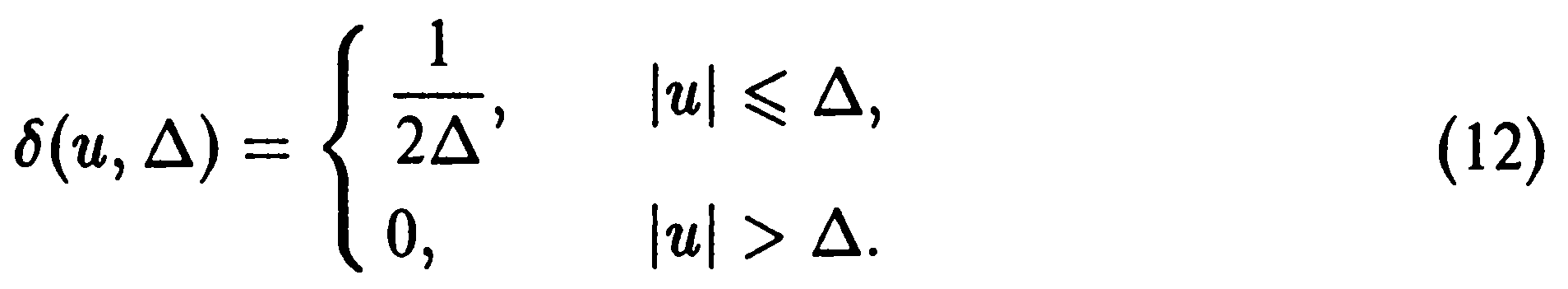
В качестве второго примера может отметить параболическую аппроксимацию, когда
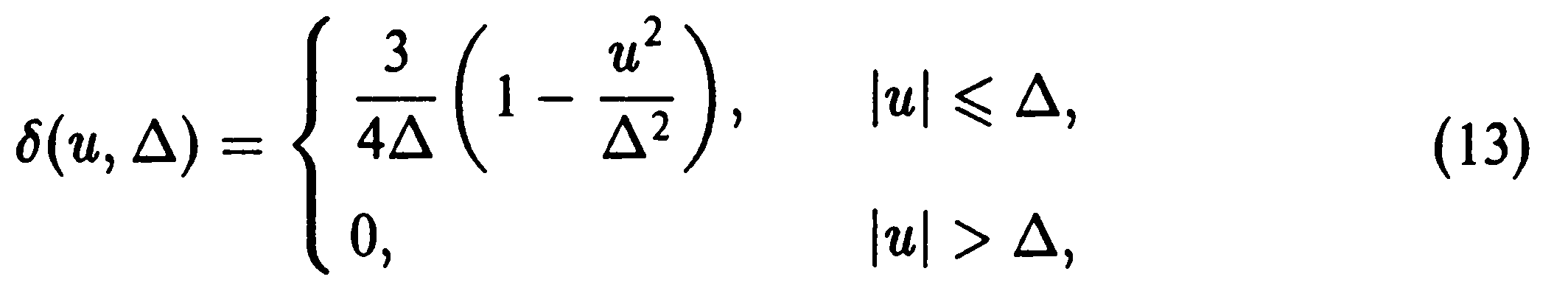
для которой условие
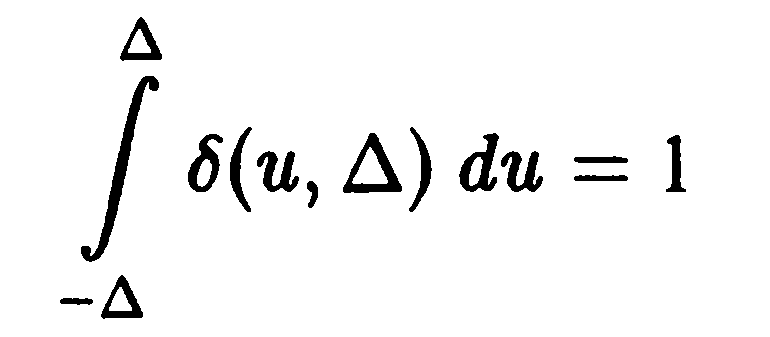
также,
очевидно, выполнено. Как показывают
численные эксперименты, точность
разностного решения слабо зависит от
выбора той или иной аппроксимационной
формулы для δ -функции, в частности, от
выбора (12) либо (13). Более существенное
влияние оказывает величина параметра
сглаживания
,
который естественно зависит от
используемой сетки и определяется, чаще
всего, эмпирически в результате
методических расчетов.
В методах сквозного счета разностную схему строят на основе использования уравнения (11), считая коэффициенты этого уравнения достаточно гладкими. Сама граница фазового перехода не выделяется, не участвует в построении разностной схемы. При необходимости свободная граница идентифицируется как нулевая изотерма после того, как решение найдено.
Для решения задачи (8), (9), (11) применяются рассмотренные ранее разностные методы. Применим, например, чисто неявную разностную схему
здесь
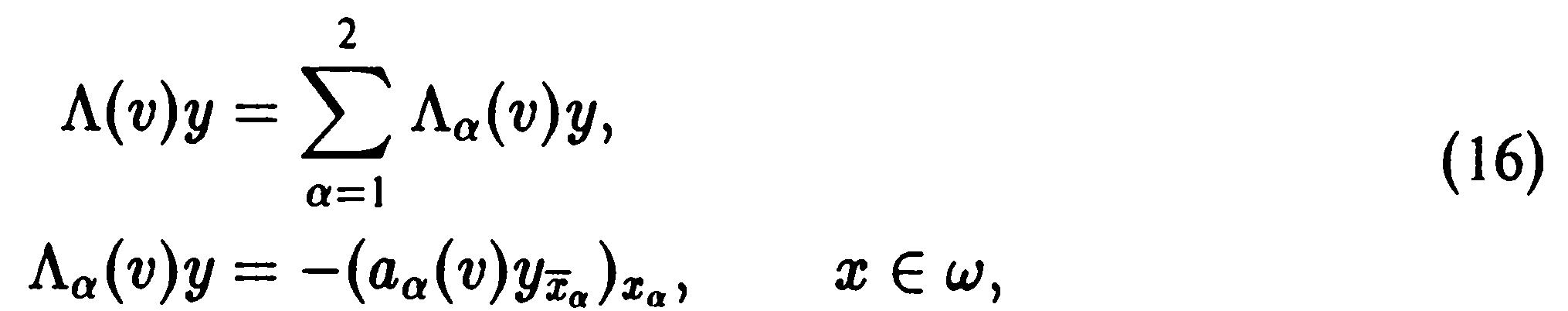
Граничные и начальные условия (8), (9) дают
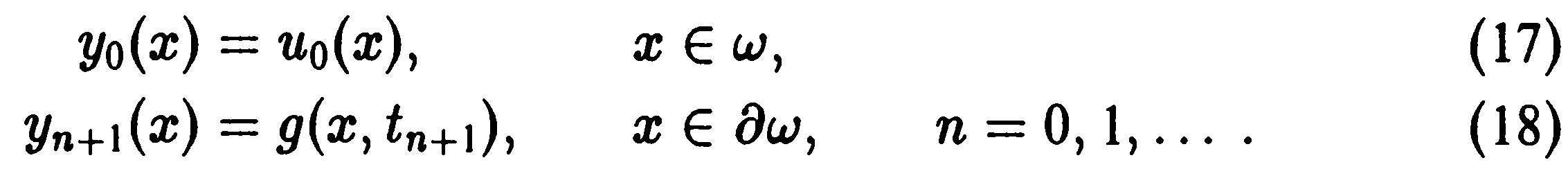
Для определенности положим
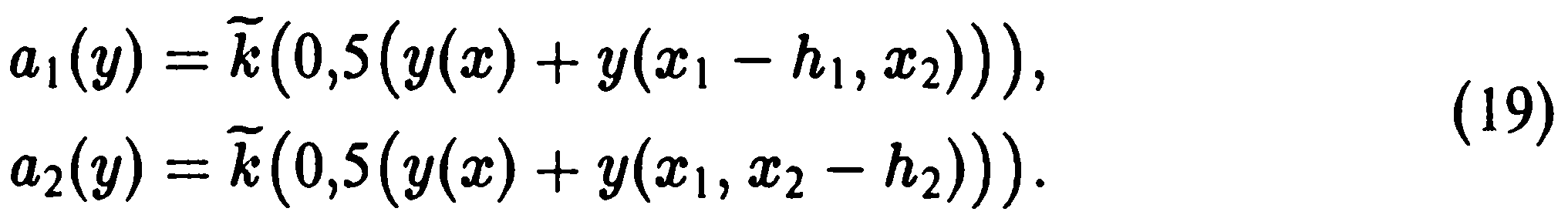
Реализация нелинейной разностной схемы (14)—(19) осуществляется на основе итерационных методов. Простейший из них связан с итерационным уточнением коэффициентов. Новое приближение находится из решения линейной разностной задачи
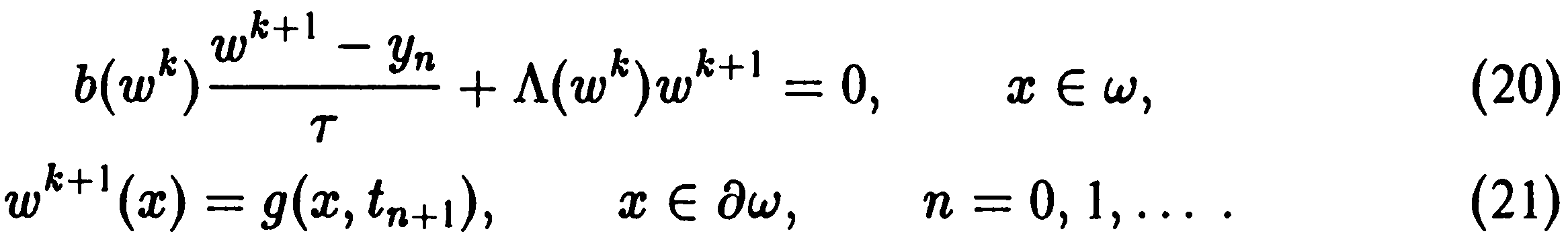
Как правило, достаточно нескольких итераций (20), (21), чтобы обеспечить хорошую точность. Вместо итерационного процесса (20), (21) можно использовать метод Ньютона, который приводит к несамосопряженной сеточной эллиптической задаче для нового приближения.