- •Глава I. Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
- •Глава II. Численное моделирование теплового процесса приварки сварочной гильзы в полимерных армированных трубах
- •Введение Актуальность
- •Цель работы
- •Глава I Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
- •Однородные разностные схемы для уравнения теплопроводности
- •Сосредоточенный источник тепла
- •Цилиндрически-симметричные задачи теплопроводности
- •Квазилинейное уравнение теплопроводности
- •Метод суммарной аппроксимации
- •Методы решения задачи Стефана
- •Методы с выделением границы фазового перехода
- •Методы сквозного счета
- •Глава II Численное моделирование теплового процесса приварки сварочной гильзы в полимерных армированных трубах
- •Постановка задачи
- •Алгоритм задачи Стефана
- •Решение задачи теплопроводности по радиальной переменной
- •Решение задачи теплопроводности по осевой переменной
- •Заключение.
- •Список использованной литературы
Цель работы
Целью работы является разработка алгоритма численного решения задачи определения нестационарного температурного поля при приварке сварочной гильзы в полимерных армированных трубах.
Для достижения цели поставлены следующие задачи:
Поставить задачу Стефана для определения нестационарного температурного поля при приварке сварочной гильзы в полимерных армированных трубах с учетом теплоты фазового перехода при оплавлении и кристаллизации полиэтилена;
Изучить методы численного решения фронтовой задачи Стефана и выбрать наиболее эффективный метод для решения поставленной задачи;
Построить алгоритм численного решения задачи.
Глава I Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
Разностная схема — это конечная система алгебраических уравнений, поставленная в соответствие какой-либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия (например: краевые условия и/или начальное распределение). Таким образом, разностные схемы применяются для сведения дифференциальной задачи, имеющей континуальный характер, к конечной системе уравнений, численное решение которых принципиально возможно на вычислительных машинах. Алгебраические уравнения, поставленные, в соответствие дифференциальному уравнению получаются применением разностного метода, что отличает теорию разностных схем от других численных методов решения дифференциальных задач.
Аппроксимация . Научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов.
Устойчивость. Условия аппроксимации не достаточно для того, чтобы результат разностной схемы приближался к точному ответу при h→0. В случае схем, коэффициенты которых не зависят от решения дифференциального уравнения, нужно выполнение условия устойчивости. Такие схемы можно представить как некоторый линейный оператор, который преобразует значения функции в момент t в значения функции в момент t+τ. Условие устойчивости требует, чтобы собственные числа (вообще говоря комплексные) этого оператора не превосходили по модулю 1+ch, где с — некоторая константа, при h→0. Если это условие не выполнено, то погрешности схемы быстро возрастают и результат тем хуже, чем меньше шаг. Если выполнены как условие аппроксимации, так и условие устойчивости, то результат разностной схемы сходится к решению дифференциального уравнения.
Однородные разностные схемы для уравнения теплопроводности
![]()
В связи с широким применением вычислительных машин становится ясным, что нецелесообразно использовать разностные схемы и составлять программы, предназначенные лишь для решения отдельных задач частного вида. Необходимо иметь разностные схемы, пригодные для решения классов задач, определяемых заданием типа дифференциального уравнения, класса краевых и начальных условий, а также функционального пространства, которому принадлежат коэффициенты дифференциального уравнения. Такие универсальные разностные схемы должны, естественно, удовлетворять требованиям сходимости и устойчивости на любой последовательности сеток и для любой исходной задачи из рассматриваемого класса задач. Требование единообразия вычислительного алгоритма для решения класса задач приводит к понятию однородных разностных схем. Под однородной разностной схемой понимается разностная схема, вид которой не зависит ни от выбора конкретной задачи из данного класса, ни от выбора разностной сетки. Во всех узлах сетки для любой задачи из данного класса разностные уравнения имеют один и тот же вид. Коэффициенты однородной разностной схемы определяются как функционалы коэффициентов дифференциального уравнения[13][23].
Большой интерес, например, представляет отыскание однородных схем «сквозного» или «непрерывного» счета, пригодных для решения уравнения теплопроводности (диффузии) с разрывным коэффициентом теплопроводности (диффузии) по одним и тем же формулам (программам) без явного выделения точек или линий разрыва коэффициентов. Это значит, что схема в окрестности разрывов не меняется и вычисления во всех узлах ведутся по одним и тем же формулам, независимо от того, разрывен или непрерывен коэффициент теплопроводности.
Использование однородных схем сквозного счета особенно важно в тех случаях, когда коэффициент теплопроводности вычисляется в результате приближенного решения других уравнений, что, например, имеет место при решении уравнений газодинамики в теплопроводном газе, когда коэффициент теплопроводности зависит от плотности и терпит разрывы на ударных волнах.
Будем
рассматривать разностные операторы
над функциями одного переменного
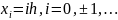 Разностный
оператор вначале определяется на
целочисленном шаблоне , т. е. на множестве
Разностный
оператор вначале определяется на
целочисленном шаблоне , т. е. на множестве
![]()
где
 —целые
числа, после чего совершается переход
к реальной сетке
—целые
числа, после чего совершается переход
к реальной сетке
![]()
С
шагом h.
Пусть
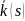 – вектор-функция заданная на отрезке
– вектор-функция заданная на отрезке

Рассмотрим первую краевую задачу для стационарного уравнения теплопроводности

Эта задача имеет решение, если k(x), q(x), f (x) кусочно-непрерывные функцииЕсли k(x) имеет разрыв первого рода в точке x=ξ, так что
[k] = k (ξ+0) - k (ξ-0)≠0 то при x = ξ ставятся условия сопряжения
![]()
При х = 0 и х = 1 могут быть заданы краевые условия
![]()
Если, например β> 0, то это условие третьего рода, при β=0—условие второго рода. Возможны различные комбинации условий первого, второго и третьего рода (например, при х =0—условие третьего рода, при х=1— условие первого рода и т. д.).
На отрезке [0, 1] введем равномерную сетку
![]()
с шагом h = 1/N; обозначим
![]()
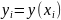 – сеточная функция
– сеточная функция
При
написании схемы, аппроксимирующей
уравнение (1) возьмем трехточечный шаблон
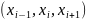 .
Любое трехточечное разностное уравнение
на этом шаблоне можно записать в виде
.
Любое трехточечное разностное уравнение
на этом шаблоне можно записать в виде![]()
где
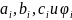 зависят от шага h,
или в виде
зависят от шага h,
или в виде
![]()
где
![]() Коэффициенты
Коэффициенты
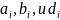 и правая часть
и правая часть
 пока
не определены.
пока
не определены.
Консервативные схемы
При написании разностных схем следует добиваться, чтобы эти схемы выражали на сетке соответствующий закон сохранения. Такие схемы мы будем называть консервативными.
Различные физические процессы (теплопроводности или диффузии, колебаний, газодинамики и т. д.) характеризуются некоторыми интегральными законами сохранения (тепла, массы, количества движения, энергии и т. д.).
При выводе дифференциальных уравнений математической физики обычно исходят из некоторого интегрального соотношения (уравнения баланса), выражающего закон сохранения для малого объема. Дифференциальное уравнение получается из уравнения баланса при стягивании объема к нулю в предположении существования непрерывных производных, входящих в уравнение.
Метод конечных разностей физически означает переход от непрерывной среды к некоторой ее дискретной модели. При таком переходе естественно требовать, чтобы основные свойства физического процесса сохранялись. Такими свойствами, прежде всего, являются законы сохранения. Разностные схемы, выражающие на сетке законы сохранения, называют консервативными (или дивергентными). Законы сохранения для всей сеточной области («интегральные законы сохранения») для консервативных схем должны быть алгебраическим следствием разностных уравнений.
Для получения консервативных разностных схем естественно исходить из уравнений баланса, записанных для элементарных объемов (ячеек) сеточной области. Входящие в эти уравнения баланса интегралы и производные следует заменить приближенными разностными выражениями. В результате получаем однородную разностную схему. Такой метод получения консервативных однородных разностных схем будем называть интегро-интерполяционным методом (методом баланса).
Проиллюстрируем этот интегро-интерполяциоиный метод на примере уравнения
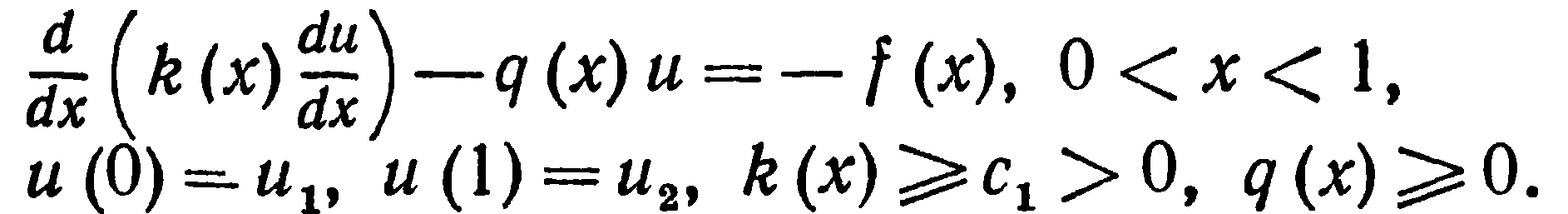
описывающего
стационарное распределение температуры
в однородном стержне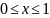 .
Напишем уравнение баланса тепла на
отрезке
.
Напишем уравнение баланса тепла на
отрезке

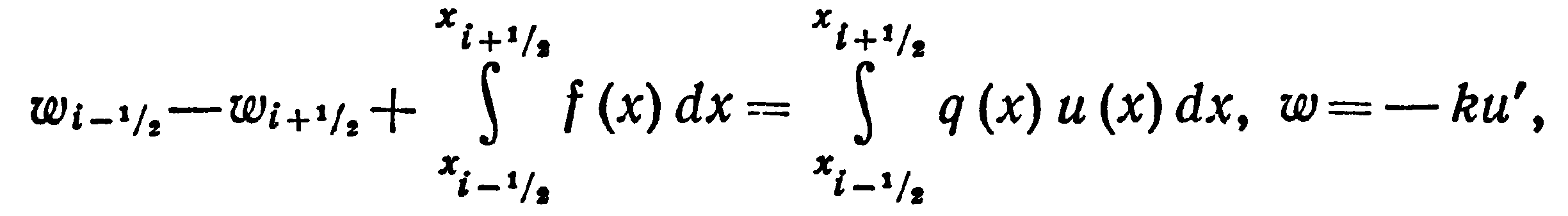
где
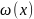 - поток тепла, q(x)
u(x)—мощность
стоков тепла (при q<
0— источников), пропорциональных
температуре, f(х)—плотность
распределения внешних источников
(стоков) тепла.
- поток тепла, q(x)
u(x)—мощность
стоков тепла (при q<
0— источников), пропорциональных
температуре, f(х)—плотность
распределения внешних источников
(стоков) тепла.
Сток
тепла происходит за счет теплообмена
с внешней средой, происходящего на
боковой поверхности стержня. Величина
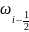 ,
дает количество
тепла, втекающее через сечение
,
дает количество
тепла, втекающее через сечение
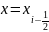 на отрезок
на отрезок
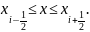
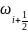 —количество
вытекающего через сечение тепла; третье
слагаемое в левой части дает количество
тепла, выделяющегося на отрезке
—количество
вытекающего через сечение тепла; третье
слагаемое в левой части дает количество
тепла, выделяющегося на отрезке
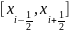 3a
счет распределенных с плотностью
3a
счет распределенных с плотностью
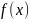 источников тепла, интеграл в правой
части есть количество тепла, отдаваемое
внешней среде за счет теплообмена на
боковой.
источников тепла, интеграл в правой
части есть количество тепла, отдаваемое
внешней среде за счет теплообмена на
боковой.
Чтобы
получить разностное уравнение, заменим
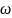 а интеграл, содержащий
а интеграл, содержащий
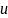 ,
линейными комбинациями значений
в
узлах сетки. Для этого воспользуемся
интерполяциями в окрестности узла
,
линейными комбинациями значений
в
узлах сетки. Для этого воспользуемся
интерполяциями в окрестности узла
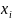 .
Возьмем простейшую интерполяцию
.
Возьмем простейшую интерполяцию

Где
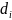 есть среднее значение
есть среднее значение
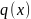 на отрезке
длины h.
Проинтегрируем равенство
на отрезке
длины h.
Проинтегрируем равенство
 на отрезке
:
на отрезке
:
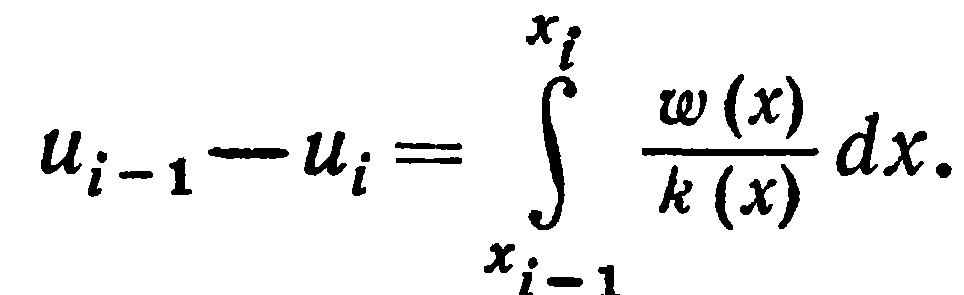
Предполагая,
что
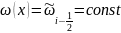 при
,
имеем
при
,
имеем
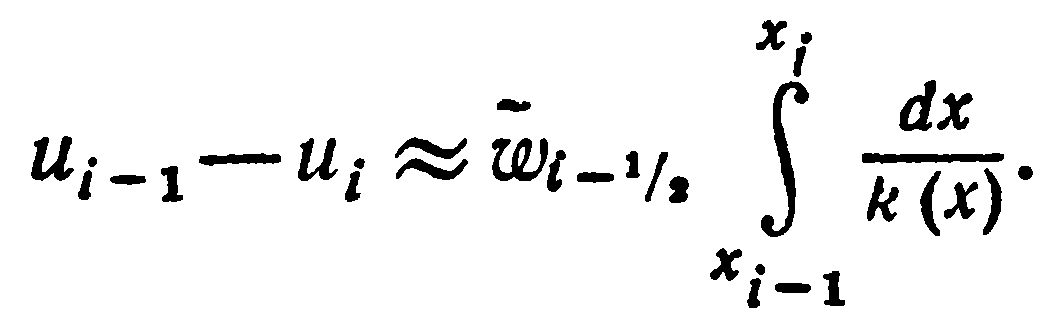
Отсюда
находим приближенное значение
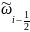 потока
потока
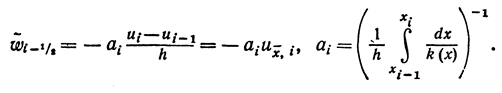
Отметим, что
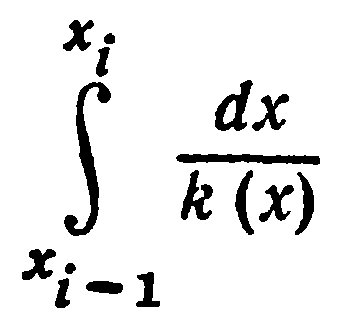 есть теплое
сопротивление отрезка
есть теплое
сопротивление отрезка
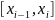 .
.
Подставляя
и обозначая через
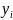 искомую функцию, получим консервативную
разностную схему
искомую функцию, получим консервативную
разностную схему