
- •Глава I. Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
- •Глава II. Численное моделирование теплового процесса приварки сварочной гильзы в полимерных армированных трубах
- •Введение Актуальность
- •Цель работы
- •Глава I Численное решение квазилинейных многомерных уравнений теплопроводности с разрывными коэффициентами
- •Однородные разностные схемы для уравнения теплопроводности
- •Сосредоточенный источник тепла
- •Цилиндрически-симметричные задачи теплопроводности
- •Квазилинейное уравнение теплопроводности
- •Метод суммарной аппроксимации
- •Методы решения задачи Стефана
- •Методы с выделением границы фазового перехода
- •Методы сквозного счета
- •Глава II Численное моделирование теплового процесса приварки сварочной гильзы в полимерных армированных трубах
- •Постановка задачи
- •Алгоритм задачи Стефана
- •Решение задачи теплопроводности по радиальной переменной
- •Решение задачи теплопроводности по осевой переменной
- •Заключение.
- •Список использованной литературы
Методы решения задачи Стефана
Задача о фазовом переходе
Важный класс нелинейных проблем теплообмена связан с процессами фазовых превращений. Мы рассматриваем переходы твердое тело—жидкость. Для моделирования процессов плавления/кристаллизации чистых веществ используется классическая модель Стефана, которая характеризуется заданием постоянной температуры на границе фазового перехода[24].
Пусть
имеются две фазы с коэффициентами
теплопроводности и теплоемкости
 ,
,
 и
и
 ,
,
 .
В каждой фазе температура удовлетворяет
уравнению
.
В каждой фазе температура удовлетворяет
уравнению
![]()
На
границе раздела фаз температура постоянна
и равна температуре фазового перехода,
 .
Скорость движения
.
Скорость движения
границы фазового перехода ξ удовлетворяет уравнению
![]()
если
в первой фазе
 ,
во второй
,
во второй
 .
.
Вводя σ-функцию, уравнение запишем в виде
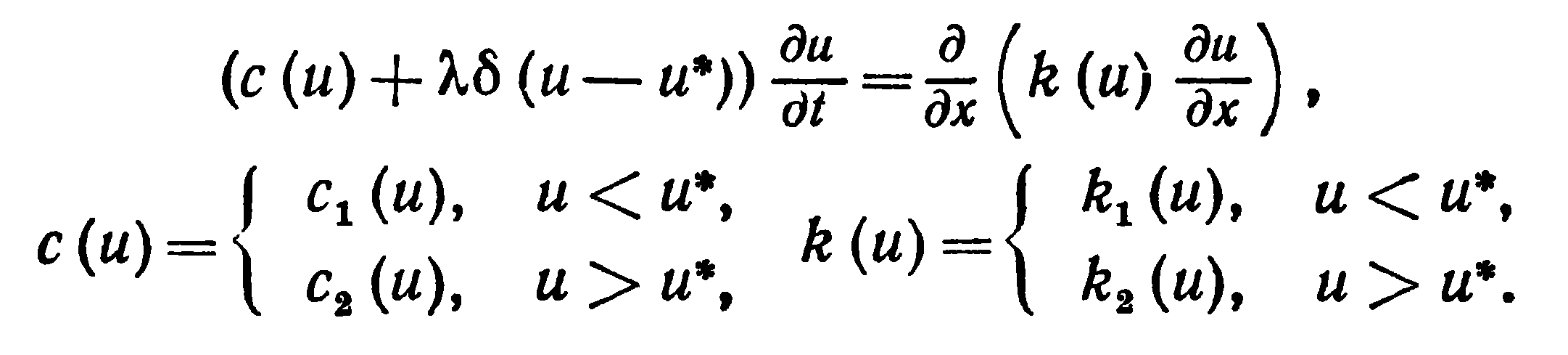
Методы с выделением границы фазового перехода
Модельная однофазная одномерная задача Стефана
Поясним
основные подходы к численному решению
задач типа Стефана с выделением границы
фазового перехода на примере простейшей
одномерной однофазной задачи Стефана.
Рассмотрим отрезок
 ,
который точкой
,
который точкой
 (граница фазового перехода),
(граница фазового перехода),
 разбивается на две подобласти:
разбивается на две подобласти:
![]()
Будем
считать температуру фазового перехода
равной нулю
 ,
поэтому в твердой фазе, которая занимает
область
,
поэтому в твердой фазе, которая занимает
область
 ,
положим
,
положим
 ,
а в жидкой (область
,
а в жидкой (область
 )
—
)
—
 .
Для определения температуры в жидкой
фазе рассматривается уравнение
теплопроводности (однородная среда)
.
Для определения температуры в жидкой
фазе рассматривается уравнение
теплопроводности (однородная среда)
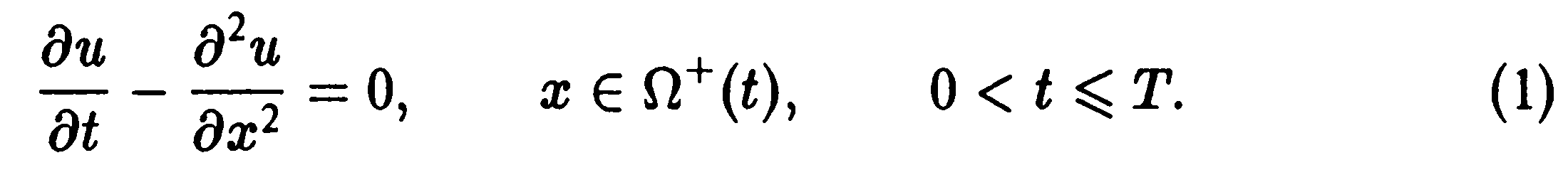
Дополним уравнение (1) начальным условием
![]()
Пусть левый конец поддерживается при заданной температуре:
![]()
На границе фазового перехода выполнены следующие условия:
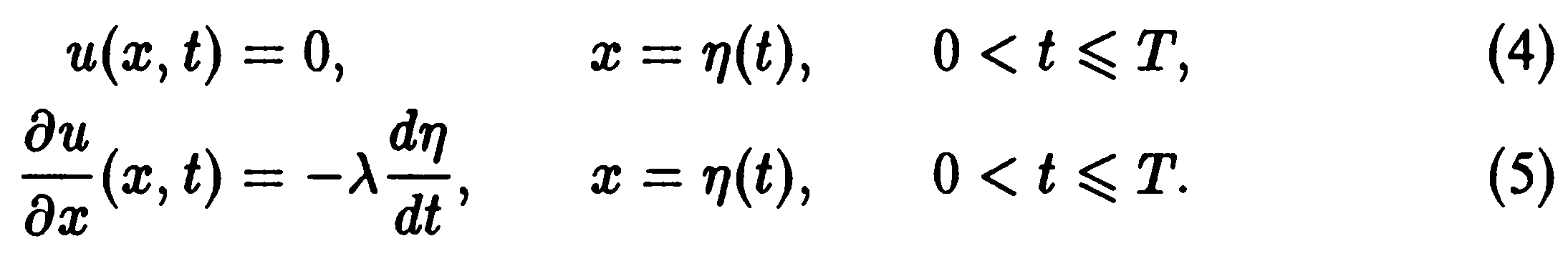
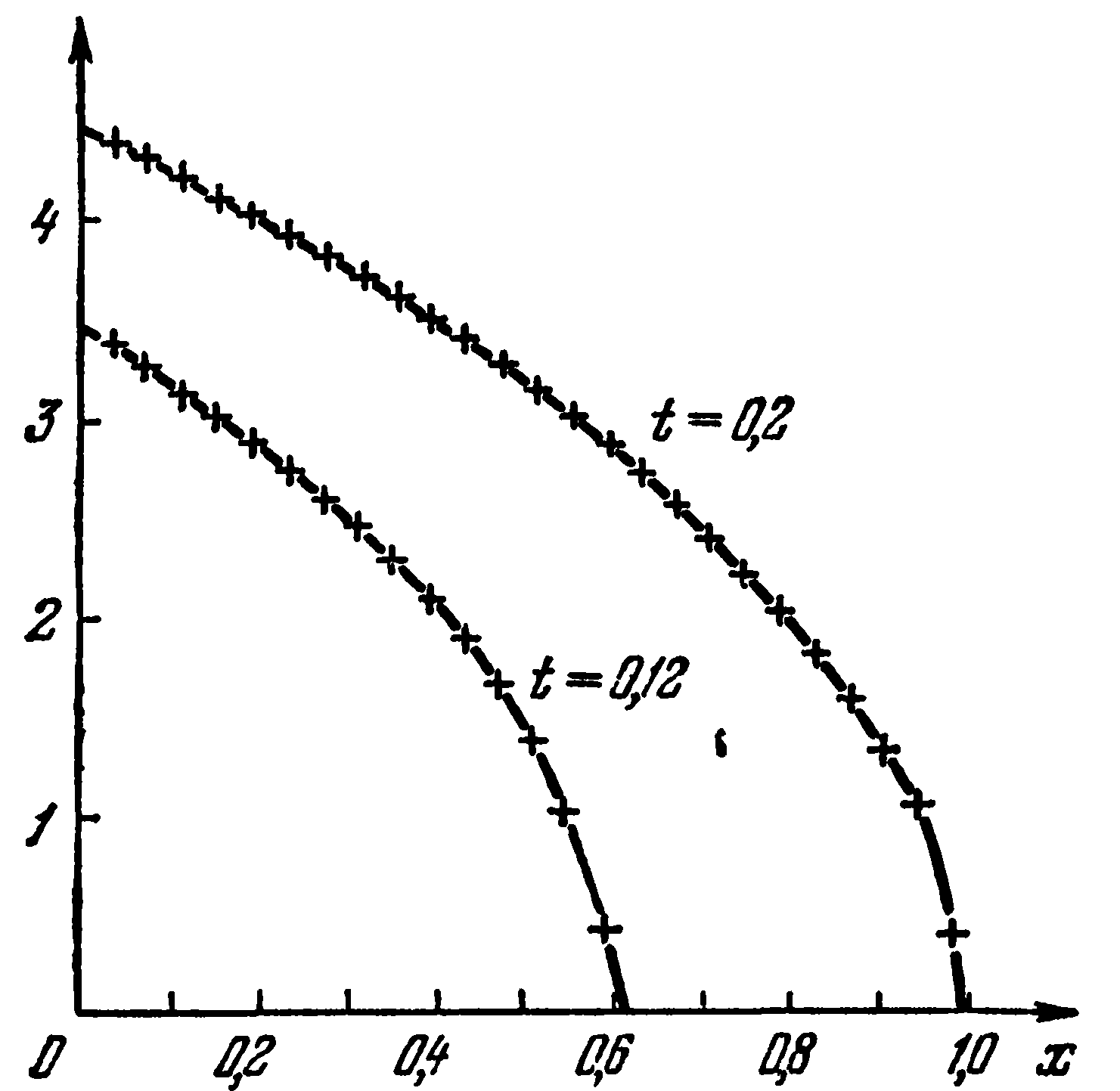
В
силу сформулированных предположений
о граничных и начальных условиях в
однофазной задаче Стефана (1)-(5) скорость
движения границы фазового перехода
положительна, т. е. область жидкой фазы
постепенно расширяется. Монотонное
возрастание функции
 следует
из принципа максимума для параболических
уравнений.
следует
из принципа максимума для параболических
уравнений.
Ловля фронта в узел пространственной сетки
Отметим некоторые простейшие вычислительные алгоритмы решения поставленной одномерной задачи (1)-(5) с учетом монотонного расширения области жидкой фазы. Рассматриваются методы с выделением границы фазового перехода, поэтому с неизвестной границей связывается узел расчетной сетки.
В
области
 ,
введем равномерную сетку с шагом h:
,
введем равномерную сетку с шагом h:
![]()
и пусть — множество внутренних узлов. По времени будем использовать неравномерную сетку
![]()
с
переменным шагом
 .
Следует выбирать шаг по времени
.
Следует выбирать шаг по времени
 ,
,
 таким,
чтобы за этот временной промежуток
таким,
чтобы за этот временной промежуток
 граница фазового перехода сдвинулась
ровно на один шаг пространственной
сетки. Этот подход известен как метод
ловли фронта в узел сетки.
граница фазового перехода сдвинулась
ровно на один шаг пространственной
сетки. Этот подход известен как метод
ловли фронта в узел сетки.
Метод выпрямления фронта
Для одномерной задачи (1)-(5) естественным является подход с использованием вместо х новой независимой переменной ξ, такой чтобы в новых переменных задача решалась в фиксированной области. Простейшая такая замена для задачи (1)-(5) имеет вид
![]()
Новая переменная ξ изменяется в фиксированных пределах от 0 (на левом конце х = 0) до 1 (на границе фазового перехода ) .При рассмотрении задач теплопроводности с фазовыми превращениями подходы с такими преобразованиями независимых переменных известны как методы выпрямления фронтов, так как в этом случае граница фазового перехода совпадает с фиксированной координатной линией.
