
- •Содержание
- •Виды моделей
- •Модель объекта управления
- •Моделирование
- •Построение модели.
- •Получение данных
- •Основные предпосылки мнк: а по мнк должно быть
- •Приведены в пример практические реализации в.Я. Ротыча.
- •Обработка экспериментальных данных
- •Выбор структуры модели
- •Параметрическое оценивание
- •Оценка соответствия полученной модели экспериментальным данным
- •Регрессионный анализ:
- •Имитационное моделирование с применением натурных данных
- •Проверка полезности модели с помощью целевого критерия
- •Проблема некорректности задачи идентификации
- •Имитационное моделирование
- •Общая структура
- •Отображения информации
- •Натурно-модельные обучающие комплексы
- •9.1. Обучающие системы на базе многовариантных структур
- •9.1.1. Структура многоканальной игровой обучающей системы
- •9.1.2. Особенности представления информации в обучающих системах
- •9.1.3. Простой вариант учебной нормативной модели (применительно к управленческим задачам )
- •9.2. Общие структуры тренажеров
- •9.3. Система освоения и исследования методов идентификации, прогнозирования, регулирования
- •9.4. Система освоения и исследования методов идентификации
- •Литературные источники
- •П рактические работы
- •Постановка задачи
- •Приложение 1
- •Постановка задачи Моделирование доменной плавки по каналу «влажность дутья – содержание кремния»
- •Решение
Имитационное моделирование с применением натурных данных
Натурные
данные получают из действующих систем
контроля по результатам пассивного,
активного или комбинированного
эксперимента. Главное здесь в том, что
необходимо с комбинацией этих данных
отобразить все основные особенности и
условия функционирования объекта. Если
эти условия могут существенно изменится,
то, как правило, экспериментальные
данные будут отражать изменения этих
условий. Они (данные) будут характеризоваться
различными статистическими свойствами,
в частности, различен и характер изменения
тренда (опорного уровня): постоянный,
линейный, более сложный полиноминальный
тренд; различная изменчивость около
этих уровней. Чем больше изменчивость
условий, тем больше нужно набрать таких
групп данных, внутри которых их
статистические свойства примерно
одинаковы Но каждая группа друг от друга
будет отличаться характером изменения
тренда, изменчивостью около тренда и
т.д. Причем в каждой группе должно быть
не менее двух выборок, одна из них должна
быть обучающей, а другие – контрольные.
На обучающей выборке с помощью методов
оптимизации, например поисковых процедур,
осуществляется настройка параметров
модели, а если это необходимо и ее
структуры. Чаще всего в качестве начальных
оценок искомых параметров модели при
такой настройке берут значения, полученные
расчетным путем с использованием,
например, метода наименьших квадратов.
Полученные модели на обучающих выборках
проверяются затем на контрольных, то
есть для каждой выборки рассчитывается
критерий точности. На контрольных
выборках точность всегда ниже, чем на
обучающих. Если обучающих выборок
несколько в каждой группе, то результат
исследования выразится в конкретном
диапазоне значений критерия. Такая
процедура повторяется для каждой группы
выборок данных. Это связано с тем, что
эффективность проверяемых с помощью
имитационного моделирования моделей,
алгоритмов, систем должна оцениваться
многократно, поскольку эффективность
такой процедуры аналитически не доказана.
В качестве критериев эффективности
моделирования используют: точностные
(среднемодульные, среднеквадратические)
и критерии воспроизводимости (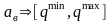 ). Критерий воспроизводимости может
быть выражен через диапазон изменения
точностных критериев. Чем меньше этот
диапазон, тем воспроизводимость
результатов лучше.
). Критерий воспроизводимости может
быть выражен через диапазон изменения
точностных критериев. Чем меньше этот
диапазон, тем воспроизводимость
результатов лучше.
Проверка полезности модели с помощью целевого критерия
В этом случае модель, построенная методами идентификации, проверяется с помощью целевого критерия. И если путем, например, имитационного моделирование будет показано с помощью целевого критерия, что конечный результат лучше, чем без этой модели, то модель можно считать полезной и использовать ее для решения этой конкретной задачи. Например, построенная модель используется в задаче управления, причем в состав алгоритма управления такая модель используется в явном виде. В данном случае целесообразно проверять не только повышение уровня целевого критерия, но и воспроизводимость его значений при функционировании системы для различных условий, т.е. в этом случае, как и в первом, используется моделирование, причем на множестве выборок многократно
Рассмотренные выше методы идентификации относятся к построению статических моделей, т.е. модели без учета времени. Классические методы идентификации объекта с помощи динамических моделей были даны в ТАУ раздел получение и обработка кривых разгона. Кроме этого, для этой цели также используются динамический корреляционный анализ, где оцениваются весовые или импульсные функции. Этот раздел находится на страницах 61 – 71. Следует понимать, что метод нельзя применять для управляемых объектов. В принципе его можно использовать выполнение, некоторых условий или активности эксперимента. Для такого случая исследования воздействий, должны изменять скачки или импульса, в виде случайного процесса или случайной функции.
Идентификация линейных динамических систем методами пассивного эксперимента (для ОУ не применим)
Основное уравнение идентификации и методы его решения
Одной из наиболее распространенных форм математического описания линейных динамических объектов в непараметрической форме является весовая, или импульсная переходная функция g(t). Эта характеристика однозначно описывает динамические свойства объекта.
Рассмотрим линейную динамическую систему с одним входом и выходом. Выход объекта y(t) связан со входом x(t) некоторым оператором А.
Представим
x(t)
в виде разложения по системе
 -функций;
-функций;
X(t)=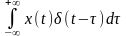 (82)
(82)
Здесь
(t
-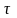 )
-
-функция, действующая в момент времени,
равный
.
Поскольку рассматриваемая система
линейна, для нее справедлив принцип
суперпозиции:
)
-
-функция, действующая в момент времени,
равный
.
Поскольку рассматриваемая система
линейна, для нее справедлив принцип
суперпозиции:
A (83)
(83)
Поскольку y(t)=Ax(t), то
y(t)=A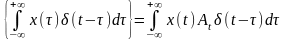 (84)
(84)
Здесь
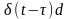 =g(t,
)
– реакция объекта на
-функцию,
т.е. импульсная переходная функция.
=g(t,
)
– реакция объекта на
-функцию,
т.е. импульсная переходная функция.
Если сигнал на входе системы появляется, начиная с момента t=0, выражение (71) примет вид
Y(t)
=
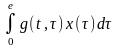 (85)
(85)
Дли стационарных объектов интеграл-свертки записывается следующим образом:
Y(t)= (86)
(86)
Установим связь между статистическими характеристиками объекта управления. Известно, что взаимная корреляционная функция стационарного случайного процесса определяется по формуле
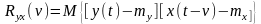 (87)
(87)
Подставим в (74) значение y(t) из (73) :
Rxy( )=
)= (88)
(88)
Учитывая,
что
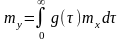 ,получим:
,получим:
Ryx(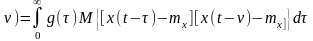 (89)
(89)
Т.к.
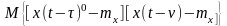 есть
автокорреляционная функция входного
сигнала R
есть
автокорреляционная функция входного
сигнала R (
( )
) ,
то в итоге запишем следующее уравнение:
,
то в итоге запишем следующее уравнение:
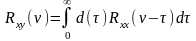 (90)
(90)
Это уравнение называют основным уравнением идентификации [5] или уравнением Винера-Хопфа. При выводе уравнения (77) рассматривались центрированные входные и выходные сигналы, мат.ожидание которых равно нулю. Однако уравнение (77) справедливо и для нецентрированных сигналов x(t) и y(t), т.е. содержащих неслучайную составляющую.
Пусть
входной сигнал x(t)
представляет собой белый шум.
Автокорреляционная функция белого шума
является
функцией.
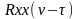 =
=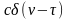 , где с
–известная постоянная величина,
характеризующая спектральную плотность
белого шума. Тогда в соответствии со
свойствами
- функции получим:
, где с
–известная постоянная величина,
характеризующая спектральную плотность
белого шума. Тогда в соответствии со
свойствами
- функции получим:
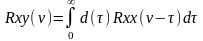 =
=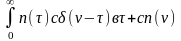 ;
(91)
;
(91)
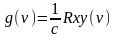 .
(92)
.
(92)
Таким образом, взаимная корреляционная функция выходного и входного сигналов объекта в случае, когда входной сигнал является белым шумом, пропорциональна импульсной функции переходной функции объекта.
Рассмотрим влияние помех при измерении сигналов x(t) и y(t) на определение импульсной переходной функции. Вначале будем считать, что с помехой измеряется только входной сигнал
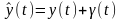 .
(93)
.
(93)
Тогда
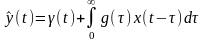 .
(94)
.
(94)
Умножив
(81) на x(
t-
)
и усреднив результат на интервале Т,
Т ,
получим:
,
получим:
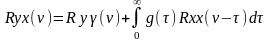 .
(95)
.
(95)
Наличие
помехи привело к тому, что в уравнении
Винера-Хопфа появилось дополнительное
слагаемое
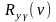 -
взаимокорреляционная функция сигнала
-
взаимокорреляционная функция сигнала
 и помехи
и помехи
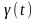 .
.
Для того, чтобы помеха не сказалась на результате идентификации, требуется, чтобы =0, т.е. помеха и выходной сигнал были некоррелированны.
Пусть
сигнал y(t)
измеряется без помех, а входной сигнал
измеряется с помехой
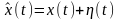 .
При этом имеет место соотношение
.
При этом имеет место соотношение
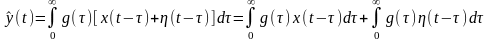 (96)
(96)
Умножив
(83) на [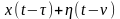 ]
и усреднив результат по времени, получим:
]
и усреднив результат по времени, получим:

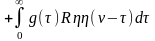 (97)
(97)
Для
большинства реальных объектов можно
считать, что помехи измерения являются
некоррелированными с результатом
измерения и кроме того, значения входного
сигнала некоррелированны с помехами
при измерении x(t).
Тогда
 0;
0;
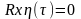 ;
;
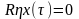 и уравнение (83) примет вид
и уравнение (83) примет вид
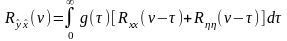 ;
(98)
;
(98)
Из этого уравнения видно, что помеха на входе приводит к ошибкам в определении весовой функции. Этот же вывод можно распространить на случай, когда с помехой измеряется и входной, и выходной сигналы.
Уравнение Винера-Хопфа относится к классу интегральных уравнений Фретгольма I рода. В общем случае такое уравнение записывается в виде
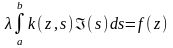 ,
(99)
,
(99)
где
 - параметр; в уравнении идентификации
=
I;
- параметр; в уравнении идентификации
=
I;
k(z,s)-ядро уравнения; в уравнении идентификации ядром уравнения является корреляционная функция;
 искомая
функция (импульсная весовая функция);
искомая
функция (импульсная весовая функция);
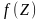 -
свободный член (взаимнокорреляционная
функция Ryx(
)).
-
свободный член (взаимнокорреляционная
функция Ryx(
)).
Для решения уравнения идентификации могут быть применены методы, разработанные в теории интегральных уравнений и в вычислительной математике для решения интегральных уравнений Фретгольма I рода [4.13].
Одним из наиболее простых методов решения (90) является конечно-разностный метод. Заменим бесконечный верхний предел у интеграла и уравнении Винера-Хопфа конечной величиной Т:
 (100)
(100)
Применим один из методов численного интегрирования – метод прямоугольников. Тогда (87) запишется в виде
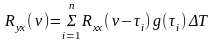 ,
(101)
,
(101)
где
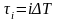 ;
;
Учитывая,
что
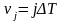 ,
,
 ,
представим уравнение (88) в векторно-матричной
форме:
,
представим уравнение (88) в векторно-матричной
форме:
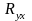 =
=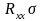 .
(102)
.
(102)
Здесь
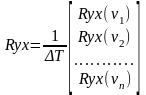 ;
(103)
;
(103)
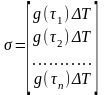 ;
(104)
;
(104)
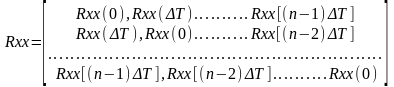 (105)
(105)
Рассмотрим как образуются элементы матрицы Rxx:
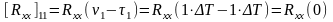 ,
(106)
,
(106)
т.е. дисперсия выходного сигнала
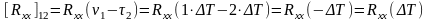 ,
(107)
,
(107)
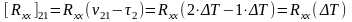 и
т.п. (108)
и
т.п. (108)
Из уравнения (89) находим:
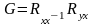 (109)
(109)
При решении этого уравнения на ЭЦВМ для обращения матрицы пользуются стандартными подпрограммами (СП). В библиотеках СП часто имеются несколько подпрограмм обращения матриц, работающих по разным алгоритмам. Алгоритмы вычисления обратных матриц описаны в литературе по численным методам.
Рассмотрим
аналог уравнения Винера-Хопфа для
дискретного случая. Допустим, что
измерения сигналов на входе и выходе
линейного динамического объекта
производятся с постоянным шагом
квантования
 Тогда уравнение (96) можно записать в
виде
Тогда уравнение (96) можно записать в
виде
 ,
(110)
,
(110)
где i-невязка (иногда называемая шумом).
Невязка состоит из реакций на другие входы системы и ошибок в линейной модели, возникающих из-за предположения, что объект линейный и стационарный, а так же из-за замены интегрального уравнения дискретной суммой.
Пусть i=k,k+1,….,N, причем N-k >k. Запишем уравнение (110) в развернутом виде:
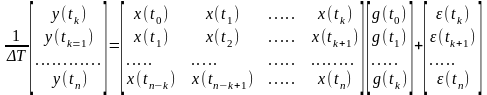 (111)
(111)
или в символическом виде:
Y=XG+E. (112)
Оценим вектор G из условия
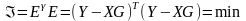 .
(113)
.
(113)
Необходимым
условием минимума
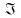 является
является
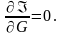 (114)
(114)
Из этого условия получаем уравнение Винера-Хопфа в дискретной форме:
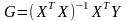 (115)
(115)
Матрица ХтХ представляет собой квадратную матрицу размером (х+1)*(к+1). Элементы ее определяются следующим образом:
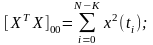 (116)
(116)
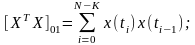 (117)
(117)
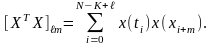 (118)
(118)
