Пример 1.

Пусть R(0,) – ПДС , статистика T=max_i<nx_i, но она смещенная.

Пусть T₁=-несмещенная

D(T₁)= D_T=,нарушено условие регулярности для равномерного распределения, т.к. область зависит от , тогда нельзя говорить о дифференцируемости p/

Т.е. такие распределения не очень хороши для оценивания

Такое явление, когда дисперсия убывает быстрее, чем ¹/_n, называется суперэффективным

Не всегда существует оценка : в неравенстве Рао-Крамера достигается равенство.

Рассмотрим ситуацию : D_>(g’())²/I()

но  k-мерный =(₁,…,_k)

Будем понимать под g’() – градиент из частных производных.

g'()=)

под I() понимаем : I()=

I()=

i_m,n=,тогда дисперсия D_T>¹/_ng'()I^-1()(g'())^T

Пример 2.

N(m,²)

Пусть существует выборка из нормального распределения оценивать надо скалярные величины, будем оценивать m,²

Надо посчитать информацию матрицы Фишера

p(x,)=

ln p(x,)=

==

=====

т.е.

i₁₂=i₂₁=E((=0,т.к. перемножаются либо 1, либо 3 моменты.

I=, I^-1=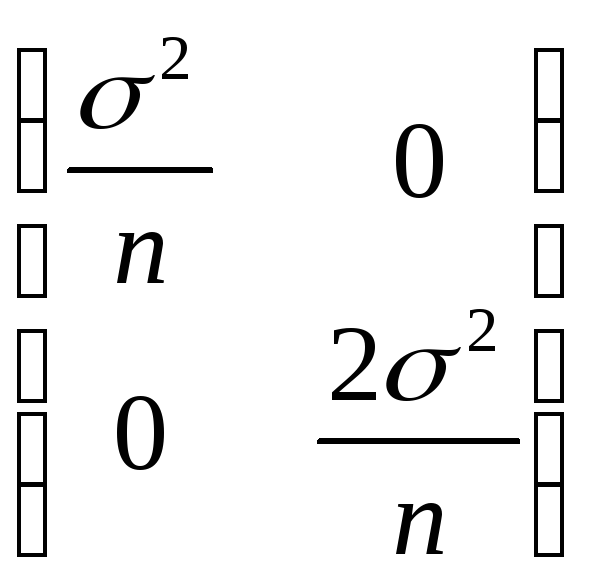,т.е. по Неравенству Рао-Крамера

D_T>2²/n

g'()=(0,1)

D_T>g'()I^-1()g()/n

Всегда ли достигается равенство

Пусть существует эффективная оценка S²=

Посчитаем дисперсию оценки:

DS²=

Границы не совпадают

=> этом примере ни при каких n не достигается равенство в неравенстве Рао-Крамера

Если какой-то параметр знаем, то равенство достигается

Пример 3.

Пусть m известно

Можно показать, что дисперсия такая же

S²=, дисперсия этой S²

DS²=

Пусть Распределение Пуассона

P(X=k) =k=0,1,2…

I₁()======

Получается дисперсия любой оценки DT>^/_n

Dx=^/_n, т.е. равенство достигается.

Для печати шпор

2,4,6,8,10,12,14,16,18,20,22,24,26,27,30,36,32,33,36,36

5,36,9,7,13,11,17,15,21,19,25,23,28,29,36,31,34,35,36,36