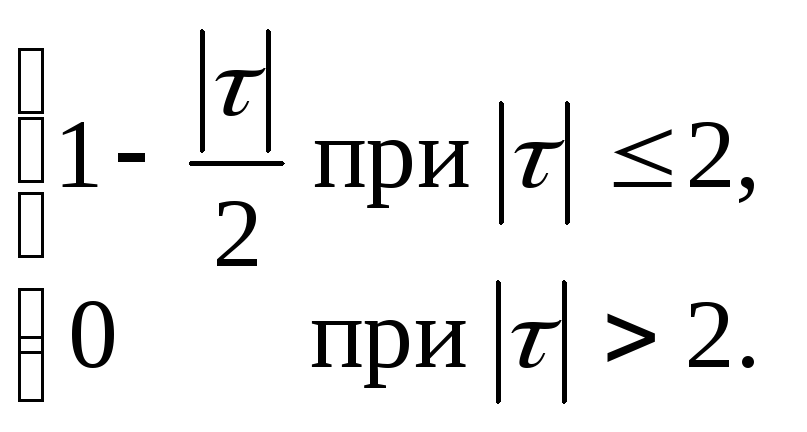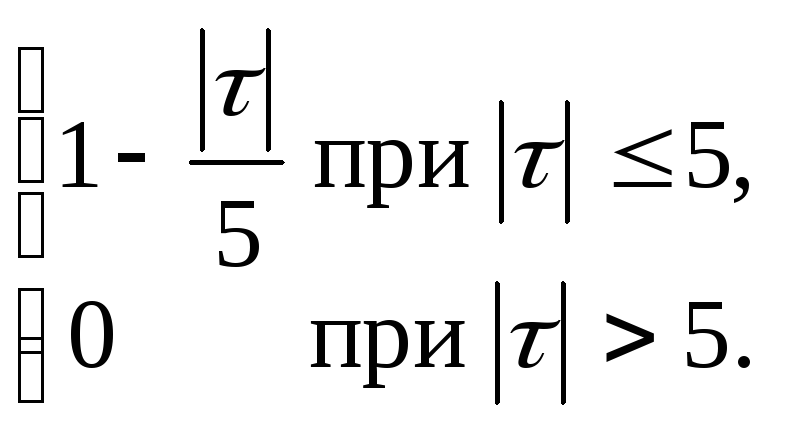19

Министерство образования Российской Федерации

ЮЖНО-РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ЭКОНОМИКИ И СЕРВИСА

(ЮРГУЭС)

З А Д А Ч И

“Элементы теории случайных процессов”

для студентов 2 – 3 курсов радиотехнических специальностей

Шахты 2002

Составитель

Син Л.И. Доцент кафедры математики ЮРГУЭС

Рецензент

Шрайфель И.С. Доцент кафедры математики ЮРГУЭС,

канд. физико-математических наук

Сборник содержит 15 расчетных заданий по корреляционной теории случайных процессов, включенных в типовой расчет по теме “Элементы теории случайных процессов”. Эта тема изучается студентами радиотехнических специальностей в курсах «Высшая математика» и «Специальные разделы математики». В известных сборниках заданий по типовому расчету /1, 2/ нет заданий на эту тему. Задания 17 относятся к вычислению характеристик случайных процессов общего вида, их производных и интегралов. Задания 8 12 посвящены вычислению характеристик стационарных (в широком смысле) случайных процессов. Задания 13 15 относятся к вопросу преобразования стационарных случайных процессов при прохождении через стационарную линейную динамическую систему.

© Южно-Российский государственный университет экономики и сервиса, 2002

© Син Л.И., 2002

Содержание

РАСЧЕТНЫЕ ЗАДАНИЯ……………………………..…………………………..4

Обозначения ……………………...………………………………………………..4

Задание 1………………..………….……………………………….……………4

Задание 2………………..………….……………………………….……………5

Задание 3………………..………….……………………………….……………6

Задание 4………………..………….……………………………….……………7

Задание 5………………..………….……………………………….……………8

Задание 6………………..………….……………………………….……………9

Задание 7………………..………….……………………………….………..…10

Задание 8………………..………….……………………………….…………..10

Задание 9………………..………….……………………………….…………..11

Задание 10………………..………….……………………………….…………12

Задание 11………………..………….……………………………….…………13

Задание 12………………..………….……………………………….…………14

Задание 13………………..………….……………………………….…………15

Задание 14………………..………….……………………………….…………17

Задание 15………………..………….……………………………….…………18

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………………..20

Расчетные задания

Обозначения.

U N(m;) означает, что случайная величина U распределена по нормальному закону с математическим ожиданием m и дисперсией .

UR(a; b)  случайная величина U распределена равномерно на отрезке [a; b].

UE(λ)  случайная величина U распределена по экспоненциальному закону с параметром λ.

UВ(n, p)  случайная величина U распределена по биномиальному закону с параметрами с параметрами n (число испытаний), p (вероятность “успе-ха”).

UР(λ)  случайная величина U распределена по закону Пуассона с параметром λ.

ЗАДАНИЕ 1. Найти математическое ожидание m_X(t), корреляционную функцию К_X (t₁,t₂), дисперсию D_X (t) случайного процесса Х(t). U, V  некоррелированные случайные величины.

1.1. Х(t) = t² U + V cost  sint. U N(3; 2), V E(0.5).

1.2. Х(t) = t U – 3е^3t V + cost. U R(0; 6), V B(10; 0.5).

1.3. Х(t) = e^t U – V cht + 3. U P(0.2), V R(–2; 2).

1.4. Х(t) = U sint  V t + t⁵. U N(1; 2), V P(2).

1.5. Х(t) = t³ U – V cos t – 2. U R(–1; 3), V E(0.4).

1.6. Х(t) = 3 U sht – е^3tV + cost. U E(0.25), V R(2; 4).

1.7. Х(t) = 3 + U sin2t – 4t V. U B(10; 0.3), V P(3).

1.8. Х(t) = U cos3t – V sint – t. U R(–3; 1), V N(–1; 0.5).

1.9. Х(t) = t² U – V cht + t². U E(0.1), V B(20; 0.2).

1.10. Х(t) = е^t U  V sint + t. U N(–2; 2), V E(4).

1.11. Х(t) = е^3t U – V t + 2t. U R(–3; 3), V B(10; 0.6).

1.12. Х(t) = 3Usint – V е^t – е^t. U P(4), V R(1; 3).

1.13. Х(t) = t² – е^2t U – V t. U N(–1; 0.7), V E(0.5).

1.14. Х(t) = t U – V sin2t + 4t². U R(3; 6), V N(2; 3).

1.15. X(t) = U cos3t – V t² + 3. U P(5), V R(–3; 5).

1.16. Х(t) = 5t + 3t²U – V е^2t. U N(–2; 1.5), V E(0.2).

1.17. Х(t) = 5 + U sint – V t². U B(10; 0.1), V N(3; 0.3).

1.18. Х(t) = t² U – V cht + t. U P(2), V R(–2; 4).

1.19. Х(t) = t + U sh2t – 2t V. U N(–1; 2), V E(1/3).

1.20. Х(t) = t U – V sint + cost. U R(–2; 2), V B(20; 0.4).

1.21. Х(t) = е^–t + U cost – V t. U E(1/4), V R(–5; –1).

1.22. Х(t) = –t  U cht + V cost. U N(5; 2), V P(3).

1.23. Х(t) = t² U – V t – е^3t. U R(3; 6), V B(20; 0.5).

1.24. Х(t) = 3sint + 2U sht – V е^t. U E(2), V R(–1; 5).

1.25. Х(t) = U cos2t  V t – 4t. U P(2), V N(3; 0.3).

ЗАДАНИЕ 2. Найти корреляционную функцию К_Z (t₁, t₂) и дисперсию D_Z (t), если X(t), Y(t) – некоррелированные случайные процессы и даны корреляционные функции К_X (t₁,t₂), К_Y (t₁,t₂).

2.1. Z(t) = X(t)sintY(t)(t²+1)+e^t, K_x(t₁,t₂) =1/(1+|t₂–t₁|), K_y (t₁,t₂) =t₁t₂+1.

2.2. Z(t) = X(t)e^t Y(t) cost+e^2t, K _x(t₁,t₂) =K_y (t₁,t₂) =1/(1+(t₂–t₁)²).

2.3. Z(t) = X(t)tY(t) cost+sint, K_X(t₁,t₂) = 1/(1+|t₂–t₁|), K_Y (t₁,t₂) = cos(t₂–t₁).

2.4. Z(t) = X(t)sintt²Y(t)+e^t, K_X(t₁,t₂) = cos(t₂–t₁), K_Y (t₁,t₂) = 1/(t₁²t₂²).

2.5. Z(t) = X(t)cos3t(t+3)Y(t)+sint, K_X(t₁,t₂) = K_Y (t₁,t₂ ) = exp(–|t₂–t₁|).

2.6. Z(t) = X(t)e^3t–Y(t)sint–t, K_X(t₁,t₂) = 1+ cos(t₂–t₁), K_Y (t₁,t₂ ) = sint₂sint₁.

2.7. Z(t) = X(t)t+Y(t)e^2t–sht, K_X(t₁,t₂ ) = K_Y(t₁,t₂ ) = exp(–2|t₂–t₁|).

2.8. Z(t) = X(t)cost–(3t²+1)Y(t)+sint, K_X(t₁,t₂) = t₁²t₂², K_Y(t₁,t₂) = cos(t₂–t₁).

2.9. Z(t) = X(t)cht–3tY(t)+e^t, K_X(t₁,t₂ ) = 2+cos(t₂–t₁), K_Y(t₁,t₂ ) = t₁t₂+1.

2.10. Z(t) = t⁴X(t)–Y(t) cht+cht, K_X(t₁,t₂) = 2+t₁t₂,K_Y(t₁,t₂) = exp(–4|t₂–t₁|).

2.11. Z(t) = X(t) sht–Y(t)t+t, K_X(t₁,t₂ ) = cost₁cost₂, K_Y(t₁,t₂ ) = cos(t₂–t₁).

2.12. Z(t) = X(t)sint–e^tY(t)+e^t, K_X(t₁,t₂ ) = cos2(t₁–t₂), K_Y(t₁,t₂ ) = 2+t₁²t₂².

2.13. Z(t) = 2tX(t)– Y(t) sint+e^t, K_X(t₁,t₂ ) =exp(–t₁–t₂), K_Y(t₁,t₂ ) = cos(t₂–t₁).

2.14. Z(t) = e^tx(t)–2Y(t) cost–sint, K_X(t₁,t₂) = 2t₂t₁+1, K_Y(t₁,t₂ ) = cos3(t₂–t₁).

2.15. Z(t) = X(t)cost–t³Y(t)+sht, K_X(t₁,t₂) = 1+t₁t₂, K_Y(t₁,t₂) = exp(–2(t₂–t₁)²).

2.16. Z(t) = X(t) cht–tY(t)–t, K_X(t₁,t₂) = 9cos4(t₂–t₁), K_Y(t₁,t₂) = 1/((t₂–t₁)²+1).

2.17. Z(t) = X(t)sint–Y(t)cost+t, K_X(t₁,t₂) = 9t₁t₂ , K_Y(t₁,t₂) = cos2(t₂–t₁).

2.18. Z(t) = 4t²X(t)–Y(t)e^t–t, K_X(t₁,t₂) = sin2t₂sin2t₁, K_Y(t₁,t₂) = 4exp(–(t₂–t₁)²) .

2.19. Z(t) = e^–tX(t)–2tY(t)+sht, K_X(t₁,t₂) = 2+t₁t₂, K_Y(t₁,t₂) = 4/(1+2(t₂–t₁)²).

2.20. Z(t) = X(t) cost–t²Y(t)+t, K_X(t₁,t₂) = 1+t₁²t₂², K_Y(t₁,t₂) = cos4(t₂–t₁).

2.21. Z(t) = X(t)sint– e^tY(t)+e^t, K_X(t₁,t₂) = cost₁ cos t₂, K_Y(t₁,t₂) = 1/(1+2(t₂–t₁)²).

2.22. Z(t) = 2t²X(t)– Y(t) cht+e^t, K_X(t₁,t₂) = 1/exp(|t₂–t₁|), K_Y(t₁,t₂) = 1+3t₂t₁.

2.23. Z(t) = X(t) sin4t–2tY(t)–e^t, K_X(t₁,t₂) = 4exp(–2(t₂–t₁)²), K_Y(t₁,t₂) = cos(t₂–t₁).

2.24. Z(t) = e^tX(t)– Y(t) cost+sht, K_X(t₁,t₂) = 4+t₁t₂, K_Y(t₁,t₂) = 4exp(–2(t₂–t₁)²).

2.25. Z(t) = 2(t+1)X(t)– Y(t) sint+cost, K_X(t₁,t₂) =exp(–t₁–t₂), K_Y(t₁,t₂) = t₂t₁.

ЗАДАНИЕ 3. Z(t) = t² + g(t) X(t)  h(t) Y(t), где g(t), h(t) – неслучайные функции, X(t), Y(t) – центрированные случайные процессы с корреляционными функциями K_X = K_X (t₁,t₂), K_Y =K_Y (t₁,t₂) и взаимной корреляционной функцией K_XY = K_XY (t₁,t₂).

Найти математическое ожидание m_Z(t), корреляционную функцию K_Z(t₁,t₂), дисперсию D_Z(t), нормированную корреляционную функцию ρ_Z(t₁,t₂) случайного процесса Z(t).

3.1. g(t)=t², h(t)=e^t, K_X =exp(–t₁–t₂), K_Y =16exp(–t₁–t₂), K_XY =4exp(–t₁–t₂).

3.2. g(t)=e^–2t, h(t)=sin4t, K_X =4cos(t₁–t₂), K_Y =36cos(t₁–t₂), K_XY =12cos(t₁–t₂).

3.3. g(t)=t, h(t)=e^–t, K_X =4(1+t₁t₂), K_Y =9(1+t₁t₂), K_XY =6(1+t₁t₂).

3.4. g(t)=sinωt, h(t)=t, K_X =9cost₁cost₂, K_Y =25cost₁cost₂, K_XY =15cost₁cost₂.

3.5. g(t)=cosωt, h(t)=sinωt, K_X =9t₁t₂, K_Y =36t₁t₂, K_XY =18t₁t₂.

3.6. g(t)=t², h(t)=cos4t, K_X =25(2+|t₂–t₁|)^–1, K_Y =(2+|t₂–t₁|)^–1, K_XY =5(2+|t₂–t₁|)^–1.

3.7. g(t)=e^–3t, h(t)=3t, K_X =4exp(–|t₂–t₁|), K_Y =9exp(–|t₂–t₁|), K_XY =6exp(–|t₂–t₁|).

3.8. g(t)= sin6t, h(t)=e^t, K_X =4t₁t₂, K_Y =49t₁t₂, K_XY =14t₁t₂.

3.9. g(t)=t³, h(t)=sin2t, K_X =4sint₁sint₂, K_Y =16sint₁sint₂, K_XY =8sint₁sint₂.

3.10. g(t)=e^–2t, h(t)=cos4t, K_X =(t₁t₂)², K_Y =16(t₁t₂)², K_XY =4(t₁t₂)².

3.11. g(t)=cos2t, h(t)=sin2t, K_X =4(t₁t₂+1), K_Y =9(t₁t₂+1), K_XY =6(t₁t₂+1).

3.12. g(t)=e^–4t, h(t)=t, K_X =49cos2(t₁–t₂), K_Y =cos2(t₁–t₂), K_XY =7cos2(t₁–t₂).

3.13. g(t)=t, h(t)=sin2t, K_X =4(t₁t₂)³, K_Y =25(t₁t₂) ³, K_XY =10(t₁t₂) ³.

3.14. g(t)=t, h(t)=t², K_X =4/(1+|t₂–t₁|), K_Y =1/(1+|t₂–t₁|), K_XY =2/(1+|t₂–t₁|).

3.15. g(t)=–2t, h(t)=e^–4t, K_X =16cos(t₁–t₂), K_Y =25cos(t₁–t₂), K_XY =20cos(t₁–t₂).

3.16. g(t)=2t, h(t)=sin3t, K_X =(3+t₁)(3+t₂), K_Y =64(3+t₁)(3+t₂), K_XY =8(3+t₁)(3+t₂).

3.17. g(t)=e^t, h(t)=t⁴, K_X =4cos3(t₁–t₂), K_Y =9cos3(t₁–t₂), K_XY =6cos3(t₁–t₂).

3.18. g(t)=sin3t, h(t)=t, K_X =9cht₁cht₂, K_Y =49cht₁cht₂, K_XY =21cht₁cht₂.

3.19. g(t)=e^–2t, h(t)=t², K_X =16cos(t₁–t₂), K_Y =cos(t₁–t₂), K_XY =4cos(t₁–t₂).

3.20. g(t)=cht, h(t)=e^–2t, K_X =4sht₁sht₂, K_Y =16sht₁sht₂, K_XY =8sht₁sht₂.

3.21. g(t)=sh5t, h(t)=сh5t, K_X =exp(t₁+t₂), K_Y =9exp(t₁+ t₂), K_XY =3exp(t₁+t₂).

3.22. g(t)=e^t, h(t)=t², K_X =25sint₁sint₂, K_Y =4sint₁sint₂, K_XY =10sint₁sint₂.

3.23. g(t)=e^–t, h(t)=t, K_X =16cost₁cost₂, K_Y =cost₁cost₂, K_XY =4cost₁cost₂.

3.24. g(t)=sin10t, h(t)=cos10t, K_X =4(1+t₁t₂), K_Y =1+t₁t₂, K_XY =2(1+t₁t₂).

3.25. g(t)=t³, h(t)=e^2t, K_X =9t₁t₂, K_Y =25t₁t₂, K_XY =15t₁t₂.

ЗАДАНИЕ 4. Найти математическое ожидание m_Y (t), корреляционную функцию K_Y (t₁,t₂), дисперсию D_Y (t), нормированную корреляционную функцию ρ_Y (t₁,t₂) случайного процесса Y(t) = X(t), не дифференцируя X(t). Найти взаимную корреляционную функцию K_XY (t₁,t₂) и нормированную взаимную корреляционную функцию ρ_XY (t₁,t₂). U– случайная величина.

4.1. Х(t) = t 2– U е3t, U N(2;0.7).	4.2. Х(t)= Ut2 sint, U B(10;0.5).
4.3. Х(t) = U t – 4t2, U R(3;6).	4.4. Х(t) = U t3 – sint, U P(4).
4.5. Х(t) = Ucos3t–3, U P(5).	4.6. Х(t) =  U e2t – t, U P(2).
4.7. Х(t) = 3t2 + U е2t, U E(0.2).	4.8. Х(t) = U sint + t, U N(1;2).
4.9. Х(t) = 5t2  U sint. U B(10; 0.1).	4.10. Х(t) = U t3 – cost, U R(–1;3).
4.11. Х(t) = U t2 + cht. U R(–2;2).	4.12. Х(t) = U е3t + cost, U E(0.25).
4.13. Х(t) = t  U sh2t. U N(–1;2).	4.14. Х(t ) =3t U sin2t, U B(10;0.3).
4.15. Х(t)=U cost + t, U B(20; 0.4).	4.16. Х(t) = U cos3t – t, U R(–3;1).
4.17. Х(t) = U sht + е–t , U E(1/4).	4.18. Х(t) = U t2 – t2, U E(0.1).
4.19. Х(t) = U ch2t + cost, U P(3).	4.20. Х(t) = U еt + sint, U N(4;2).
4.21. Х(t) = U t2 – е3t, U R(3;6).	4.22. Х(t) = U е3t – 2t, U B(10;0.6).
4.23. Х(t) = 3sint  U е4t, U E(2).	4.24. Х(t) = 3U sint – еt, U P(2.5).
4.25. Х(t) = U cos2t – t, U N(3;0.8).

ЗАДАНИЕ 5. X(t) = f(t) + U g(t) + V h(t), где f(t), g(t), h(t)–неслучайные функции; U, V – некоррелированные случайные величины. Найти математическое ожидание m_Y (t), корреляционную функцию K_Y (t₁,t₂), дисперсию D_Y (t) случайного процесса Y(t) = t X(t) – 2X′(t), не дифференцируя X(t).

5.1. f(t) = e^2t, g(t) = t², h(t) = cos4t, U N(2,9), V E(0.2).

5.2. f(t) = cost, g(t) = e^–2t, h(t) = sin2t, U E(0.2), V R(–1;3).

5.3. f(t) = sin2t, g(t) = t, h(t) = e^–t, U B(10;0.3), V N(–1;2).

5.4. f(t) = t², g(t) = e^–3t, h(t) = sin3t, U P(2), V R(0;4).

5.5. f(t) = t³, g(t) = cost, h(t) = sint, U P(3), V N(–1;3).

5.6. f(t) = sin2t, g(t) = t, h(t) = cos4t, U R(–2;2), V B(20;0.1).

5.7. f(t) = cos4t, g(t) = e^–3t, h(t) = 3t, U P(3), V E(0.25).

5.8. f(t) = t²+2, g(t) = sin5t, h(t) = cos5t, U R(1;5), V B(20;0.4).

5.9. f(t) = 2t, g(t) = t³, h(t) = cos2t, U N(0;4), V P(1).

5.10. f(t) = –2t², g(t) = e^–2t, h(t) = cos2t, U R(–1;3), V P(2).

5.11. f(t) = t³+3, g(t) = cos2t, h(t) = sin2t, U N(–3;4), V B(10;0.4).

5.12. f(t) = t²–2, g(t) = e^–4t, h(t) = cos4t, U R(3;7), V P(4).

5.13. f(t) = 2t+1, g(t) = e^–3t, h(t) = sin3t, U P(2), V B(10;0.3).

5.14. f(t) = e^2t, g(t) = cos4t, h(t) = t², U N(10;4), V R(–3,3).

5.15. f(t) = cos4t, g(t) = 2t, h(t) = e^–4t, U E(0.5), V B(10;0.2).

5.16. f(t) = 1+e^–2t, g(t) = 2t, h(t) = sin5t, U R(–1;5), V P(0.8).

5.17. f(t) = sin2t, g(t) = e^t, h(t) = t², U P(5), V N(–5;3).

5.18. f(t) = cos3t, g(t) = sin3t, h(t) = ch3t, U R(–2;4), V B(20;0.4).

5.19. f(t) = t², g(t) = e^–2t, h(t) = sin2t, U P(3), V N(–3;2).

5.20. f(t) = sht, g(t) = ch2t, h(t) = e^–2t, U N(0;4), V R(1;7).

5.21. f(t) = t³, g(t) = ch6t, h(t) = sh6t, U P(4), V N(–2;5).

5.22. f(t) = sin2t, g(t) = t, h(t) = t², U R(–1;1), V B(10;0.6).

5.23. f(t) = cos2t, g(t) = e^–t, h(t) = t, U P(2), V E(0.5).

5.24. f(t) = t, g(t) = sin2ωt, h(t) = cos2ωt, U R(0;4), V B(10;0.7).

5.25. f(t) = sin2t, g(t) = t³, h(t) = cos2t, U N(10;4), V P(4).

ЗАДАНИЕ 6. X(t) = f(t) U, f(t)  неслучайная функция; U – cлучайная величина,

Найти математическое ожидание m_Z(t), корреляционную функцию К_Z(t₁,t₂), дисперсию D_Z (t), взаимные корреляционные функции K_ZX (t₁,t₂), K_XZ (t₁,t₂), не интегрируя X(t).

6.1. f(t) = cos6t, U E(0.2).	6.2. f(t) = 1/(1+t)2, U E(0.5).
6.3. f(t) = sin3t, U B(10;0.3).	6.4. f(t) = 1+e–2t, U B(20;0.4).
6.5. f(t) = e–3t, U P(2).	6.6. f(t) = e3t, U P(5).
6.7. f(t) = sin2t, U N(–1;3).	6.8. f(t) = 1/(2t+1), U R(–2;4).
6.9. f(t) = sh2t, U R(–2;2).	6.10. f(t) = 1/(1+t2), U N(–3;2).
6.11. f(t) = cos4t, U P(3).	6.12. f(t) = (1+t)2, U B(20;0.2).
6.13. f(t) = t2+t, U E(0.4).	6.14. f(t) = ch5t, U E(0.25).
6.15. f(t) = t3–1, U N(0;4)	6.16. f(t) = (1–t)3, U R(–1;1).
6.17. f(t) = –2t2, U R(–1;3).	6.18. f(t) = e–t, U P(6).
6.19. f(t) = 4t3+2t, U B(10;0.4).	6.20. f(t) = 3(1+t)2, U B(10;0.7).
6.21. f(t) = e–4t, U R(3;7).	6.22. f(t) = 1/(2t–3), U N(10;4).
6.23. f(t) = sh5t, U P(4).	6.24. f(t) = 1e5t, U E(0.75).
6.25. f(t) = ch3t, U N(10;4).

ЗАДАНИЕ 7. X(t)  случайный процесс,

Найти корреляционную функцию К_Y (t₁,t₂), дисперсию D_Y (t), нормированную корреляционную функцию ρ_Y (t₁,t₂) случайного процесса Y(t) = X(t) + Z(t), не интегрируя X(t). U – случайная величина.

7.1. x(t) = U ch3t, U P(2).	7.2. X(t) = U sin2ωt, U E(0.2).
7.3. X(t) = U / (1+ t)2, U N(10;4).	7.4. X(t) = U e–3t, U B(10;0.3).
7.5. X(t) = U (1et), U E(0.5).	7.6. X(t) = U sinωt, U N(0;4).
7.7. X(t) = U sin3t, U B(20;0.4).	7.8. X(t) = U sh2t, U N(–1;3).
7.9. X(t) = U/(2t + 1), U P(5).	7.10. X(t) = U cos4t, U R(–2;2).
7.11. X(t) = U/(1+ t2), U R(–2;4).	7.12. X(t) = U (t2+t), U P(3).
7.13. X(t) = U (1+ t)2, U N(–3;2).	7.14 X(t) = U (t3–1), U E(0.4).
7.15. X(t) = U chωt, U E(0.25).	7.16. X(t) = –2U t2, U N(10;4).
7.17. X(t) = U (1– t)3, U B(20;0.2).	7.18. X(t) = U (4t3+2t), U R(–1;3).
7.19. X(t) = U e–2t, U R(–1;1)	7.20. X(t) = U e–4t, U B(10;0.4).
7.21. X(t) = U (1+t)2, U P(6).	7.22. X(t) = U sh2t, U R(3;7).
7.23. X(t) = U/(2t–3), U B(10;0.7).	7.24. X(t) = U ch3t, U P(4).
7.25 X(t) = U cosωt, U N(10;4).

ЗАДАНИЕ 8. Доказать, что случайный процесс X(t) стационарен в широком смысле. Проверить свойство эргодичности для математического ожидания, корреляционной функции. Найти дисперсию случайного процесса. U, V  некоррелированные случайные величины.

8.1. Х(t) = (U 2)cos3t – Vsin3t, U R(0;4), V.

8.2. Х(t) = (U +2)cos2t – Vsin2t, U N(2;2), V.

8.3. Х(t) = Ucos5t – (V 5)sin5t, U R(4;4), V .

8.4. Х(t) = (U  4)cos8t – Vsin8t, U P(4), V N(0;2).

8.5. Х(t) = (U1)cos20t– Vsin20t, U E(1), V N(0;1).

8.6. Х(t) = (U2)cos11t – (V8)sin11t, U B(10;0.2), V B(10;0.8).

8.7. Х(t) = (U 1)cos6t – (V  4/3)sin6t, U R(1;3), V P(4/3).

8.8. Х(t) = U cos21t – (sin21t, U R(1;1), V .

8.9. Х(t) = (U8)cos15t + Vsin15t, U B(20;0.4), V .

8.10. Х(t) = U cos5t – (V5)sin5t, U R(2;2), V .

8.11. Х(t) = (U +10)cos2t – Vsin2t, U N(10;3), V N(0;3).

8.12. Х(t) = (U +4)cos7t – (V 9)sin7t, U N(4;3), V P(9).

8.13. Х(t) = (U 5)cos3t – Vsin3t, U E(0.2), V N(0;5).

8.14. Х(t) = (U2) cos12t– (V1.6)sin12t, U B(10;0.2), V P(1.6).

8.15. Х(t) = (U3)cos4t – (V3)sin4t, U P(3), V P(3).

8.16. Х(t) = (U 6)cos7t – (V 1)sin7t, U N(6;1), V P(1).

8.17. Х(t) = (U 2.5)cos11t – (V1)sin11t, U E(0.4), V N(1;2.5).

8.18. Х(t) = (U 5)cos2t– (V 25)sin2t, U E(0.2), V P(25).

8.19. Х(t) = U cos19t – (V )sin19t, U R(3;3), V

8.20. Х(t) = U cos6t – (V 4)sin6t, U R(2;2), V R(2;6).

8.21. Х(t) = (U 4) cos15t + V sin15t, U B(10;0.4), V .

8.22. Х(t) = U cos18t– (V+10)sin18t, U N(0;4), V N(10;4).

8.23. Х(t) = U cos4t – (V12)sin4t, U R(6;6), V P(12).

8.24. Х(t) = (U2)cos22t + (V4)sin22t, U E(0.5), V P(4).

8.25. Х(t) = (U 2)cos10t – (V2)sin10t, U E(0.5), V E(0.5).

ЗАДАНИЕ 9. k_X (τ)  корреляционная функция стационарного случайного процесса X(t). Найти корреляционную функцию, дисперсию производной X′(t), взаимную корреляционную функцию k_{XX } (τ).

9.1. kX (τ) = 5 (1  sin3τ2)exp(2τ2).	9.2. kX (τ) = (1 +2sin|τ|) exp(2τ2).
9.3. kX (τ) = 10 (1 + 2sin|τ|) exp(2|τ|).	9.4. kX (τ) = 8cos4τ / (2 + 6τ2).
9.5. kX (τ) = 5/ (1 + 2τ2 + 3τ4).	9.6. kX (τ) = 1/ (10 + 5τ2).
9.7. kX (τ) = 5 + 6cosτ cos3τ.	9.8. kX (τ) = 5(1  sin3τ 2) exp(2τ 2)
9.9. kX (τ) = 4 (1 + sinτ 2) exp(2τ 2).	9.10. kX (τ) = 5cos2τ / (1 +10τ 2).
9.11. kX (τ) = 1 + 8exp(9τ 2).	9.12. kX(τ)=10 (1+2|sinτ|)exp(2|τ|).
9.13. kX (τ) = (1 + sin|τ|) exp(|τ|).	9.14. kX (τ) = 10 +2 cos5τ cos3τ.
9.15. kX (τ) = 4cos2τ cos6τ.	9.16. kX (τ) = 2 (1  2τ2) exp(τ2)
9.17. kX (τ) = 3 (13sin2τ) exp(τ2).	9.18. kX (τ) = 1+ 6cosτ cos3τ.
9.19. kX (τ) = (1+|sin3τ|) exp(2|τ|).	9.20. kX (τ) = 5 (1+|τ|) exp(|τ|).
9.21. kX (τ) = 10/ (1+ 8τ 2 + τ4).	9.22. kX (τ) = 5/ (1 + 10τ2).
9.23. kX (τ) = 6 (1 + τ2) exp(4τ 2).	9.24. kX (τ) = (1 + sin2τ) exp(3τ2).
9.25. kX (τ) = 6 exp(36τ 2).

ЗАДАНИЕ 10. . Найти корреляционную функцию, дисперсию случайного процесса Z(t), взаимную корреляционную функцию k_XZ (t₁,t₂). В задачах, в которых корреляционная функция k_X (τ) содержит , рассмотреть только случай .

10.1. kX (τ) = 8 cos4τ .	10.2. kX (τ) = 1 + 8exp(2|τ|) .
10.3. kX (τ) = 10/ (1 + 4τ 2).	10.4. kX (τ) = 64/ (1+4|τ|) .
10.5. kX (τ) = 2 + 8cos2τ.	10.6. kX (τ) = 64 (14τ) exp(4|τ|) .
10.7. kX (τ) = cos(τ/2) / 4.	10.8. kX (τ) = 64cos2τ.
10.9. kX (τ) = 32/ (1 + 4τ 2).	10.10. kX (τ) = 200exp(10|τ|) .
10.11. kX (τ) = 2 (1 + τ) exp(|τ|) .	10.12. kX (τ) = 162/ (1 + 10τ 2).
10.13. kX (τ) = 125exp(5|τ|) .	10.14. kX (τ) = 54 (1+ 3|τ|)exp(3|τ|) .
10.15. kX (τ) =32 cos22τ.	10.16. kX (τ) =1 + 27/ (4 + 3|τ|) .
10.17. kX (τ) = 81/ (1 + 3|τ|).	10.18. kX (τ) = 8 (1  2τ) exp(2|τ|).
10.19. kX (τ) =10 (1 + 4exp(|τ|).	10.20. kX (τ) =25(1 + 48exp(4|τ|) ).
10.21. kX (τ) = 216exp(6|τ|).	10.22. kX (τ) = 25 (1+ 5|τ|)exp(5|τ|).
10.23. kX (τ) = 64cos24τ.	10.24. kX (τ) = 20exp(2|τ|).
10.25. kX (τ) = 1 + 16/(1+4|τ|).

ЗАДАНИЕ 11. k_X (τ)  корреляционная функция стационарного случайного процесса X(t). Найти его спектральную плотность.

11.1. kX (τ) = (cosτ+sin|τ|) exp(|τ|).	11.2. kX (τ)= 5(sin2τ)/τ.
11.3. kX (τ) = 4(1+2|τ|) exp(2|τ|).	11.4. kX (τ)= 81exp(9τ2).
11.5. kX (τ) = 16 cos2τ exp(|τ|) .	11.6. kX (τ)= 64exp(4|τ|).
11.7. kX (τ) = 4exp(τ2).	11.8. kX (τ)= 3(cos2τ sinτ)/τ.
11.9. kX (τ) = 3(sin4τ)/ (4τ).	11.10. kX (τ)= 18/(9+τ2)2.
11.11. kX (τ)=	11.12. kX (τ)=
11.13. kX (τ) = 8/(8+2τ2)2 .	11.14. kX (τ)= 32exp(16 τ 2).
11.15. kX (τ) = 27exp(|τ|)cos3τ.	11.16. kX (τ)= 20/(1+25τ 2) .
11.17. kX (τ) = sin24τ / (16τ2).	11.18. kX (τ)= sin22τ / τ2.
11.19. kX (τ) = 16exp(4τ2).	11.20. kX (τ)= 9/(1+9τ2).
11.21. kX (τ) = 4exp(2|τ|).	11.22. kX (τ)= 2exp(|τ|)(1+|τ|).
11.23. kX (τ)=	11.24. kX (τ)=
11.25. kX (τ)= 8exp(2|τ|)cos τ.

ЗАДАНИЕ 12. S_X(ω)  спектральная плотность стационарного случайного процесса X(t). Найти его корреляционную функцию.

12.1. SX (ω)=

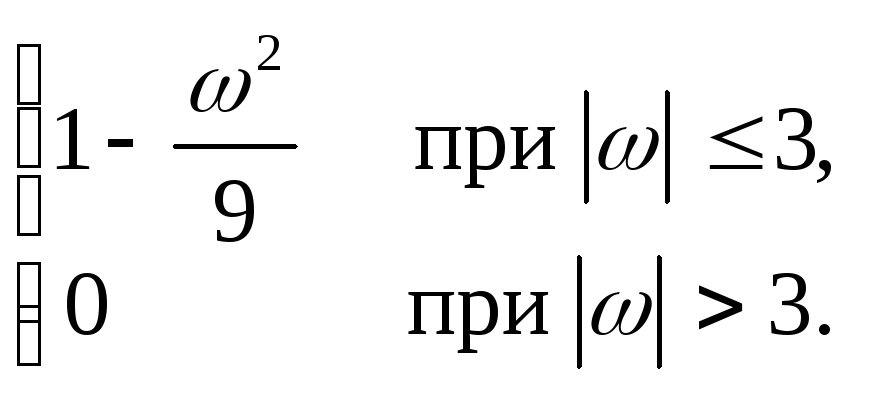
12.2. SX (ω)= 20/(25+ω2).

12.3. SX (ω)=

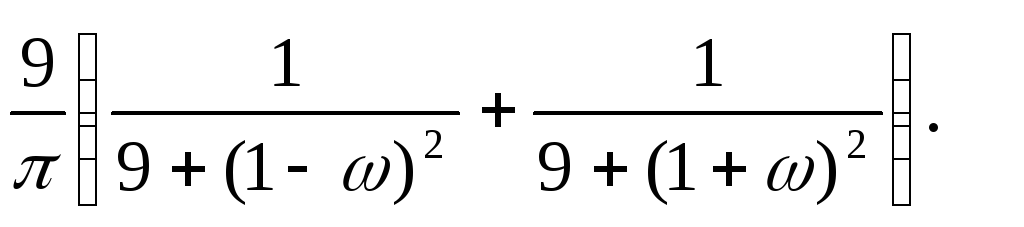
12.4. SX (ω)= 4exp(ω2).

12.5. SX (ω)=

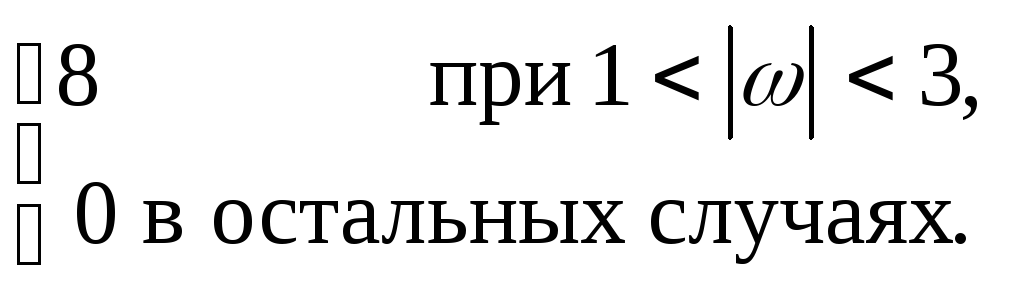
12.6. SX (ω)=

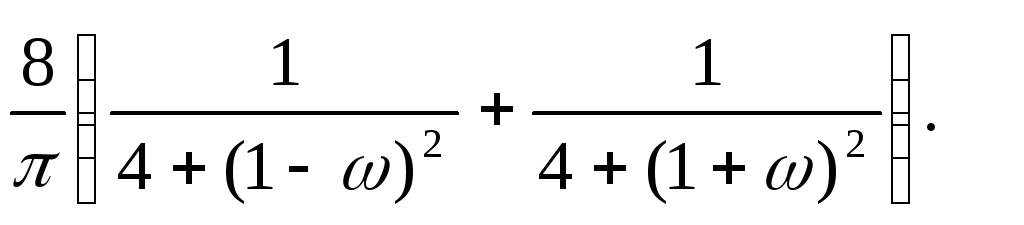
12.7. SX (ω)= exp(|ω|/2).

12.8. SX (ω)= 27exp(ω2/36).

12.9. SX (ω)= 2(sin4ω)/(4ω).

12.10. SX (ω)= 12/(π(9+ω2)).

12.11. SX (ω)= 4/(π(1+ω2)2).

12.12. SX (ω)=

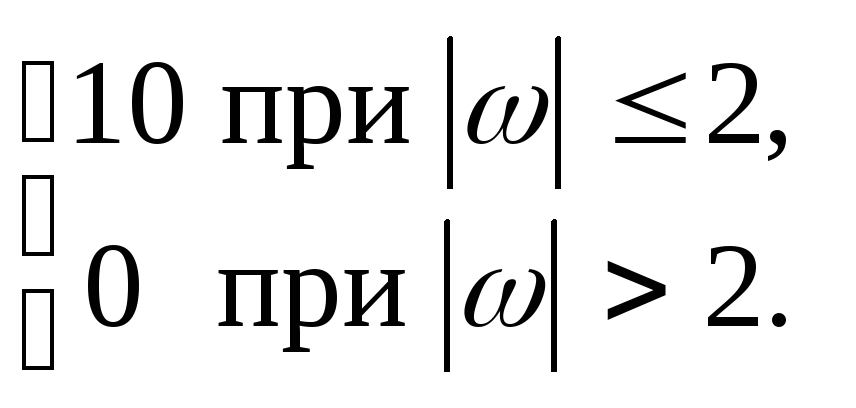
12.13. SX (ω)= 10(sin2ω)/ω2.

12.14. SX (ω)=

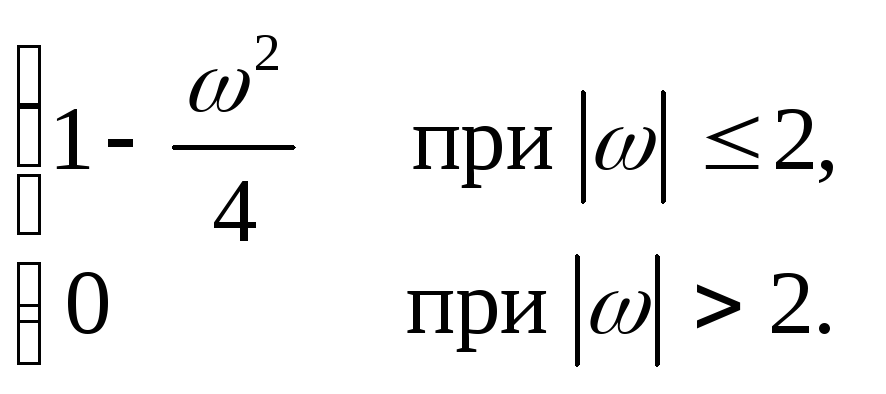
12.15. SX (ω)= 2exp(|ω|/9).

12.16. SX (ω)=

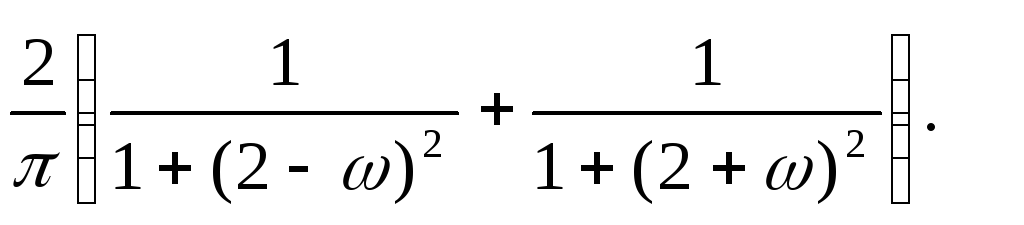
12.17. SX (ω)= 10/(π(4+ω2)).

12.18. SX (ω)=

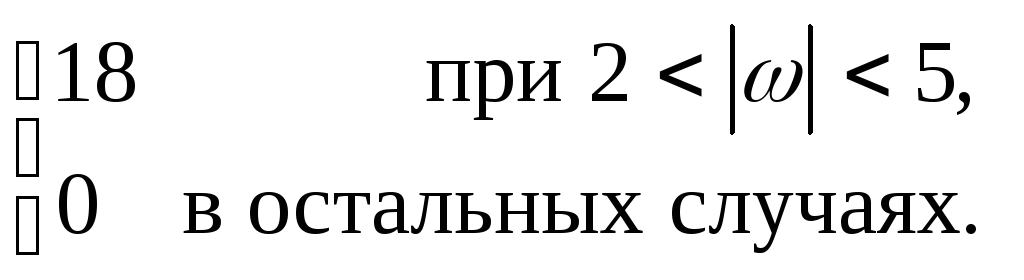
12.19. SX (ω)=

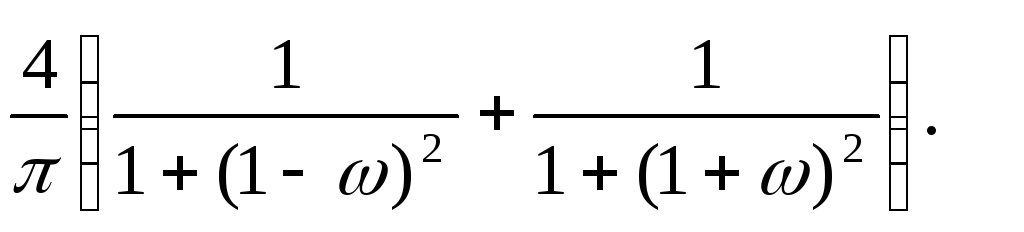
12.20. SX (ω)= 32/(π (4+ω2)2).

12.21. SX (ω)= 6(1cos2ω)/( πω2).

12.22. SX (ω)= 10(sin2ω)/ω.

12.23. SX (ω)= exp(ω2/4).

12.24. SX (ω)= 2exp(|ω|/4).

12.25. SX (ω)=

ЗАДАНИЕ 13. На вход стационарной линейной динамической системы, описываемой данным дифференциальным уравнением, подается стационарный случайный процесс X(t) с математическим ожиданием m_X и спектральной плотностью S_X(ω). Найти математическое ожидание и дисперсию случайного процесса Y(t) на выходе системы в установившемся режиме.

13.1. y+5 y+6 y = 3x, mX = 10, SX (ω)=

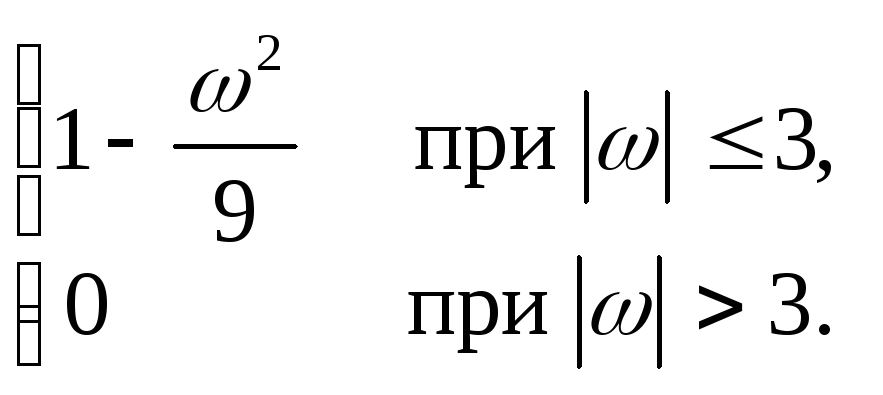
13.2. y+4 y+4 y = 3x, mX = 14, SX (ω)= 2(sin4ω)/ω.

13.3. y+3 y+2 y = x+8x + 15x, mX = 6, SX (ω)= 10/(25+ω2).

13.4. y+4 y+4 y = x, mX = 10, SX (ω)= 6(1cos2ω)/( πω2).

13.5. y+2 y+ y =x + 3x, mX = 4, SX (ω)= 27/(π(9+ω2)2).

13.6. y+10 y+25 y = x, mX = 14, SX (ω)= 10 (sinω)/ω.

13.7. y+ y =2 x, mX = 12, SX (ω)=

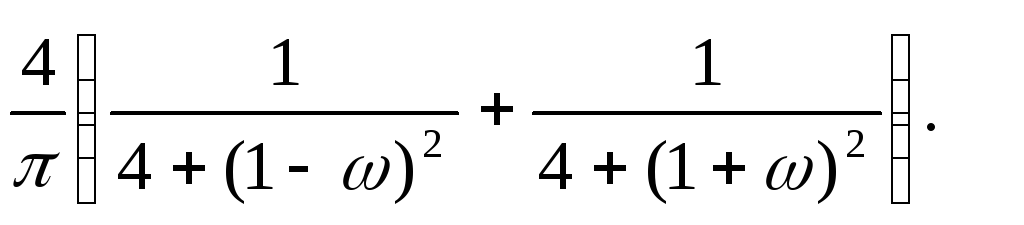
13.8. y+7 y+10 y = x + 4x, mX = 6, SX (ω)= 10/(16+ω2).

13.9. y+4 y+ 3 y = x+8x + 16x , mX = 7, SX (ω)= 32/(π(16+ω2)2).

13.10. y+ 3y = 4x, mX = 18, SX (ω)= (10sin5ω)/ω.

13.11. y+ 5y = x, mX = 20, SX (ω)= (2sin24ω)/ω2.

13.12. y+3 y = x+ x, mX = 5, SX (ω)=

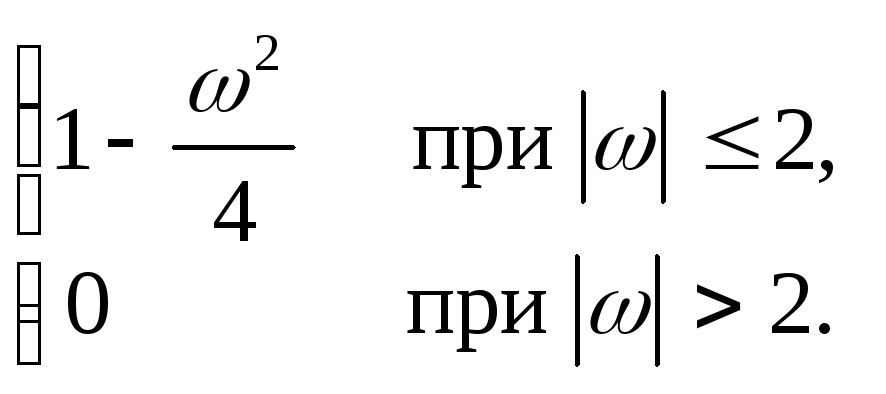
13.13. y+6 y+ 5y = x+ 2x, mX = 15, SX (ω)=

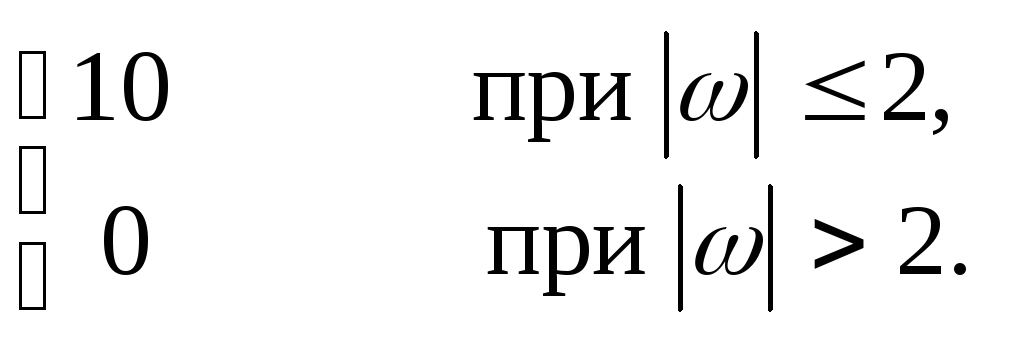
13.14. y+ 4y =2x, mX = 12, SX (ω)=

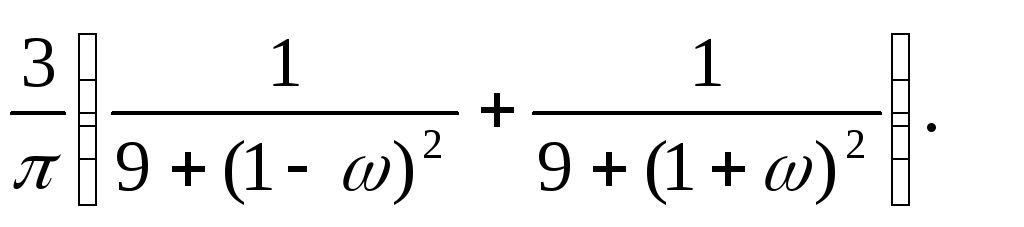
13.15. y+ 5y = 4x, mX = 8, SX (ω)= 4(1cos6ω)/ (πω2).

13.16. y+6 y+ 5y = x, mX = 16, SX (ω)= 10 (sin28ω)/ω2.

13.17. y+3 y = 4x, mX = 12, SX (ω)=

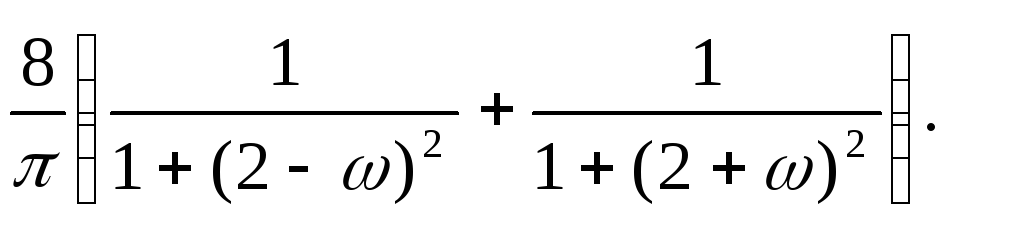
13.18. y+4 y+3 y = x, mX = 16, SX (ω)= (1cos4ω)/ (πω2).

13.19. y+5 y = 4x, mX = 6, SX (ω)= 5/(4+ω2).

13.20. y+2 y = 4x, mX = 6, SX (ω)=

13.21. y+ 4y =10x, mX = 9, SX (ω)= 6/(π(1+ω2)2).

13.22. y+ 2y = x+ 3x, mX = 2, SX (ω)= 6 (sin22ω)/ω2.

13.23. y+4y = 5x, mX = 9, SX (ω)=

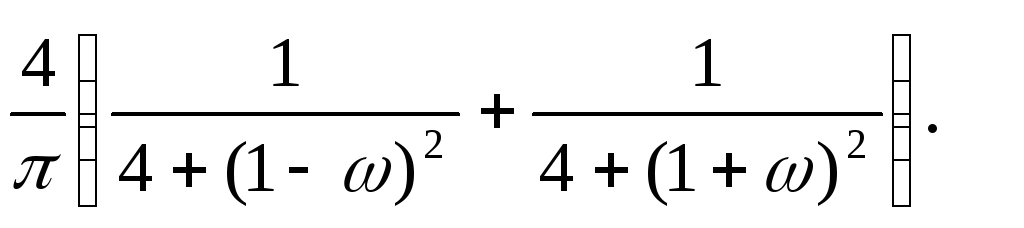
13.24. y+ 3y = 4x, mX = 18, SX (ω)= (10sin5ω)/ω.

13.25. y+4 y = 3x, mX = 5, SX (ω)=

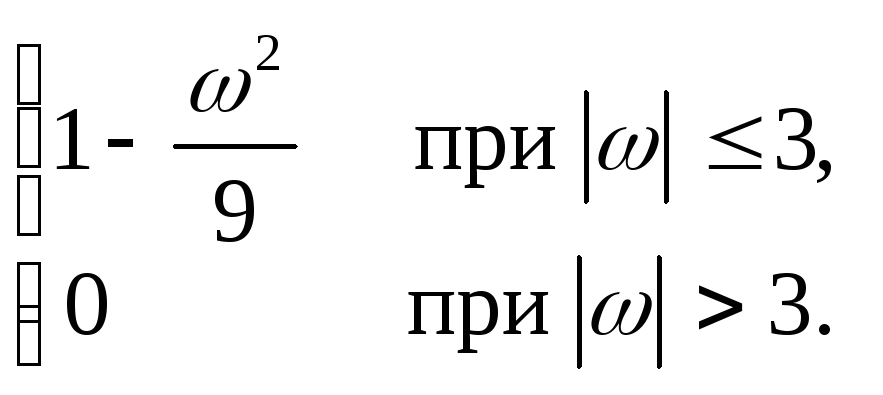
ЗАДАНИЕ 14. На вход стационарной линейной динамической системы, описываемой данным дифференциальным уравнением, подается стационарный случайный процесс X(t) с корреляционной функцией k_X (τ). Найти спектральную плотность S_Y (ω) случайного процесса Y(t) на выходе системы в установившемся режиме.

14.1. y+6 y+ 5y = x+ 7x+ 10x, kX (τ)= 18/(9+τ2)2.

14.2. y+6 y+ 9y = x+ 2x, kX (τ)=

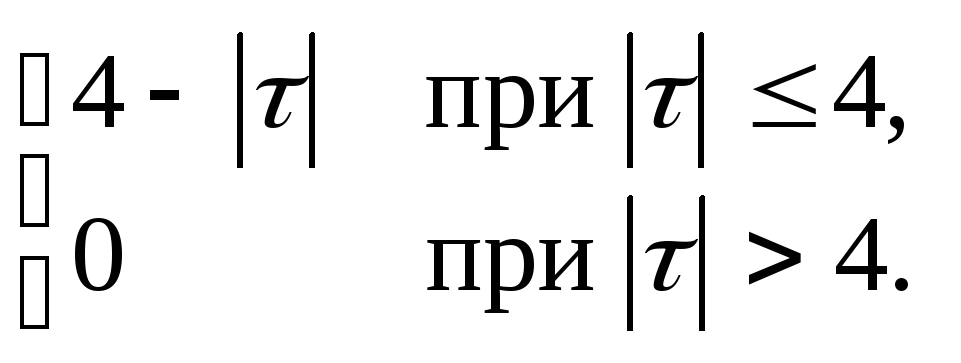
14.3. y+3 y+ 2y = x+ 10x+ 25x, kX (τ)= 20/(1+25τ 2).

14.4. y+5 y+ 6y = x, kX (τ)=

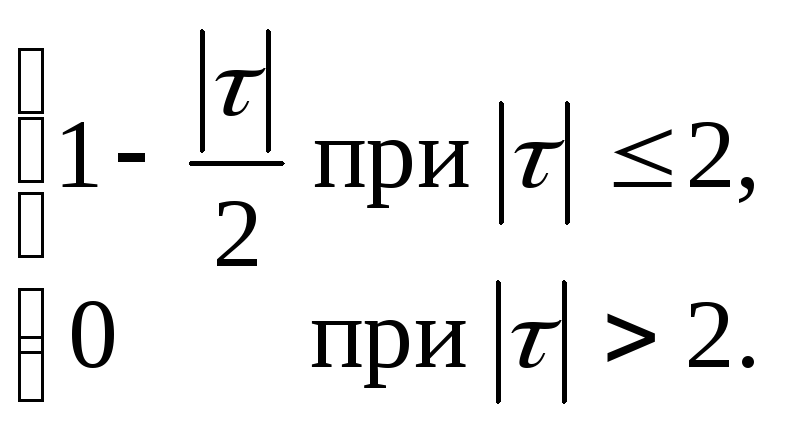
14.5. y+5 y+ 4y = 2x, kX (τ)= exp(|τ|)(cosτ+sin|τ|).

14.6. y+4 y+ 3y = x+ 2x, kX (τ)= 4exp(2|τ|)(1+2|τ|).

14.7. y+7 y+ 6y = 5x, kX (τ)= 16exp(|τ|)cos2τ.

14.8. y+7 y+ 10y = x+ 5x+ 4x, kX (τ)= 4exp(τ2).

14.9. y+7 y+ 12y = x+ 4x+ 4x, kX (τ)= 3(sin4τ)/(4τ).

14.10. y+4 y+ 4y = x+ 7x, kX (τ)=

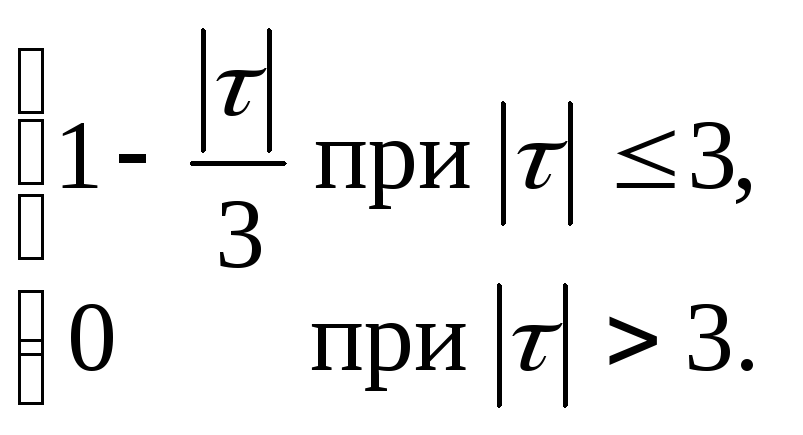
14.11. y+6 y+ 8y = x, kX (τ)= 8/(8+2τ2)2 .

14.12. y+8 y+ 7y = 2x, kX (τ)= 27exp(|τ|)cos3τ.

14.13. y+8 y+ 12y = 5x, kX (τ)=

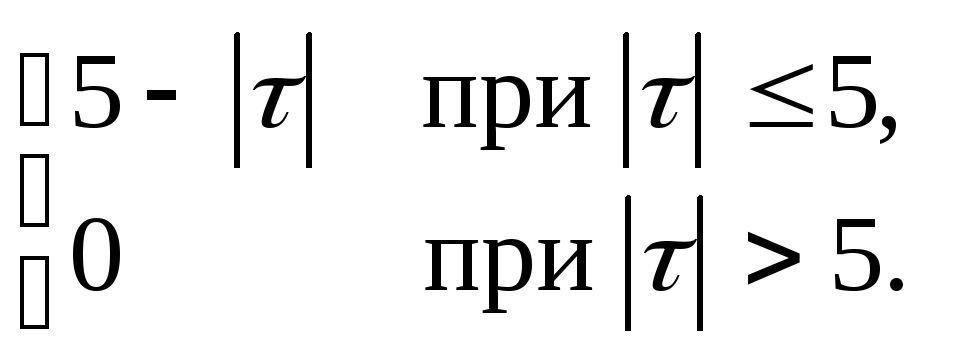
14.14. y+8 y+ 16y = x+ 2x, kX (τ)= 16exp(4τ2).

14.15. y+8 y+ 15y = x+ x, kX (τ)= 8/ (1+16τ2).

14.16. y+10 y+ 25y = x+ 3x, kX (τ)= 8exp(2|τ|)cos τ.

14.17. y+10 y+ 9y = x+ x, kX (τ)= 4exp(2|τ|).

14.18. y+10 y+ 16y = x+ 2x, kX (τ)= 5(sin2τ)/τ.

14.19. y+10 y+ 21y = x+ 3x, kX (τ)= 2exp(|τ|)(1+|τ|).

14.20. y+10 y+ 24y = x+ 6x, kX (τ)= 3(cos2τ sinτ)/τ.

14.21. y+9 y+ 8y = x+ 8x, kX (τ)= 64exp(4|τ|).

14.22. y+9 y+ 14y = x+ 7x, kX (τ)= 32exp(16 τ 2).

14.23. y+9 y+ 18y = x+ 3x, kX (τ)=exp(|τ|)(cos2τ+0.5sin2|τ|).

14.24. y+9 y+ 20y = x+ 10x, kX (τ)= 81exp(9τ2).

14.25. y+12 y+ 36y = x+ 6x, kX (τ)= 9/ (1+9τ2).

ЗАДАНИЕ 15. На вход стационарной линейной динамической системы, описываемой данным дифференциальным уравнением, подается стационарный случайный процесс X(t) со спектральной плотностью S_X(ω). Найти корреляционную функцию k_Y (τ) случайного процесса Y(t) на выходе системы в установившемся режиме.

15.1. y+12 y+ 36y = x, SX (ω) = 10(sin8ω)/ (πω).

15.2. y+ y = x, SX (ω)=

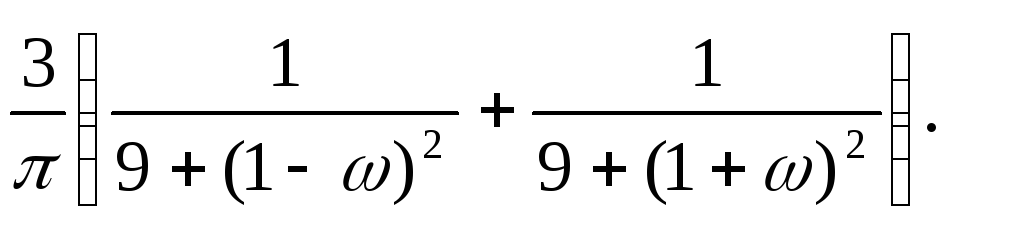
15.3. y+4 y+ 3y = x+2x , SX (ω)= 10/(π(4+ω2)).

15.4. y+5 y+6y = x+2x+x , SX (ω)= 2/(π(1+ω2)2).

15.5. y+ 4y = 5x, SX (ω) =

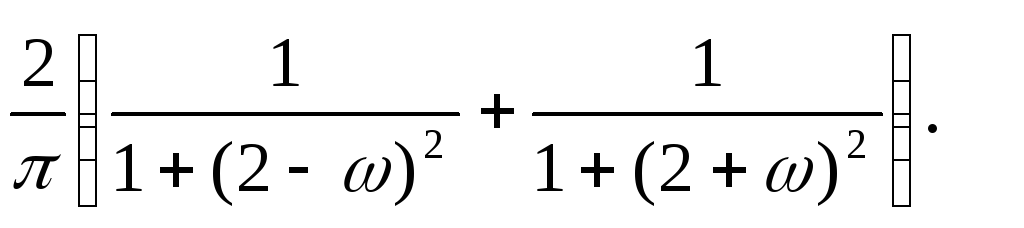
15.6. y+4 y+ 3y = x, SX (ω) = 10(sin2ω)/ (πω).

15.7. y+3 y+2 y = x, SX (ω)= 6 (1cos2ω)/(πω2).

15.8. y+ y = 4x , SX (ω)=

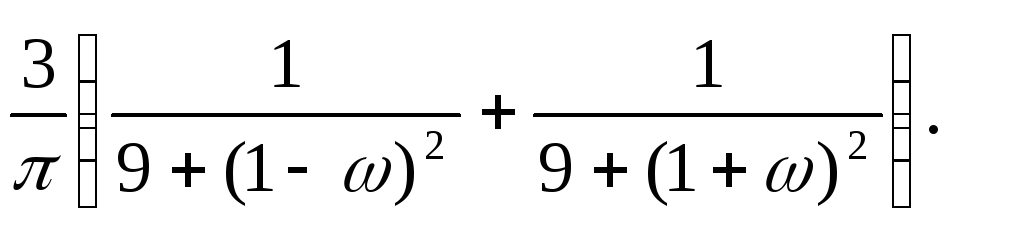
15.9. y+4 y+3y = x+ 2x , SX (ω)= 16/(π(4+ω2)2).

15.10. y+ 3y = 2x, SX (ω) =

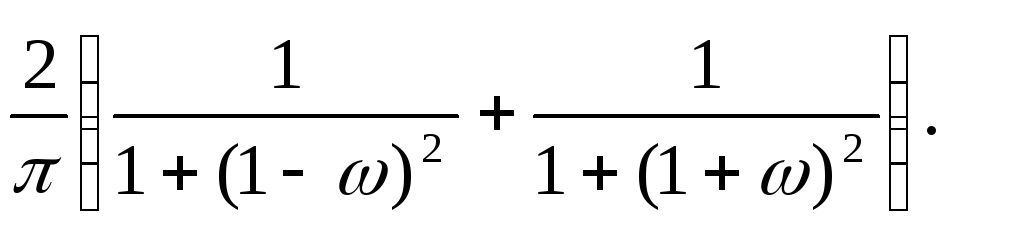
15.11. y+4 y+ 4y = x+3x , SX (ω)= 8/ (π(9 +ω2)).

15.12. y+4 y = 3x, SX (ω)= 3 (1cos6ω)/ (πω2).

15.13. y+ y = x, SX (ω) =

15.14. y+3 y+ 2y = 3x , SX (ω)= 6/ (π(1 +ω2)).

15.15. y+2 y+ y = x+3x , SX (ω)= 27/(π(9+ω2)2).

15.16. y+ 3y = x+2x , SX (ω) = (sin4ω)/ (πω).

15.17. y+ 2y = 3x, SX (ω)= 6/ (π (1+ω2)).

15.18. y+ y = 4x , SX (ω)=

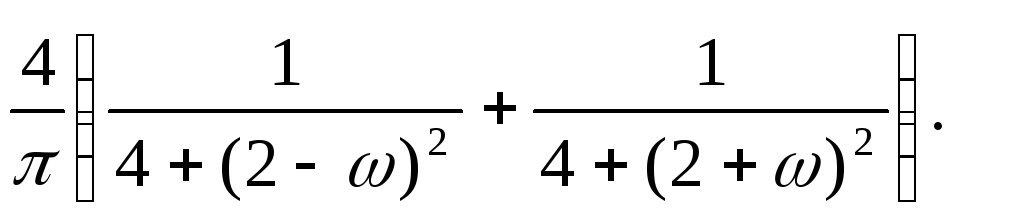
15.19. y+ 2y = 5x, SX (ω) = 9(sin3ω)/ (πω).

15.20. y+ 4y = x+3x , SX (ω)= 8/ (π(16 +ω2)).

15.21. y+2 y = 3x, SX (ω) = (1cos8ω)/(πω2).

15.22. y+ y = 4x , SX (ω)= 54/(π(9+ω2)2).

15.23. y+2 y+ y = 3x, SX (ω) = 8(sin4ω)/ (πω).

15.24. y+ 2y = 3x, SX (ω) =

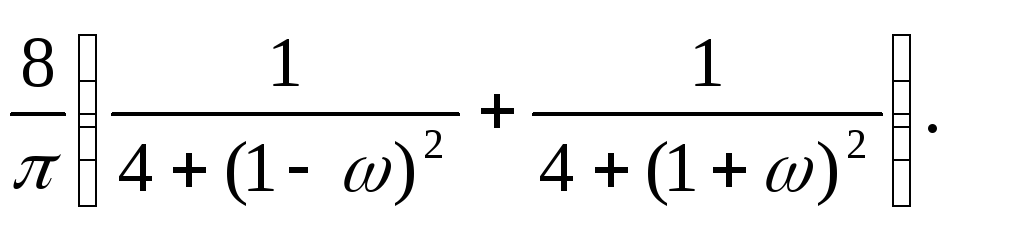
15.25. y+3 y+ 2y = 3x, SX (ω) = 4(sin2ω)/ (πω).