1. Классическое и геометрическое определение вероятности. Примеры. Вложение этих определений в аксиоматику Колмогорова.

(1) Частотное определение вероятности. Возмем симметричную монету и подсчитаем частоту выпадения решки.

^m/_np-частота

m– число выпадений решки,n– число испытаний.

повторяем много раз и считаем частоту, то вероятность будетp.

Частота приближается к вероятности.

Это определение историческое.

(2) Классическое определение вероятности.

Пусть существует n– конечное число одинаковых элементарных исходов и пусть с этим опытом связано событие А, которому соответсвуетmизnэлементарных исходов, тогда за вероятность события А: принимаютp(A)=^m/_n

Пример:

Пусть бросается монета 1 раз.

Исходы: орел, решка.

P(Орла)=¹/₂ ,P(Решки)=¹/₂

Пусть бросают монету два раза

Исходы: орел – 0 00, 01, 10, 11

решка –1

p(исхода)=¼

Найти вероятность того, что сумма была четная (00, 11) p=½

p(A_m) – бросаем монетуmраз

A_m– событие, что выпалоmединиц.

Минусы этого определения:

1. Оно требует симметрию (наличие равновероятных исходов). Это достаточно сложно.

2. Наличие конечного числа событий.

3. Дискретное вероятностное пространство

Пусть существует конечное или счетное множество элементарных событий и для каждого события определяется вероятностиp_iдля каждого элементарного события.

(,p_i,i=1,2…) – эта пара определяет вероятностное пространство.

p_i=p(_i)_i

Событие – множество элементарных событий – А, тогда p(A)=p(_i)

Дискретное определение включает классическое определение p_i=1/n1<i<mp(A)=^m/_n

Минусы:

1) Не всегда известны p_i

2) Оно не всегда всеобщее (бывает не счетное множество)

(4) Существует геометрическая вероятность.

Пусть есть задача, так что удается описать множеством точек в пространстве или на прямой. Каждому событию Асопоставить подмножество точек в множестве точек

 площади

Задача о встрече.

Молодой человек и девушка договорились встретиться в 12ч. Каждый может придти от 12 до 13 ч. Договорились ждать 20 минут. Какова вероятность, что они встретятся.

|x-y|<¹/₃

Эту площадь надо сосчитать

1-⁴/₉=⁵/₉

2. Парадоксы Бертрана их объяснение

Пусть существует круг, в котором выбирается хорда случайным образом, требуется найти вероятность, чтобы длина хорды была > стороны вписанного равностороннего треугольника.

З решения задачи дают разные ответы.

1 решение:

Т.к. круг симметричная фигура, следовательно, можно рассмотреть хорду перпендикулярную диаметру, каждая такая хорда определяется точкой на диаметре.

Поэтому - диаметр. Длиной 2R.

Рассмотрим точки хорд.

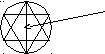
В этих точках длина хорды будет > стороны треугольника.

Это будет 2 радиуса вписанной окружности 2r.

R=2r

P(A)=r/R=½

2 решение:

Т.к. круг симметричная фигура следовательно можно рассмотреть такие хорды один из концов которых находится в одной точке, проведем к ней касательную. - это угол между хордой и касательной.

Нас устраивают только те хорды, которые лежат внутри

треугольника.

P(A)=⁶⁰/₁₈₀=¹/₃

3 решение:

Каждая хорда определяется координатой середины поэтому в качестве - исходный круг.

Т.е. хорды, которые лежат внутри окружности, вписанной в круг.

P(A)=¹/₄

Если пользоваться геометрической вероятностью, то результат может быть неверным.

3. Аксиоматика Колмогорова.

1) Основой является вероятностное пространство. (,F,P)

 - некое множество произвольной формы, множество элементарных событий.

В качестве событий рассматривается подмножество множества :A<, но рассматриваются не все подмножества, а только какая-то совокупность их.

F– совокупность всех событий. Требуется, чтобы:

F– было бы- алгеброй т.е.

1. Если А является событием АF, то и дополнениетоже является событием

2. F

3. Если есть последовательность событий. А₁, А₂, … А_nF, то их объединение тожеF

При этих условиях на множестве всех событий задаем функцию P(A),AF, она обладает свойствами:

1. P(A) – неотрицательной (P(A)>=0)

2. P() =1

3. Если есть последовательность событий, которые попарно не пересекаются.

A₁,A₂,…A_nA_j=0, то P(A_i)=P(A_i).

Тогда эта тройка называется вероятностным пространством.

Действия над событиями.

1) AВ (сумма событий)

А+В – это событие которое заключается в том, что произошло событие А или В или они произошли одновременно.

2) АВ=АВ (произведение событий)

Состоит в том, что эти события произошли одновременно.

3) Дополнение события А, состоит в том, что событие А не произошло.

4) АB(А входит в В): если произошло событие А, то произошло и В.

5) А₁,…,A_n– набор событий,A=A_i–A произошло, если хотя бы одно изA_i произошло.

Основные свойства вероятности.

1. Пустое множество 0FиP(0)=0 т.к.F, а пустое множество можно рассматривать как дополнение.

00=0

P(0P(0)P(

2. Если AВ, тогдаP(A)<P(B)

Доказательство:

В=(В\А)А, (В\А) и А не пересекаются, тогдаP(В)=P(В\А)+P(А)>P(A) т.к.P>0

3. Вероятность любого события 0<P(A)<1

Ap(A) <1 т.к.p()=1, подставим во второе свойство вместоB-.

4. Условная вероятность. Независимость событий. Примеры.

Условная вероятность:

Хотим определить А при условии, что произошло событие В.

P(B)0

Пусть есть и есть события В и А

И мы узнали, что В произошло, у нас изменилось вероятностное пространство, теперь рассмотрим В, оно играет роль . Рассмотрим не А, а пересечение А с В.

Мера вероятности A– вероятность произведенияAB, но надо нормировать поB.

Теорема умножения вероятностей:

Р(AB)=P(A/B)P(B)

Пример:Вероятность рождения девочки и вероятность рождения мальчика ½. Рассмотрим семьи с двумя детьми. Известно, что в некоторой семье один мальчик, найти вероятность того, что второй ребенок, тоже мальчик.

мммддмдд

P=¼ ¼ ¼ ¼

Нас устраивает, когда в семье есть 1 мальчик, тогда нас устраивают подчеркнутые сочетания.

Переходим в другое вероятностное пространство, у нас три события, => вероятность второго мальчика составляет ¹/₃

P(м м/один м)=^¼/_¾=¹/₃

Обобщим теорему вероятностей:

P(ABC)=P(A/BC)P(BC)=P(A/BC)P(B/C)P(C)

Независимость событий:

Событие Aне зависит от В, если

P(A/B)=P(A) (вероятность А не изменяется), значит

P(AB)=P(A)P(B),P(B)0

Если бы мы рассматривали независимо В от А, то мы бы получили, что P(AB)=P(A)P(B), Р(А)0, но событие вероятности 0 не зависит от другого события =>

P(AB)=P(A)P(B) – определение независимости 2-х событий.

Пример:1) Пусть существуют 36 карт. А – мы выбираем туза, В – мы выбираем красную карту.

А и В независимы.

Р(А)=⁴/₃₆=¹/₉

P(B)=½

P(AB)=²/₃₆=¹/₁₈– вероятность выбрать красного туза

P(AB)=P(A)P(B)

Пусть колода не полна, т.е. одну карту отбросили, то независимость нарушается.

Определение:

А₁, А₂, … А_nнезависимые события, если:

1. P(A_iA_j)=P(A_i)P(A_j)ij

2. P(A_iA_jA_k)=P(A_i)P(A_j)P(A_k)ijk

3. …

Должно выполнять при всех наборах из последовательности А_i.

1. Попарная независимость.

2. Взаимная независимость событий.

Пример:Тетраэдр, у него одна сторона красная, другая черная, третья белая, а четвертая во все цвета.

A – красный P(A)=P(B)=P(C)=½

B– черный

С – белый P(AB)=P(AC)=P(BC)=¼

P(ABC)=¼

Взаимной независимости нет, хотя попарная есть.

5. Формулы полной вероятности и Байеса. Интерпретация формулы Байеса.

Формула полной вероятности:

Пусть существуют события H₁,H₂, …H_nи событие А, которое обладает сойствами.

1. H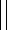_iH_j=0, H_i – рассекает А

2. A<_iH_i

Набор клеточек иллюстрирует нашу ситуацию.

Формула полной вероятности:

P(A)=ⁿ_i=1P(A/H_i)P(H_i)

Если H– это квадрат, тоP(H_i) – это разбиение квадрата,H_i=- набор событий образует полную группу событий.

Доказательство:

Пример:

Пусть существует 3 завода, которые выпускают телевизоры одной марки.

Завод	1	2	3
Доля продукции	¼	¼	½
Процент брака	1	2	3

Какова вероятность бракованного телевизора?

Н_i– событие, что купили телевизор наi-том заводе.

P(A/H₁)=0,01

P(A/H₂)=0,02

P(A/H₃)=0,03

P(A)=0,01¼ +0,02¼+0,03½ =0,0225

Пример:Существует 28 костей, должны выбрать 2 кости, какова вероятность того, что их можно составить.

H₁– первая кость есть дупль.

H₂=H₁

P(H₁)=⁷/₂₈=¼

P(H₂)=¾

P(A\H₁)=⁶/₂₇

P(A\H₂)=¹²/₂₇

P(A)=¼⁶/₂₇+¾¹²/₂₇=⁴²/₁₀₈=⁷/₁₈

Формула Байеса:

Пусть существует полная группа событий с известными вероятностями: H₁,H₂,…H_n.

P(H_i) – априорные вероятности.

Потом происходит эксперимент и наблюдается событие А.

А P(H_i/A) – апостериорные вероятности.

Как из априорной получить апостериорную.

- формула Байеса.

Пример:

Купили телевизор и он бракованный, определить вероятность, на каком заводе произведен.

P(H₂/A)=²/₉

P(H₃/A)=²/₃

6. Задача о рассеянной секретарше. Формула Сложения вероятностей.

Теорема сложения вероятностей.

Пусть существует 2 произвольных события А и В, то

P(AВ)=P(A)+P(B)-P(AB) (4)

Доказательство:

P(A)=P(A\B)+P(AB) (1)

P(B)=P(B\A)+P(AB) (2)

P(AВ)=P(A\B)+P(B\A)+P(AB) (3)

Т.к. все 3 множества не пересекаются, то подставим в (3) (1) и (2), и получим (4)

Следствие 1:

P(AВ)<P(A)+P(B), т.к.p>0 и в (4) мы вычитаем, по индукции оно распространяется на любое число событий.

P(A_i)<P(A_i)

Теорема может быть распространена на любое количество событий.

Следствие 2:

Пусть существует A₁,A₂, …A_n– события, тогда

P(ⁿ₁A_i)=ⁿ_i=1P(A_i)-ⁿ_ijP(A_iA_j)+ⁿ_ijkP(A_iA_jA_k)+…+(-1)ⁿ⁺¹P(A₁A₂_…A_n)

Можно доказать методом математической индукции.

Докажем для случая трех слагаемых:

P(A₁A₂A₃)=P(A₁А₂)+P(A₃)-P((A₁А₂)A₃)=P(A₁)+P(А₂)+P(A₃)-P(A₁A₂)-P(A₁A₃)-P(A₂A₃)+ P(A₁A₂A₃)

Непрерывность вероятностей

Счетное объединение событий – событие и пересечение событий есть событие. Для этого покажем, что

А F=>АF– пересечение множеств изFесть множество изF

5а) Пусть существует возрастающая последовательность событий, т.е. для любого nA_n<A_n+1

A_n– возрастающая последовательность.

И пусть A=A_n=>P(A)=lim_n->P(A_n)

5б) Пусть существует убывающая последовательность событий, т.е. для любого nB_n>B_n+1

_n– убывающая последовательность.

И пусть B=_n=>P(B)=lim_n->P(B_n)

Покажем, что 5aсходиться к 5б

Пусть 5a- справедливо, тогда 1-P(A)=lim_n->(1-P(A_n)),P(A)=lim_n->P(A_n)

=A_n(по формуле де Моргана)

тогда P(A_n)=lim_n->P(A_n), т.к.A_n– произвольно иA_nвозрастает, тоA_nубывает

В_n=A_nи получимP(B_n)=lim_n->P(B_n)

Поэтому достаточно доказать только одно 5aили 5б.

Доказательство:5а

Представим А как:

А=А₁(А₂\A₁)(А₃\A₂)… (А_n+1\A_n)

Все эти слагаемые не пересекаются.

P(A)=P(A₁)+P(А₂\A₁)+…+P(А_n+1\A_n)

Пусть А₀– пустое множество

P(A)=

7. Схема Бернулли, полиномиальная схема. Примеры.

Бросается монета nраз, и интересуются количеством выпадения герба -p, и выпадения решки –q.

n– независимых испытаний с двумя исходами. В любом испытании эти исходы называются успехом – У, другой неудачей – Н.

Р(У)=р

P(H)=q=1-p

Независимые испытания У₁, У₂, … У_n

У – 1, H– 0 => Элементарные исходы

Результат: Последовательность из 0 и 1. =(₁,…,_n)

P()=p^mq^n-m,

где m– количество 1;n-m– количество 0.

Надо, чтобы сумма таких вероятностей равнялась 1:

_P()=

P_n(m)=C_n^mp^mq^n-m– формула Бернулли (mуспехов изnиспытаний).

Смысл C_n^m: сколькими способами можно разбить группу изnэлементов на 2 подгруппы изmиn-mэлементов.

В качестве примера – бросание монеты (необязательно симметричной)

Определить, в каком случае эта функция возрастает, а в каком убывает?

Для этого - возрастает

Т.е.

np-mp>mq+q

np>m(p+q)+q

np>m+q

m<np-1+p=(n+1)p-1

до тех пор пока m<(n+1)p-1 – функция возрастает, иначе убывает.

Если рисовать график этого соотношения, то

P_n(m)

^{1 2 3 n}

Даже в точке максимума p_n(m)0, т.к. график растянутый.

Пример: блуждание по прямой.

Пусть существует прямая линия, на которой целые числа. Пусть некий подвыпивший человек блуждает в округе точке 0. С вероятностью ½ - влево или вправо. Какова вероятность, что он вернется в точку 0, через nшагов.

У – шаг вправо

Н – шаг влево

Чтобы он вернулся У=Н т.е. nдолжно быть четным числом.

N=2k;p=q=½ всего испытаний 2kи былоkуспехов.

P_2k(k)=C_2k^k/2^2k

Схема Бернулли ограничена:

Если мы бросаем игральную кость у нас 6 вариантов, а не 2 исхода.

Когда количество не 2, а k.

Пусть существует n– независимых испытаний сkисходами, вероятности каждого исхода:p₁,p₂,…,p_k;^k_i=1p_i=1.

Будем интересоваться P_n(n₁,n₂,…,n_k), гдеn₁+n₂+…+n_k=nвероятность того, что в результатеnиспытаний появятсяn₁исходов первого типа,n₂– исходов второго типа и т.д.n_k

Она вычисляется:

P_n(n₁,n₂,…,n_k)=C_n^n1,n2…*p₁ⁿ¹*…*p_k^nk

С_n^n1…nk=n!/n₁!n₂!… приn=2 получается формула Бернулли

Смысл С_n^n1…nk: сколькими способами множество изnэлементов можно разбить наkчастей, т.о., чтобы в первой группе былоn₁элементов, во второйn₂элементов, вk–n_k.

Биномиальная схема – Бернулли

Полиномиальная схема – для k>2.

Пример:

Блуждание по плоскости.

Пусть имеется на плоскости целочисленные точки.

Некоторая частица путешествует по ним. Она сдвигается в различных направлениях (С,Ю,З,В) cравной вероятностьюp=¼ .Cкакой веростностью частица вернется в исходную точку.

Она должна вернуться по х и по у. Т.е. С=Ю, З=В. n– четное число=2k

= (C_2k^k/2^2k)²- можно вычислить это выражение следующим образом:

Повернем оси координат на 45^ои будем рассматривать проекции координат частицы на новые оси, тут шаг будет¹/₂. Чтобы частица вернулась, надо чтобы она вернулась и по проекциям.

Вероятность попадания в точку Х = ¼ т.е. проекция тоже блуждает по осям. Вероятность сдвинуться вправо или вверх равна произведению вероятностей, т.е. они независимы. Тогда вероятность возвращения в начало координат.

P(A)=(C_2k^k/2^2k)²

8. Теорема Пуассона.

Пусть мы имеем не 1 испытание Бернулли, а серию испытаний Бернулли. Первая серия состоит из 1 испытания – вероятность успеха p₁, вторая серия из 2-х –p₂,…

И пусть р зависит от n.

E₁₁ p₁

E₁₂ E₂₂ p₂

E_1n E_2n … E_2n p_n

np=(либо стремится, либо равно), тогда

|P_n(m)|0 (n∞)

т.е. в качестве приближенного значения можно взять.

Серия схем Бернулли берется для того, чтобы pне было постоянным. Вероятность успеха очень мала, поэтому называют законом редких событий.

Доказательство:

P_n(m)=C_n^mP^mq^n-m=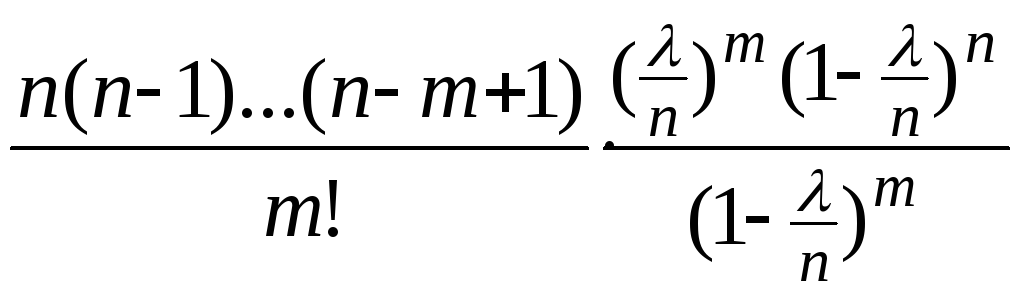

При доказательстве будет, для простоты, считать np=,m– фиксированное.

Т.к. n=>n0, поэтому знаменатель1

- эта формула получается когдаp– мало, а количество успеховm– фиксировано.

9. Локальная и интегральная теорема Муавра Лапласа.

1. Локальная теорема Муавра-Лапласа

Рассматривается величина x=x_m,n(зависит отmиn).

p– фиксированное число и не зависит отmиn,mиnменяются таким образом, чтобыx_n,mбыла ограничена |x_n,m|<C. В этом случае справедливо соотношение.

Это означает, что в качестве приближения для P_n(m) надо брать знаменатель этого выражения.

P должно быть маленьким, n – большим.

Когда практически применяется 1 и 2 теорема – это зависит от p_n(m). 1 – когдаnpне превосходит 4-х чисел, а вторая когда превосходит 5.

Доказательство:

Формула Стирлинга: n! =nⁿe^-2n(1+0(1))

Если мы перенесем знаменатель в числитель, то сравним.

будем применять формулу Стирлинга кm,nиn-mнадо доказать, чтоn-m,m.

Представим m-np=xnpq

1. m=np+xnpq, т.кp,q– фиксированы, х – ограничена,n

2. n-m=nq-xnpq, т.кp,q– фиксированы, х – ограничена,n

Т.е. мы применяем формулу Стирлинга к mиn-m

Рассмотрим выражение:

все что касается n, перенесем в знаменатель. Разделим все наn^m

учитывая (1) и (2) получим:

возьмемln:

ln()=по формуле Тейлора разложимln:

==

==

т.е. получим, что выражение ~ч.т.д.

2) Интегральная теорема Муавра-Лапласа

x=

n,p,q– фиксированные числа.

Тогда

P(<x)Ф(х) – функция Лапласа

Ф(х)= - значение функции в специальной таблице.

Интегральная теорема Муавра-Лапласа применяется тогда, когда мы можем интегрировать вероятность того, что вероятность находится в интеграле.

P(a<m<b). Поэтому мы можем легко свести ее к интегральной теореме Муавра-Лапласа.

P(a<m<b)=

Чтобы найти подобную вероятность, надо подсчитать величины.

ии по таблице определить значение вероятности.

10. Случайные величины их распределения. Свойства функции распределения.

Вероятностное пространство: (,F,P)

Случайная величина:

X=X(),- измеримая на.X- случайная величина, она зависит от случая.

F– Сигма-алгебра событий.B– Сигма-алгебра Борелевских множеств, которая индуцирована интервалами. Рассматриваются интервалы и рассматривается сигма-алгебра в которую входят все интервалы.

Измеримость – X^-1(B)F,BВ

Чтобы мы могли это вычислить P(XВ)=P(X^-1(B)) т.к. вероятность задана наF.

Способы описания случайных величин.

q(B)=P(XB)=P(X^-1(B)) – она задает какую-то меру на вещественной прямой.

q(B) – вероятностная мера.

Если B₁B₂=0, тогдаq(B₁B₂)=q(B₁)+q(B₂)

q(B₁B₂)=P(XB₁B₂)=P(X^-1(B₁B₂))=P(X^-1(B₁)X^-1(B₂))=P(X^-1(B₁))+P(X^-1(B₂))= =P(XB₁)+P(XB₂)=q(B₁)+q(B₂)

q(B) – называется распределением случайной величины, т.е. при отображенииXв вещественную прямую получаем распределение.

Т.к. распределение достаточно сложно, то вводят другие величины.

Функция распределения случайной величины:

F(x)=P(X<x)=q((-,x)), вероятность того, что случайная величина <xили распределение от -до х.

Функция распределения однозначно определяет q, т.к.

q([a,b))=q((-,b))-q((-,a))

q((-,b))=q((-,a))+q([a,b)) – эти два множества не пересекаются.

Это означает, что если P(X[a,b))=F(b)-F(a), мы может найтиqот объединения интервалов, т.е.F(x) однозначно определяетq.

Свойства функции распределения:

1. 0<F(x)<1

2. F(x) – не убывает – это следует изP(X[a,b))=F(b)-F(a), т.е. еслиb>a, тоF(b)>F(a), т.к.F(b)=F(a)+P(X[a,b))>F(a),P(X[a,b))>0.

3. 

Доказательство:

Достаточно доказать, что для любой последовательностиx_n

Пусть такая последовательность задана (возрастающая), введем события А_nтакие что А_n={:X(<x_n}.

A_n– возрастает, каждое следующее событие содержит предыдущее.

Обозначим А=_nA_n={:}=- это есть множество всех, поэтому P(A)=1, тогдаP(A_n)1 приn=>F(X_n)1.

4. 

Доказательство:

Доказать, что

Точно такое же, но используется вторая формулировка непрерывности вероятности.

Пусть задана убывающая последовательность: x_n-, введем события А_nтакие что А_n={:X(>x_n}.A_n– убывает.

Обозначим А=_nA_n все А_n происходят одновременно, поэтому А=_nA_n=0 P(A)=0, тогдаP(A_n)0приn=>F(X_n)0.

5. Функция распределения непрерывна слева.

F(x) – непрерывна слева, т.е.xвозрастает и сходится кx₀, тогдаFбудет сходитьсяF(x₀):

F(x)F(x₀).

Введем те же самые А_nи предположим, чтоx_nx₀.A=_nA_n– формула непрерывности вероятности, тогдаP(A_n)P(A) =>F(x_n)F(x)

A_n={x<x_n},ax_nx₀, тогдаA={:nx()<x_n}={:X(x}, поэтомуP(A)=F(x).

Замечание:

1. Эти 5 свойств – это есть полный набор свойств F(x) в том смысле, что еслифункцияF, которая удовлетворяет этим 5 свойствам, то можно найти такую случайную величину, для которой эта функция будет функцией распределения. Т.о. если нужно узнать является лиFфункцией распределения, достаточно проверить эти 5 свойств, и если хотя бы одно свойство нарушается, тоFне является функцией распределения.

2. Принимается такое определение функции распределения: F(x)=P(X<x) – при таком определении все свойства сохраняются, кроме 5, оно заменяется на свойство о непрерывности справа.

11. Свойства одномерных и многомерных плотностей распределения.

Одномерные плотности распределения:

1) Мы говорим, что случайная величина Xотносится к дискретному типу (или имеет дискретное распределение), если она принимает конечное или счетное число значений. Это означает, что существует такой набор цифрx₁,x₂, …,x_n. т.ч..

В этом случае, если значение Xзанумеровать, то мы может расписать характеристикуp_k=P(X=x_k). Набор однозначно определяет распределение. Можно задать таблицу.

x1	x2	…	xn
p1	p2	…	pn

Эта таблица означает, что мы задаем функцию p(x), гдеxравно одному изx_n.

Условно назовем p(x) – дискретной плотностью распределения.

F(x)=P(X<x)=_xi<xP(x=x_i)=_xi<xp(x_i).

С другой стороны p(x_i) – это скачки функции распределения:p(x)=F(x⁺)-F(x) – это приращение или скачокфункции в точкеx.

2) Непрерывные случайные величины (абсолютно непрерывные).

Это означает, что X– абсолютно непрерывная или непрерывна относительно линии Лимберга, еслиP(XА)=0 для любого А:(A)=0 – множество мер.

Если мера абсолютно непрерывна относительно меры Лимберга, то существует такая функция p(x) – плотность распределения, чтоp(xA)=p(x)dx. Непрерывнойxназывается такая величина, которая имеет плотность распределения:

F(x)=P(X(-,x))=(1)

p(x) – такая функция для которой выполняется условие (1)

Если р – будет непрерывная функция, то F(x) будет дифференцируема, тогдаF`(x)=p(x)

Свойства плотностей распределения:

1. p(x)>0 – т.к. функцияF(x) не убывает, аp(x)=F`(x)

1. 

мы писали, что p(xА)=_AP(x)dx, если в качествеAвзять всю вещественную прямую, тогда

Многомерные плотности распределения:

1. Вектор дискретного типа.

Тогда p(x₁,…,x_n)=P(X₁=x₁,…,X_n=x_n) – непрерывна на счетном множестве.

Свойства:

1. p(x₁,…,x_n)>0

2. p(x₁,…,x_n)=1 аналогичны свойствам случайного вектора.

2. Вектор непрерывного типа.

Случайный вектор имеет непрерывное распределение, если p(xА)=0, если мера Лимбела(A)=0, тогда существует такая плотность распределения , что

1. P(xА)=…p(x₁,…,x_n)dx₁…dx_n– эта функция – есть плотность распределения случайного вектора.

Связь с F(x₁,…,x_n):

(2) F(x₁,…,x_n)=P(xА)=P(x(-,x₁),…,x(-,x₁))=p(t₁,…,t_n)dt_n

Если в качестве А можно взять такое множество, то по формуле (1) получим (2).

Связь с p(x₁,…,x_n):

Это есть смешанная производная: p(x₁,…,x_n)=(ⁿ/(x₁…x_n))F(x₁,…x_n)

Свойства:

1. p(x₁,…,x₂)>0 – это есть производная отF

2. …p(x₁,…,x_n)dx₁…dx_n=1

Если все агрументы x_iустремить к, то тогда пределF(x₁…x_n)=1

12. Примеры известных распределений.

1. В формуле Бернулли m– число успехов

m– это и есть случайная величина. У насэлементов вероятностного пространства={0,1…,0,1}

0 – неудача, 1- успех.

Число успехов m=m() – это и есть случайная величина. Она дискретного типа, т.к. принимает конечное число значений.

Функция распределения F(x)=P(m<x)

В точке 0 – скачок, величина равна p₀=p(m=0)=qⁿ, затем скачок в точке 1, величина равнаp₁=p(m=1)=C_n¹pq^n-1и т.д.

Последний скачок будет равен 1 это сумма всех вероятностей.

2. Когда схема Бернулли состоит из 1-го испытания (n=1), тогда случайная величинаxлибо 0, либо 1.

P(x=1)=p

P(x=0)=1-p=q– Бернуллевская случайная величина.

3. Пуассоновская случайная величина, задается с помощью распределения.

P(x=k)=,k=0,1,2…>0 - распределение Пуассона

Вспомним теорему Пуассона.

P_n(k),=np

Биноминальное распределение в пределе становиться Пуассоновским, т.к. p(x_n=k)P(У=k)P(У=k) – Пуассоновская случайная величина.

4. Геометрические вероятности.

Берем случайным образом точку х – это есть случайная величина на интервале [0,1], можно рассмотреть вероятностное поле, тогда p(xА)=(A).

P(xА)=(A[0,1])

F(x)=P(X<x)=((-,x)[0,1]), будет записываться по разному, в зависимости от того где находитсяx.

Эта величина имеет плотность распределения P(x)=

Такая случайная величина – равномерная случайная величина, а распределение - стандартное равномерное.

Если точка находится на произвольном интервале [a,b], в этом случаеP(xА)=(A[a,b])/([a,b]),

тогда F(x)=,

тогда

,

P(x)=- Это общее равномерное распределение.

Случайные величины могут задаваться плотностью распределения.

5. Нормальная случайная величина с параметрами a,²:N(a,²) имеет плотность распределения:

p(x)=

Если а=0, ²=1, тоp(x)=

Случайная величина с такой р(х) называется стандартной нормальной случайной величиной.

Вспомним интегральную теорему Муавра-Лапласа:

Мы доказали, что P(<x)Ф(х)=- функция распределения стандартной нормальной случайной величины. Т.е. если мы возьмемx_n=, тогдаP(X_n<x)P(Y<x)

Распределение величины Yимеет стандартное нормальное распределение.

6. Пусть существует x₁,…,x_n– независимые случайные величины.

p(x₁)…p(x_n) – их плотности, тогдаp(x₁,…,x_n)=П₁ⁿp_i(x_i)

Если представить, что случайные величины имеют равномерное распределение

x_i,i<nна [0,1] и независимы, т.е.P(x)={1,x[0,1]; 0,x[0,1]}, тогда случайный вектор будет иметь равномерное распределение вn-мерном кубе.

P(x₁,…x_n)={1, если всеx_i[0,1]; 0, если хотя бы 1x_i[0,1]}

13. Случайные векторы, их распределения. Независимые случайные величины.

Случайные векторы:

X:R¹

Случайный вектор X=(x₁,x₂, …,x_n) – векторы из случайных величин, он отображаетRⁿ

Случайный вектор – это есть измеримое отображение Rⁿ

В Rⁿ–другой набор барелевских множествBⁿ, т.е. надо взятьBⁿ, тоX^-1(B)F

В R²–B– это прямоугольники, ВR³–B– это параллелепипеды

Распределение в Rⁿ:

Если Bⁿ, тоq()=P(XB)

q(A)=P(XA),AВⁿ– распределение. Посмотрим, что в случае случайных величин, распределение характеризуется функцией распределения:

F(x)=P(X<x) – и для векторов.

Если X=(x₁,x₂, …,x_n), то функция распределения будет функциейnаргументов:

F(x₁, x₂, … ,x_n)=P(X₁<x₁, …, X_n<x_n).

Барелевские множества рассчитываются прямоугольником.

Вероятность попадания случайнойdвеличины в этот прямоугольник.

Функция распределения, тогда для n=2,c(двумерное множество).

ab

Функция распределения - это полубесконечный заштрихованный прямоугольник

P(XS)=F(b,d)-F(b,c)-F(a,d)+F(a,c), по аддитивности вероятности можно сложить также формулы и получитьp.

Само вероятностное пространство не важно для единичной случайной величины.

Для вектора важно распределение этого вектора и не важно вероятностное пространство.

Свойства функции распределения случайного вектора:

1. F(x₁,…,x_n)[0,1]

2. F(x₁,…,x_n) не убывает по каждому из аргументов. Доказательство такое же как и для случайной величины.

3. F(x₁,…,x_n) непрерывно слева по каждому аргументу.

4. Lim_xi-F(x₁,…,x_n)=0 доказательство такое же.

5. Lim_xiF(x₁,…,x_n)=F_{x1,…,xi-1,xi+1,…,xn}(x₁,x₂,…x_i-1,x_i+1,…,x_n)

Пусть F(x₁,…,x_n)=P(X₁<x₁, …,X_n<x_n) еслиx_iэто условиеX_i<x_iисчезнет, по условию непрерывности, тоx_i– конечная величина, поэтому эта величина приx_i=

P(X₁<x₁,…,X _i-1<x_i-1,X _i+1<x_i+1,X_n<x_n) – это есть функция распределения=F_{x1,…,xi-1,xi+1,…,xn}(x₁,x₂,…x_i-1,x_i+1,…,x_n).

Последовательно переходя к пределу, если все аргументы стремятся к , то

limF(x₁,…,x_n)=1

Независимые случайные величины:

Определение:независимость случайных величин.

Две случайные величины xиyназываются независимыми, если событие {xА} и {yB} независимы при любыхAиB:A,BВ

Это означает что вероятность того, что P(xА,yB)=P(xА)P(yB) – произведение вероятностей.

Пусть есть случайные величины x₁,x_2,…,x_n– они называются независимыми если события {x₁А₁}…{x_nА_n} независимы в совокупности дляA₁…A_nB

Вероятность того, что P(x₁А₁,… ,x_nА_n)=P(x₁А₁)…P(x_nА_n)

Как характеризовать независимость случайных величин. Пусть есть случайный вектор, компоненты которого независимы, тогда

F(x₁,…,x_n)=P(X₁<x₁, …,X_n<x_n), т.к. они независимы между собой =P(X₁<x₁)…P(X_n<x_n)=F(x₁)…F(x_n) (3)

F_i(x_i) – функция распределенияx_i

Таким образом, если случайные величины не зависимы, то совместная функция распределения = произведению функций распределения компонент.

Обратно верно: если совместная функция распределения распадается в произведение функций распределения компонент, то эти величины независимы.

Независимость в терминах плотностей:

Если мы возьмем смешанные производные от произведения, то

p(x₁,…x_n)=p₁(x₁)…p_n(x_n) (4)

Верно и обратное, если выполнено (4), то выполняется и (3).

Действительно, если верно:

F(x₁,…,x_n)=p(t₁,…,t_n)dt_n==F₁(x₁)….F_n(x_n)

Независимость означает, что совместная плотность распределения есть произведение плотностей.

14. Теорема о плотности распределения преобразованного случайного вектора. Примеры применения.

1. Преобразование случайных величин.

Пусть существует X– случайная величина с плотностью распределенияp(x).

Пусть y=(x) – некая функция от случайной величины с плотностью распределенияq(x).

Как можно q(x) выразить черезp(x)?

Пусть (x) – дифференцируема и монотонна, т.е. междуyиxсуществует взаимно однозначное соответствиеyx

Пусть (x) – монотонно возрастающая, тогда

P(Y<x)=P((x)<x)=P(X<^-1(x))=F(^-1(x))

q(x)=(F(^-1(x))`=p(<sup>-1</sup>(x)(<sup>-1</sup>(x))`=P(^-1(x))/`(<sup>-1</sup>(x)), т.к.- монотонная,` будет > 0.

Если (x) убывает, то аналогично мы получим:

q(x)= -P(^-1(x))/`(^-1(x))

Общая функция: q(x)=P(^-1(x))/|`(^-1(x))|

^-1(x) – обратная функция.

Примеры:

1. Пусть (x)=aX+b

^-1(y)=^y-b/_a

(^-1(y))`=¹/_a

q(y)=¹/_|a|p(^y-b/_a)

2. P(x)=

y=e^-x

(x)=y=e^-x

^(y)=-ln y

(^-1(y))`=-¹/_y

q(y)=¹/_yP(-lny)=¹/_ye^{-ln y}=1, если 0<y<1; 0 в противном случае.

2. Случай случайного вектора.

Пусть :RⁿRⁿ– отображение.

Пусть - отображение взаимно однозначно, дифференцируема и выполняется условие теоремы о замене переменных в интеграле.

Пусть X– вектор с плотностью распределенияp(x).

Пусть Y=(x) случайный вектор с плотностью распределенияq(x).

q(y)=P(^-1(y)|J_^-1(y)|=P(^-1(y))/|J_(^-1(y))|

|Y_^-1(y)|=определитель матрицы состоящий из частных производных (якобиан преобразования).

Доказательство:

По теореме о замене переменных.

P(yА)=_Aq(y)dy=P((x)А)=P(x^-1(A))=_(A)p(x)dx= по теореме о замене переменных =_Ap(^-1(y))|J_^-1(y)|dy

^-1(A) – это множество тех точек, которые с помощью преобразованияпереходят в множество А (прообразы), т.е. все это верно для любого множества А, тогда

q(y)=p(^-1(y))|J_^-1(y)| ч.т.д.

Частный пример:

Линейное преобразование.

Y=AX+b,A– матрица,b– вектор, тогда

x)=AX+b

^-1(y)=A^-1(Y-b)

J_^-1(y)=¹/_det|A|

q(y)=¹/_|detA|p(A^-1(Y-b))

Пример:Стандартный нормальный вектор

p(x)=

Y=Ax+b– невырожденный нормальный вектор, который получается с помощью такого преобразования, и |A|0.

q(y)==

пусть R=A^TA, R^-1=(A^-1)^TA^-1

detR=(detA)²

=

15. Нормальные случайные величины и векторы.

Нормальная случайная величина:

Нормальная случайная величина с параметрами a,²:N(a,²) имеет плотность распределения:

p(x)=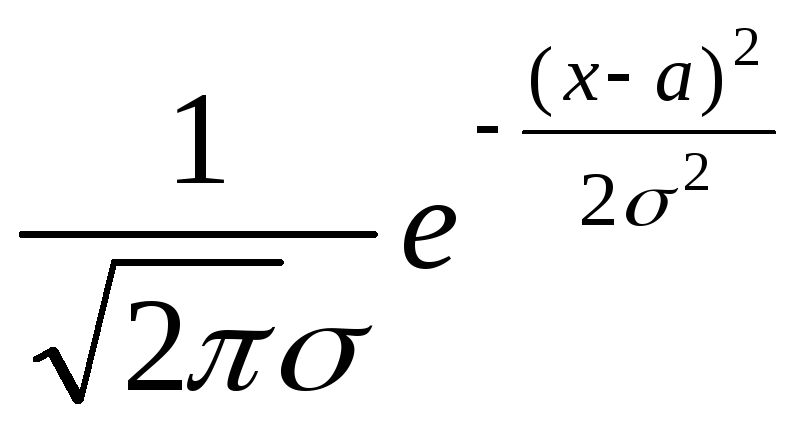

Если а=0, ²=1, тоp(x)=

Случайная величина с такой р(х) называется стандартной нормальной случайной величиной.

Вспомним интегральную теорему Муавра-Лапласа:

Мы доказали, что P(<x)Ф(х)=- функция распределения стандартной нормальной случайной величины. Т.е. если мы возьмемx_n=, тогдаP(X_n<x)P(Y<x)

Распределение величины Yимеет стандартное нормальное распределение.

График cтандартного нормального распределения имеет вид:

Чем меньше тем более острый пик.

_

_₂<<₁

Локальная теорема Муавра-Лапласа – может довести до сходимости плоскости стандартного распределения.

Пусть компоненты вектора p_i(x_i)=- имеет нормальное распределение, тогдаP(x₁,…x_n)=(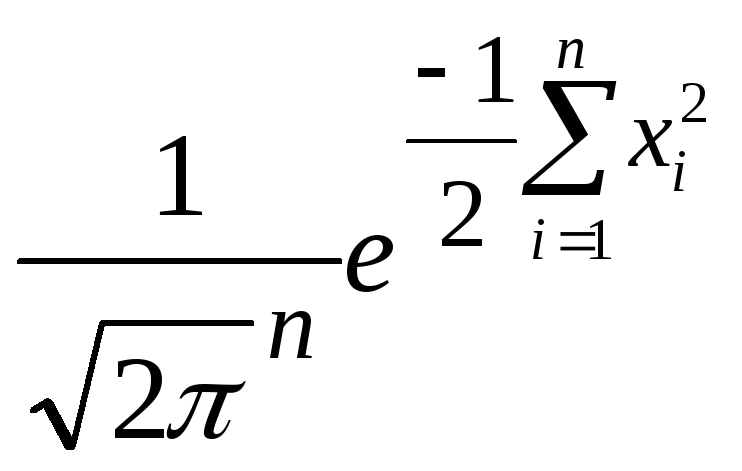), если аргумент записать какX=(x₁,…,x_n), тогдаp(X)=- такой вектор называется стандартным случайным нормальным вектором.

Пример:Стандартный нормальный вектор

p(x)=

Y=Ax+b– невырожденный нормальный вектор, который получается с помощью такого преобразования, и |A|0.

q(y)==

пусть R=A^TA, R^-1=(A^-1)^TA^-1

detR=(detA)²

=

16. Мат. ожидание и его свойства.

Дискретная случайная величина:

Существует прямая, значения возможных случайных величин и вероятности, с которыми они принимаются. Пусть случайная величина – это физическое тело.

x₁x₂x₃x_n



p₁p₂p₃p_n

Сумма всех p_i=1

Материальное тело заменяется на точечное.

^_i=1x_ip_i– математическое ожидание – в теории вероятности некая характерная точка для всей случайной величины, вокруг которой сосредоточены все остальные (центр масс, центр тяжести).

Непрерывная случайная величина

Вещественная прямая – некая материальная линия и p(x) – плотность распределения массы

этой линии Центр массы- мат. ожидание для непрерывной величины.

В физике рассматривают моменты ,^_i=1x_i^kp_i–k-ый момент случайной величины.

Аналогично, если ставить |x_i^k|p(x)dx–k-ый абсолютный момент.

Определение математического ожидания:

Пусть существует Х – случайная величина – это функция от :X().

Мат. ожидание случайной величины X:EX=_x()dPабстрактный интеграл Лимбела.

Отсюда вытекают свойства мат.ожидания, которые являются войствами интеграла.

Свойства математического ожидания:

1)Аддитивность:

E(X+Y)=EX+EY

2) E(X)=EX- вещественное или комплексное число

3) EX>0, еслиx>0

4) Если х>0 иEX=0, то х=0cвероятностью 1

1, 2, 3 свойства интеграла.

5) Пусть x,y- случайные величины, независимы и у них существует Е, тогдаEXY=EXEY

Доказательство:(только для непрерывных).

Т.к. x,y– независимы и непрерывны, тоp(x,y)=p₁(x)p₂(y), тогдаxy=(x,y)

EXY===можно разбить на произведение интегралов ==EXEY

6) Eконстанты равно самой константе:Ec=c.

Как выглядит Eдля непрерывных и дискретных величин:

Пусть х – дискретная величина x₁x₂x_n

p₁p₂ p_n

EX=_x()dP(1)

Разобьем на множества:=_n{:X()=x_n)=_nA_n– множества А_nне пересекаются и дает в сумме, поэтомуEможно разбить на сумму интегралов.

EX=_x()dP=_n_nx()dP=*

на каждом А_n:X()=x_n

*=_n_n x_n dP=_nx_n _n dP=_nx_np_n.

- когдаX– случайная дискретная величина.

Если xнепрерывная случайная величина, которая имеет плоскость распределенияp(x), то сделаем в интеграле (1) замену переменных: воспользуемся отображением Х:R¹, тогда интеграл перейдет в интеграл по вещественной прямой.

EX=_x()dP=_R1xdq(x)=_R1xp(x)dx,q– это распределение:dq(x)=p(x)dx.

Поэтому в непрерывном случае:

- когда х – непрерывная случайная величина.

17. Мат. ожидание функции от случайной величины.

Лемма:Пусть есть х – случайная величина и непрерывная функциянадо найтиEx).

1. E(x) можно вычислять по формуле:E(x)=^_i=1(x_i)p_i– для дискретных случайных величин.

E((x))=- для непрерывной случайной величины.

2. Пусть существуют x,y– 2 случайные величины, существует(x,y), тогда

E(x,y)=_i,j(x_i,y_j)p_ij, гдеp_ij=p(x=x_i,y=y_j) для дискретных случайных величин.

E(x,y)=илиE(x,y)=для непрерывной случайной величины.

Доказательство:(только для двух случайных величин)

1. Для дискретного случая

E(x,y)==*

A_ij={:x=x_i,y=y_j};P(A_ij)=p_ij, по аддитивности *=_i,j(x_i,y_i)p_ij

2. В случае непрерывных случайных величин:

E(x,y)=_(x,y)dP=_R2(x,y)dq(x,y)=

dq(x,y)=p(x,y)dxdy

18. Примеры вычисления мат.ожиданий для известных распределений.

1. Пусть х имеет распределение Бернулли, т.е.

EX=1p+0q=p

2. Пусть х имеет биноминальное распределение, т.е. k– число успехов в серии изnнезависимых испытаний, где вероятность успеха при одном испытании =p.

x– случайная величина с вероятностьюp_k=C_n^kp^kq^n-k.

EX=ⁿ_k=0x_kC_n^kp^kq^n-k.

Введем последовательность случайных величин.

тогдаx=ⁿ_k=0x_k, в силу (1) свойстваE

EX=ⁿ_k=0 Ex_k=np, т.к. каждаяx_k– есть случайная величина Бернулли, вероятность которой=p

3. Пусть x– имеет распределение Пуассона, т.е.

P(x=k)=,>0,k=0,1,2…

EX===e^-e^=, т.к.=e^

4. Пусть x– имеет равномерное распределение на интервале [a,b] т.е.

EX= - центр масс стержня.

5. Нормальное распределение.

P(x)==сделаем заменуx-a=y

+

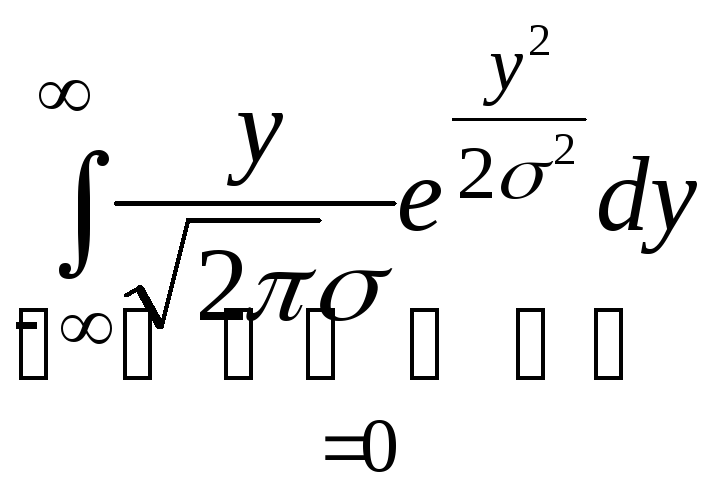т.к. под интег- т.к. это есть

ралом нечет- интеграл от

ная функция плотности

нормального

закона =1

Значит в нормальном распределении EX=a

19. Дисперсия, ее свойства.

По определению DX=E(X-EX)²– мат.ожидание от квадрата отклонения мат.ожиданияx. Это второй центральный момент относительно мат. ожидания.

Смысл: если Е – центр, вокруг которого распределены случайные величины, то D– указывает на степень концентрации величин вокругx– степень рассеивания х.

Свойства дисперсии:

1. DX>0 т.к. y=(x-EX)²>0 => Ey>0 => DX>0

2. DX=0 тогда и только тогда, когдаX=EXcвероятностью 1, это свойство Е т.кy=X-EX=0

3. DC=0 т.к. EC=C => C-EC=0

4. D(CX)=C²DX, т.к. D(CX)=E(CX-E(CX))²=E(C(X-EX))²=C²E(X-EX)=C²DX

5. Если x,y– независимы случайные величины, тоD(x+y)=Dx+Dy– это распространяется на любое число независимых случайных величин.

а) Будем предполагать, когда EX=EY=0

D(X+Y)=E(X+Y)²=EX²+EY²+2EXY=EX²+EY², т.к. независимы, то 2EXY=EXEY=0

б) EY0, тогда введем вспомогательную величину:

x`=X-EX,y`=Y-EY, уx` иy`EX`=0 иEY`=0, поэтомуD(X`+Y`)=DX`+DY`.

Т.к. D(X+Y)=D(X`+Y`) =>DX=DX` иDY=DY`.

6) D(X+C)=DX, C=const

E(X+C)=EX+C

D(X+C)=E(X+C-EX-C)²=E(X-EX)²=DX

7) D(X+Y)<2(DX+DY), для зависимых величин.

Надо доказать, что: E(X+Y)²<2(EX²+EY²), верно что (X+Y)²<2(X²+Y²), откуда получаемE(X+Y)²<2(EX²+EY²).

Если раскрыть скобки, то получим, что (X-Y)²>0

8) Для вычисления дисперсии используют формулу:

DX=EX²-(EX)²

DX=E(X-EX)²=E(X²-2XEX+(EX)²)=EX²-2EXEX+(EX)²=EX²-(EX)²

20. Примеры вычисления дисперсии.

1. Пусть х имеет распределение Бернулли, т.е.

EX²=EX=p, поэтому DX=p-p²=p(1-p)=pq

2. Пусть х имеет биноминальное распределение, т.е. k– число успехов в серии изnнезависимых испытаний, где вероятность успеха при одном испытании =p.

x=ⁿ_k=1x_k, т.к. испытания независимы, то дисперсия суммы равна сумме дисперсий.

D(X_k)=pq=>DX=npq

3. Пусть x– имеет распределение Пуассона, т.е.

P(x=k)=>0,k=0,1,2…

EX²=====e^-(e^+e^)=^+, т.к.=e^

DX=EX²-(EX)²=²+-²=

При распределении Пуассона и мат.ожидание, и дисперсия равны .

4. Пусть x– имеет равномерное распределение на интервале [a,b] т.е.

EX²=

DX=EX²-(EX)²=¹/₃(b²+ab+a²)-¼ (b²+2ab+a²)=¹/₁₂(b-a)²

5. Нормальное распределение.

p(x)=

DX==E(X-EX)²=E(X-a)²=, сделаем замену (x-a)/=y=>

===²

интегрируем по частям, а потом интеграл от плотности.

21. Коэффициент корреляции, его свойства.

Третьей характеристикой является совместная характеристика поведения двух случайных величин – корреляция:

cov(x,y)=E((X-EX)(Y-EY))

Коэффициент корреляции (1)

Если они независимы, то (x,y)=0, иногда(x,y)=0 и для зависимых величин.

Свойства ковариации и коэффициента корреляции:

1. cov(x,y) и(x,y) не зависят от сдвига случайных величинxиy. Это означает, что если мы рассмотримx`=x+cиy`=y+c, тоcovибудут у этих двух величин одинаковые.

cov(x`,y`)=cov(x,y), (x`,y`)=(x,y)

Доказательство:из определения;

Если xприбавить с, то и к Е прибавиться с, поэтомуx`-E`=x-Exи аналогично дляy.

Дисперсии не зависят от сдвига.

2. (x,y) не зависит от масштаба.

Доказательство:

Пусть х`=xиy`=y, где>0, тогдаcov(x`,y`)=cov(x,y)

Dx`=<sup>2</sup>Dx,Dy`=^Dy, подставляя в формулу (1) получаем, что(x`,y`)=(x,y)

Замечание:Еслиxумножить на положительное число, аyна отрицательное, то модульне измениться, а знак станет противоположным.

3. Если x,y– независимы, тоcov(x,y) и(x,y) = 0

Достаточно доказать, что cov(x,y)=0

Доказательство:

Пусть EX=EY=0, т.к.covине зависят от сдвига.

Если x`=x-EXиy`=y-Ey, то ковариация останется прежней, в этом случаеcov(x,y)=EXY=EXEY=0

Обратное не верно.

Пример:Пустьxслучайная величина с нормальным распределением:

P(x)=, аy=x²

Тогда cov(x,y)=E(X(Y-EY)=EXY-EXEY=EX³-EXEX², у такого распределенияEX³=0 иEX²=0, поэтомуcov(x,y)=0

4. cov(x,y)=EXY-EXEY

5. –1<(x,y)<1

Если ||=1, тоx,y– линейно зависимы, т.е.x=ay+b, гдеa,b–const, причем если:

=1, то a>0

то a<0

Это свойство позволяет сказать, что - это мера зависимости линейной случайной величины.

Доказательство:

Отсюда во всех случаях 1+(x,y)>0, отсюда –1<(x,y)<1

Это выражение равно 0, когда 0, поэтому имеется линейная зависимостьXиY.

Если =1, то знак, -a<0

Если =-1, то знак, +a>0 ч.т.д.

Пример:

1. Пусть u₁,u₂,…,u_n– независимые случайные величины, одинаково распределены.

Мат. ожидание всех величин = 0.

²– дисперсия (одинаковая).

Пусть x=u₁+u₂+…+u_mn>m

y=u₁+u₂+…+u_n

Чему равняется covи

cov(x,y)=E(u₁+u₂+…+u_m)(u₁+u₂+…+u_n)=E(u₁+u₂+…+u_m)²+E(u₁+u₂+…+u_m)(u_m+1+u_m+2+…+u_n)=

E(u₁+u₂+…+u_m)²– дисперсия

E(u₁+u₂+…+u_m)(u_m+1+u_m+2+…+u_n) – это независимые величины, поэтому = 0

^m+E(u₁+u₂+…+u_m)E(u_m+1+u_m+2+…+u_n)=^m

т.е. DX=^m,DY=²n

(x,y)=

2. Кубик бросается до первого появления четного числа.

x=n– число бросаний

y– значение при последнем броске.

Найти cov(x,y)

Оказывается cov(x,y)=0, т.к.x,y– независимы.

P(y=2i)=¹/₃, i=1,2,3 – y – четное

P(x=n)=¹/2^n-1½ =¹/2ⁿ

P(x=n,y=2i)= ¹/2^n-1¹/₆ =¹/2ⁿ¹/₃

3. Многомерное нормальное распределение.

X=(x₁,x₂,…,x_n) – независимые компоненты и имеют нормальное распределение.

p_i(x)=

Совместная плотность распределения

p(x)==

Y=Ax+bбудем предполагать, чтоAне вырожденная.

R=AA^T

q(x)=

EY=AEX+b

EX=0, поэтому EY=b, EY_i=b_i

Y_i=ⁿ_k=1a_ikX_k+b_i

Пусть b_i=0.

cov(y_i,y_j)=E((ⁿ_k=1a_ikX_k)(ⁿ_m=1a_jmX_m))=ⁿ_k=1ⁿ_m=1a_ika_jmEX_kX_m= если km =0, т.к. независимы

Т.к. b_i=0, следовательноEX_k=0

Остается k=m

ⁿ_m=1a_ima_jm=Dxнормального вектора=1 поэтомуEX_k²=1.

С другой стороны эта сумма = (AA^T)_ij=R_ij

Матрица Rсостоит из ковариаций.

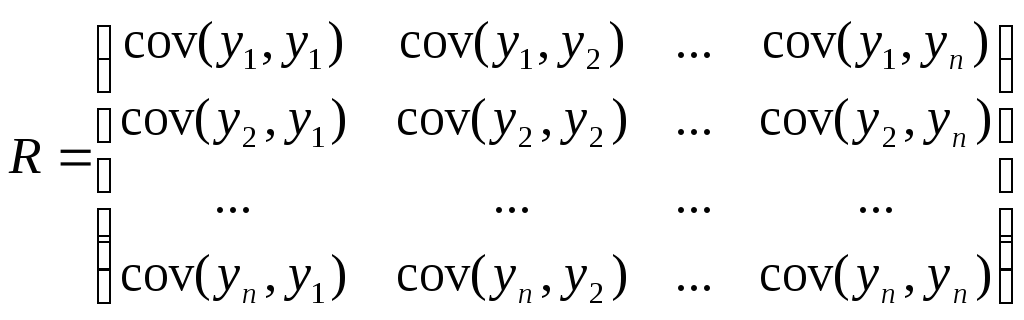
Ковариационная матрица нормального вектора.

6. Неравенство Чебышева и закон больших чисел.

Пусть существует y– случайная величина>0, у которойEy<- конечна,

Тогда P(y>)<^Ey/_- одно из неравенств Чебышева.

Док-во:Найдем вспомогательную случайную величину:y₁=y||_y>

||_y>- индикатор

тогда можем написать неравенство: y₁<y, т.е. еслиy>- то отсюдаP(y>)<Ey₁<Ey, но с другой стороныy₁>, поэтомуP(y>)<Ey₁

т.к. y₁0, можно заменить это множество на

y₂={,y>; 0y<)

y₂<y₁, аy₂– дискретная случайная величина, поэтомуEy₂<Ey₁

Ey₂=P(y>)

Замечание:Пусть мат. ожиданиеEe^y<- конечно, тогдаp(y>)=P(e^y>e^)<Ee^y/e^- это неравенства Чебышевского типа.

Одно из неравенств носит название Чебышева:

Пусть DX<, тогдаP(|X-EX|>)<DX/² (*)

Доказательство:Возьмем в качествеy=(X-EX)², в качестве=², тогдаP((X-EX)²>²)<E(X-EX)²/^=DX/²

P((X-EX)²>²)=P(|X-EX|>), из этого следует неравенство Чебышева (*), ч.т.д.

Определение:

1) Говорим, что последовательность случайных величин X_nсходится кXпо вероятности Р:

X_n^pX, если для любого>0:P(|X_n-X|>)0 приn.

Это означает, что сходимости может не быть, вероятность больших отклонений очень маленькая.

2) Мы говорим, что X_nсходится к Х среднеквадратично еслиE(X_n-X)²0 приn.

Среднеквадратичная сходимость принята в физике: смысл (энергетический, мощностной)

Свойство:

Из сходимости в среднеквадратичности следует сходимость по вероятности.

Доказательство:

Это следует из неравенства Чебышева.

P(|X_n-X-E(X_n-X)|>)<D(X_n-X)/²

Пусть E(X_n-X)=0, тогда из неравенства ЧебышеваD(X_n-X)/²0, тогдаP(|X_n-X|>)0.

Если E(X_n-X)0, то можно показать, чтоE|X_n-X|<, т.е.E(X_n-X)0.

Определение:

Еще один тип сходимости – слабая сходимость – это сходимость распределения.

Мы говорим, что X_nслабо сходится кX, еслиF_n(x)F(x) в каждой точке непрерывности функцииF(x), гдеF_n(x) иF(x) функции распределенияX_nиX.

Свойство:

Если есть сходимость по вероятности, то есть и слабая сходимость.