Билет №1.

Теоретическая и выборочная функция распределения.

Определение выборочной (эмпирической) функции распределения: Пусть

- выборка из распределения, задаваемого функцией распределения F(x). Будем считать, что - независимые случайные величины, определённые на

некотором пространстве элементарных исходов Ω. Пусть . Определим случайную величинуследующим образом:

,

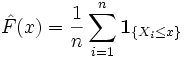где - индикатор события A. Таким образом выборочная функция распределения в точке x равна относительной частоте элементов выборки, не превосходящих значение x. Случайная величинаназывается выборочной функцией распределения выборки.

Функцию распределения F(x) наблюдаемой случайной величины ξ в этом случае называют теоретической функцией распределения.

Основные св-ва:

Пусть зафиксирован элементарный исход . Тогдаявляется функцией распределения дискретного распределения, задаваемого следующей функцией вероятности:

,

где x_i = X_i(ω), а 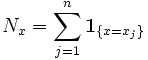- количество элементов выборки, равных x. В частности, если все элементы выборки различны, то.

Математическое ожидание этого распределения имеет вид:

.

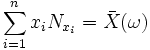Таким образом выборочное среднее - это теоретическое среднее выборочного распределения.

Аналогично, выборочная дисперсия - это теоретическая дисперсия выборочного распределения.

Случайная величина имеет биномиальное распределение:

.

Выборочная функция распределения является несмещённой оценкой функции распределения F(x):

.

Дисперсия выборочной функции распределения имеет вид:

.

Согласно усиленному закону больших чисел, выборочная функция распределения сходится почти наверное к теоретической функции распределения:

почти наверное при .

Выборочная функция распределения является асимптотически нормальной оценкой теоретической функции распределения. Если , то

по распределению при .

Билет №2.

Теоремы Гливенко и Калмогорова о сходимости выборочной функции.

Теорема(1.):ПустьF_n(x) – эмпирическая функция распределения , построенная по выборкеХ=(Х₁,Х₂…..Х_n) из распределенияZ(ξ) – соответствующая теоретическая функция распределения. Тогда для любого х (-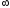<x<+) и любого

.

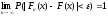Теорема Гливенко: В условиях теоремы(1.)

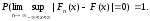
Другими словами, это соотношение означает, что отклонение

эмпирической функции распределения от теоретической на всей оси с вероятностью 1 будет сколь угодно мало при достаточно большом объёме выборки.

Теорема Колмогорова:Если функцияF(x) непрерывна, то при любом фиксированномt> 0

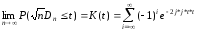
При этом предельную функцию распределения K(t) можно с хорошим приближением использовать для практических расчетов уже приn≥20.

__________________________________________________________________________

Билет №3.

Сходимость выборочных характеристик к теоретическим. Примеры

Теорема1:Пусть— выборка объемаиз неизвестного распределенияс функцией распределения. Пусть— эмпирическая функция распределения, построенная по этой выборке. Тогда для любого

Теорема Гливенко — Кантелли.Пусть— выборка объемаиз неизвестного распределенияс функцией распределения. Пусть— эмпирическая функция распределения, построенная по этой выборке. Тогда

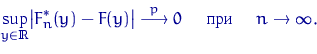
Более того, в условиях теорем 1 и Гливенко — Кантелли имеет место сходимость не только по вероятности, но и почти наверное.

Билет №4.

Гистограмма как выборочный аналог теоретической плотности.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению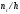(плотность частоты).

Площадь i-го частичного прямоугольника равна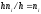- сумме частот вариантi-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению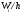(плотность относительных частот)

Билет №5.

Состоятельность, асимптотическая нормальность, асимптотическая несмещенность, асимптотическая несмещенность оценок.

Оценки смещение которых убывает при увеличении объема выборки и в пределе, при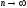становятся несмещенными.

Пусть X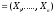выборка из распределения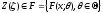, где параметрическое множество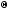в общем случае некоторый невырожденный открытый интервалr-мерного евклидова пространства. По определению, оценка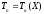для заданной параметрической функцииназывается состоятельной, если при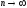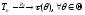, т.е., каково бы ни было истинное значение параметр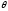а, оценкасходится по вероятности к истинному значению оцениваемой функции.

Билет №6.

Примеры несмещённых и смещённых оценок.

Определение: Пусть — выборка из распределения, зависящего от параметра. Тогда оценканазывается несмещённой, если

.

В противном случае оценка называется смещённой, и случайная величина называется её смещением.

Примеры:

Выборочное среднее является несмещённой оценкой математического ожидания X_i, так как если, то.

Пусть случайные величины X_iимеют конечную дисперсию DX_i= σ2. Построим оценки

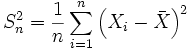— выборочная дисперсия,

и

— исправленная выборочная дисперсия.

Тогда является смещённой, а S²несмещённой оценками параметра σ2.

Билет №7.

асимптотическая нормальность выборочной медианы, сравнение асимптотической эффективности среднего и выборочной медианы.

Теорема - если в некоторой окрестности точки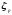плотностьf(x) непрерывна вместе с производной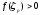 и, то при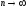: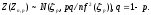Эта теорема описывает асимптотическое поведение для больших выборок, как говорят, средних членов вариационного ряда, т.е. порядковых статистик, номера которых удовлетворяют условию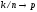при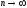, где 0<p<1. Таким образом для больших выборок из достаточно гладких распределений средние члены вариационного ряда асимптотически нормальны.

Для любой оценки 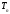, удовлетворяющей условию:, ее асимптотическая эффективностьeff(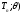определяется как отношение нижней границы Рао – Крамера к асимптотической дисперсии оценки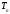:eff

Билет №8

Метод максимального правдоподобия: описание и примеры оценок.

Определение: Пусть есть выборка из распределения, где- неизвестный параметр. Пусть- функция правдоподобия, где. Точечная оценка

называется оценкой максимального правдоподобия параметра θ. Таким образом оценка максимального правдоподобия - это такая оценка, которая максимизирует функцию правдоподобия при фиксированной реализации выборки.

Примеры: Пусть - независимая выборка из непрерывного равномерного распределения на отрезке [0,θ], где θ > 0 - неизвестный параметр. Тогда функция правдоподобия имеет вид

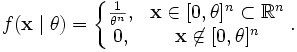
Последнее равенство может быть переписано в виде:

где , откуда видно, что своего максимума функция правдоподобия достигает в точке. Таким образом

.

Пусть - независимая выборка из нормального распределения с неизвестными средним и дисперсией. Построим оценку максимального правдоподобиядля неизвестного вектора параметров. Логарифмическая функция правдоподобия принимает вид

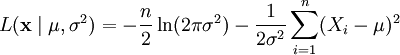
Чтобы найти её максимум, приравняем к нулю частные производные:

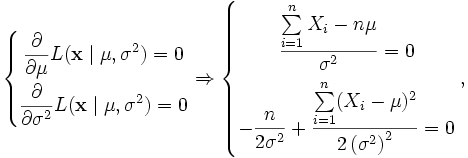
откуда

- выборочное среднее, а

- выборочная дисперсия.

*26-30

Билет №11.

Достаточные статистики, критерий факторизации.

Статистика T=T(X)(вообще говоря, векторная) называется достаточной для моделиF={F(x,),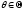} (или достаточной для параметра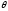когда ясно, о какой модели идёт речь), если условная плотность (или вероятность в дискретном случае)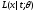случайного вектораX=(X₁,……,X_n) при условииT(X)=tне зависти от параметра.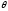

Это свойство статистики Tозначает, что она содержит всю информацию о параметре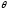, имеющуюся в выборке, и поэтому все заключения об этом параметре, которые можно сделать при наблюденииx, зависят только отt=T(x).

Критерий факторизации: Для того чтобы статистикаT(X) была достаточной для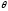, необходимо и достаточно, чтобы функция правдоподобияL(x;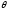) имела вид:

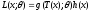, где множительgможет зависеть от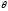, а отxзависит лишь черезT(x), множительhже от параметра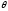не зависит.

Билет №13,14.

Полные статистики.

X,p(x,) – плотность, T – статистика

если из E_f(T(x))=0=>f(x)=0

Будем рассматривать полные достаточные статистики (ПДС), получим ограничение сверху и снизу.

Пример построения полной статистики

Если существует экспоненциальное распределение, то при определенных условиях T=(T₁,…,T_n) является полной статистикой.

Надо, чтобы в T_i_i(),_iбылоk-мерным, (₁()),…,_k()) отображалось вR^k.

1) Схема Бернулли

Предположим, что m– число успехов, является достаточной статистикой.

возьмем _m=0ⁿf(m)C_n^mp^mq^n-m=0q(0,1), нужно доказать, чтоf(m)=0

_m=0ⁿf(m)C_n^mZ^m=0,Z=^p/_q,Z(0,)

получается полином с коэффициентами = 0, т.к. C_n^m0, тоf(m)=0

2) Распределение Пуассона

Существует объем выборки n=1, тогда

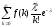=0уберемeполучим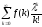=0, для>0¹/_k!0 =>f(k)=0

3) Равномерное распределение R(0,)

объем выборки n=1

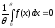получается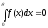=>f(x)=0 с вероятностью 1

Билет №15.

Свойства условных математических ожиданий.

1. Пусть X,Y– случайные величины.

p(x,y) – плотность распределения.

Определение: условная плотность распределения, при условии, что yфиксированое

p(x/y)=p(x,y)/p(y)

p(y+y<X<x+x/y<Y<y+y)=P(x<X<x+x,y<Y<y+y)/P(y<Y<y+y)=

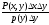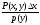==это можно брать в качестве условной плотности распределения

тогда мат.ожидание(условное) y-фиксированое

E(x/y)=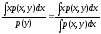

Рассмотрим мат.ожидание при условии, что какое-то событие A– фиксированое

E(x/A)==

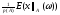
E(x/y) пустьA– не событие, а дискретно распределенная случайная величина, тогда

E(x/y)=E(x/A), где Y()=Y, А

Определение: Разбиением А множества называется набор подмножеств А из.

1. 

2. A_iА_j=, ij

E(x/A)=E(x/A_i), если А_i

E(x/A)=E(x/A) ||_Ai() - формальное определениеEпри условии разбиения

Условное мат.ожидание обладает всеми свойствами мат.ожидания + другие свойства.

Пусть существуют 2 разбиения А и В. Пусть А>B

Мы говорим, что А является более мелким разбиением, чем Bесли любой элемент разбиенияBявляется объединением элементовA.

Пусть B_i=_jA_ij

1. E(E(x/A)/B)=E(x/B)

2. E(E(x/B)/A)=E(x/B)

Т.е. всегда получается распределение вокруг более грубого распределения.

Доказательство:

2) Если B_i, тоE– одно и тожеyлюбогоA_ij, т.е.EB_iне зависит от выбораA_ij. Получается мат.ожидание постоянной и оно равно самой постоянной.

1) E(x/A_i)=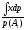

E(x/A)=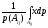

Предположим, что B_i=_jA_ij, построим внешнее

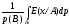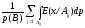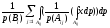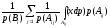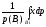=====E(x/B)

3. E(E(x/A))=Ex

4. Y- измеримо относительно разбиения {Y=y}А

E(XY/A)=YE(X/A)

Если E(X/A)=0, то E(X/Y)=0

Пусть существует конечное разбиение А, рассмотрим алгебру А (или -алгебру)

E(x/A)=E(x/F) мы можем по разбиению определить-алгебру и наоборот.

Можно определить мат.ожидание при условии алгебры, чтобы сохранились все свойства

Теорема: E(x/F) называется случайной величиной со следующими свойствами

1. _АЕ(x/F)dp=_Аxdpдля всехAF

2. E(x/F) – измеримо относительно А

Тогда определение мат.ожидания однозначно

Если взять x, то (2) свойство никогда не выполнится, х неизмеримо относительноF, т.к. измеримость однозначна.

E(x/F)<a)F

Билет №16.

Теорема о построении эффективных оценок

X, p(x,), S=S(x) – несмещенная для g(), T – ПДС, тогда S^*=E(S/T) – эффективная, несмещенная, c минимальной дисперсией, оценка.

Алгоритм нахождения эффективных оценок

1. Ищем T – ПДС

2. Ищем несмещенную оценку, являющуюся функцией от Т. Она и будет несмещенной оценкой.

Доказательство: Пусть существует несмещенная оценка SпостроимS^*=E(S/T), тогдаS^*- оценка, т.к.T– достаточная, она несмещенная, т.к.E_S^*=E_S(по свойствам условного мат.ожидания)

минимальная дисперсия

Пусть существует еще одна несмещенная оценка S₁, построимS^*=E(S₁/T), но тогда по по теореме

Рао-Блекуэлла D_S₁>D_S₁^*=D_S^*=> дисперсия любой другой оценки будет большеD_S^*

Осталось доказать DS₁^*=D_S^*

т.к. S^*иS₁^*совпадают с вероятностью 1, в силу полноты.

(S^*-S₁^*) они измеримы относительноT(т.к. мат.ожидание), т.е. являются функциями от Т. Они обе не смещены, поэтомуE(S^*-S₁^*)=0, значит в силу полнотыS^*-S₁^*=0 с вероятностью 1

Пример:

1. Экспоненциальное семейство:

(x, S²) – ПДС

=(m,²) – если хотим оценить

f(m,²) – достаточно построить несмещенную оценкуT.

2. Пусть x– выборка из распределения Бернулли.

x_i={1,p; 0,q}i<n,=p

m– число успехов – ПДС

оценка для p– несмещенная

x=^m/_n– частота – функция отmиp. =>x– это эффективная оценка.

Возьмем в качестве параметра функции g(p)=p²

S²=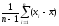- несмещенная оценка²

но в схеме Бернулли ^=pq=p(1-p)=p-p², т.е., чтобы оценитьs²надо иметь несмещенную оценкуp²,p²=^m/_n.

E_(S²)=pp²

p-E(S²)=p²если взятьT=^m/_n-S², тоET=p-p+p²=p², т.е. это не смещенная оценка.

S²====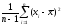

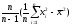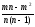
T=^m/_n-===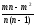

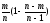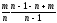получается несмещенная оценка, для p²

можно было не пользоваться S², а взятьx², т.к. (p=x) оценивают, тогдаp²=x²

Если мы оцениваем p^k, то несмещенной оценкой будет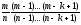

Билет №17.