Поведение, когда гипотезаневерна.

Предположим теперь, что и разбиениетаково, что

где вероятности вычислены по функции распределения. Тогда можно показать (см., например, [13, § 10.4]), что

если

(52)

Критерий проверки.

То обстоятельство, что поведение существенно различно в зависимости от того верна или нет гипотеза, дает возможность построить критерий для ее проверки. Зададимся некоторымуровнем значимости(допустимой вероятностью ошибки) и возьмем квантиль, определенную формулой (45):

Определим критическое множество:

Таким образом, наши действия по принятию (или отвержению) гипотезы состоят в следующем. Подстановкой имеющихся данныхв формулу (51) вычисляется значение функции, которое затем сравнивается с:

• если , то гипотезаотвергается(при этом говорят, что выборка обнаруживаетзначимое отклонениеот гипотезы),

• если , то гипотезапринимается(говорят, что выборкасовместимас гипотезой).

Действительно, такое решающее правило соответствует вышеизложенным фактам о поведении функции . Приведем аргументы, основанные на здравом смысле, свидетельствующие в пользу этого решающего правила. Если значения функцииоказались ``слишком большими'', то, принимая во внимание (52), разумно считать, что гипотезане имеет места. Если же значения``не слишком большие'', то, скорее всего, гипотезаверна, поскольку это согласуется с теоремой Пирсона.

При таком решающем правиле мы может допустить ошибку, отвергнув верную гипотезу . Из теоремы Пирсона вытекает, что при большихвеличина вероятности этой ошибки близка к.

Границы применимости критерия на практике.

Утверждения теоремы Пирсона и (52) относятся к пределам при.На практике, конечно, мы имеем дело лишь с выборками ограниченного объема. Поэтому, применяя вышеописанный критерий, необходимо проявлять осторожность. Согласно рекомендациям, изложенным в [7], применение критерия дает хорошие результаты, когда все ожидаемые частоты. Если же какие-то из этих чисел малы, рекомендуется, укрупняя некоторые группы, перегруппировать данные таким образом, чтобы ожидаемые частоты всех групп были не меньше десяти. Если числодостаточно велико, то, как указывается в книге, порог для ожидаемых частот может быть понижен доили даже до, еслиимеет порядок нескольких десятков.

Билет №30

Доверительный интервал и примеры. Доверительный интервал.

Существует выборка x₁ x₂ …x_nс плотностью распределенияP(x,) надо построить интервал с произвольными концамиP_(())=1-надо выбрать интервал покороче.

Например

Хотим построить доверительный интервал длm

²неизвестно

x– оценка дляm

отцентрируем (x–m), тогда дисперсия будет/m

(отнормировали)

распределение Т мы знаем

=>=>

Примеры

²неизвестно

;

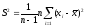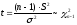
надо для tпостроить интервал

Если симметричен, то легко ограничить и получить маленький интервал

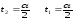
Можно брать по-разному, но сумма площадей хвостов=(т.е. 1/3и 2/3)

Пусть /2

;

= >

доверительный интервал:

Рассмотрим схему Бернулли

выборка 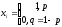хотим построить доверительный интервал для Р

воспользуемся законом больших чисел:

можно взять

=>

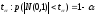
доверительный интервал:

Асимптотический доверительный интервал

Пусть 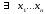n=2k+1

упорядочили

x_(k+1) – выборочная медиана

Выборочная медиана:

m

m совпадает с матожиданием

Какая оценка лучше?

x – лучшая оценка (x_(k+1)- хуже)

Выборочная медиана при нарушении основных предположений меняется мало, а x – сильно.

Пример

Пусть - плотность распределения Коши.

Характеристическая функция у x совпадает с характеристической функцией одного наблюдения (для Коши), т.е. информация о параметре вx такая же, как в одном наблюдении, т.е.x – несостоятельна. Ее нельзя применять, а- дает хорошую оценку.

Распределение Коши похоже на нормальное.

Сколько мы теряем, если распределение нормальное?

Построим доверительные интервалы. Какой короче?

1) По x :

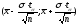
2) По :

, еслиx=, то

т.е. интервал длявбольше, чем дляx. Это асимптотически больше дляn.

Билет №31