29

Министерство образования Российской Федерации

ЮЖНО-РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

УНИВЕРСИТЕТ ЭКОНОМИКИ И СЕРВИСА

(ЮРГУЭС)

Методические указания

к самостоятельной работе по теме

“Элементы теории случайных процессов”

для студентов 2–3 курсов радиотехнических специальностей

Шахты 2002

Составитель

Син Л.И. Доцент кафедры математики ЮРГУЭС

Рецензент

Шрайфель И.С. Доцент кафедры математики ЮРГУЭС,

канд. физико-математических наук

Методические указания предназначены для оказания помощи студентам при выполнении расчетных заданий к типовому расчету по теме “Элементы теории случайных процессов”. Приведены подробные решения задач, однотипных задачам из сборника /7/. Приводятся все необходимые теоретические сведения из теории случайных процессов. В приложении приводятся необходимые для выполнения расчетных заданий табличные интегралы, формулы из теории вычетов. Методические указания составлены так, чтобы студент смог выполнить задания без обращения к дополнительной литературе. При желании студент может вычислять интегралы в математических пакетах, таких, какMATHCADилиMAPLE.

© Южно-Российский государственный университет экономики и сервиса, 2002

© Син Л.И., 2002

СОДЕРЖАНИЕ

Справочный теоретический материал………..…………………..4

Обозначения и сокращения.………………………………………………..4

1. Случайный процесс………….……………………………………………4

2. Математическое ожидание случайного процесса………………………4

3. Дисперсия случайного процесса…………………………………………5

4. Корреляционная функция случайного процесса…..…………….………5

5. Взаимная корреляционная функция случайного процесса.…….………6

6. Характеристики производной случайного процесса.….……..…………7

7. Характеристики интеграла случайного процесса…...………..…………7

8. Стационарные случайные процессы…….….………..………..…………8

9. Эргодическое свойство стационарного случайного процесса…………9

10. Спектральное разложение стационарного случайного процесса……..9

11. Преобразование стационарного с.п. стационарной

линейной динамической системой………………..…………………….10

РЕШЕНИЯ ЗАДАЧ………………………………………………….…...………..11

ПРИЛОЖЕНИЕ 1. Табличные интегралы…...………………….……..………...29

ПРИЛОЖЕНИЕ 2. Сведения из теории вычетов………………….…..…..…….31

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ………………………......….32

СПРАВОЧНЫЙ ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ

Обозначения и сокращения.

UN(m;) означает, что случайная величина U распределена по нормальному закону с математическим ожиданием m и дисперсией .

UR(a; b)  случайная величина U распределена равномерно на отрезке [a; b]. Математическое ожидание дисперсия .

UE(λ)  случайная величина U распределена по экспоненциальному закону с параметром λ. .

UВ(n, p)  случайная величина U распределена по биномиальному закону с параметрами n, p. .

UР(λ)  случайная величина U распределена по закону Пуассона с параметром λ. .

σ  среднеквадратическое отклонение,  дисперсия.

центрированная случайная величина или центрированный случайный процесс.

С. п. сокращение слов “случайный процесс”.

М. о. сокращение слов “математическое ожидание”.

1.Случайный процесс. ФункцияX = X (t,ω), гдеt T, (tвремя, илиt 0,Ωпространство элементарных событий) называетсяслучайным процессом. В дальнейшем с. п.X (t,ω) будем обозначать сокращенноX (t) илиX .

Мы рассмотрим случайные процессы с действительными значениями.

При фиксированном значении X (t₀,ω) является случайной величиной, которая называетсясечениемслучайного процесса в момент времениt₀ .

При фиксированном значении X (t,ω₀) является неслучайной (обычной) функцией от времениt, которая называетсяреализацией случайного процесса.

2. Математическое ожидание с. п. При фиксированном значенииtсечениеX(t) является случайной величиной. Пусть для любогоtT существует математическое ожиданиеМ[X (t)].

Математическим ожиданиемс.п.X (t) называется неслучайная функция от времени t

m_X (t) =М[X (t)].

Свойства математического ожидания с. п.ПустьX(t),Y(t)случайные процессы,φ(t)неслучайная функция,Сконстанта.

1. m_φ (t) = φ (t).

2. m_X+Y (t) = m_X (t) + m_Y (t).

3. m_СХ (t) = С∙m_X (t).

4. m_X∙Y (t) = m_X (t)∙m_Y (t), если сеченияX (t),Y (t) некоррелированы при каждом .

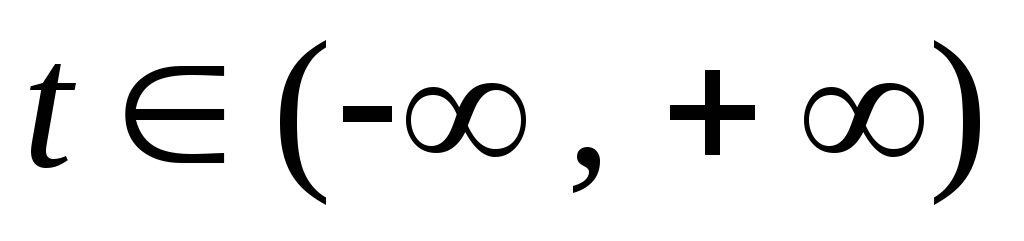5. m_φX (t) = φ (t)∙m_X (t).

3. Дисперсия с.п. Пусть при каждом фиксированномtдля сеченияX(t) определена дисперсияD[X(t)].

Дисперсией с.п. X(t) называется неслучайная функция от времениt

D_X (t)=D[X (t)].

Среднеквадратическим отклонением с.п. X(t) называется величина

Свойства дисперсии с.п. ПустьX(t),Y(t)случайные процессы,φ(t)неслучайная функция,Сконстанта.

1. D_X (t) ≥ 0.

2. D_φ (t) = 0.

3. D_φX (t) = (φ (t))²D_X (t).

4. D_φ+X (t) = D_X (t).

6. D_X+Y (t) = D_X (t) + D_Y (t), если сеченияX(t),Y(t) некоррелированы при каждом .