Пример 3.

Пусть mизвестно

Можно показать, что дисперсия такая же

S²=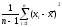, дисперсия этойS²

DS²=

Пусть Распределение Пуассона

P(X=k) =k=0,1,2…

I₁()======

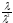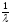
Получается дисперсия любой оценки DT>^/_n

Dx=^/_n, т.е. равенство достигается.

Билет №18.

Метод наименьших квадратов

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятности; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Линейная регрессия.

Модель:

Y₁,…,Y_n– независимые (некоррелированные) наблюдения

Пусть предполагается, что справедлива следующая модель .

- наблюдения (отклики),X’ –n*m–матрица (известны, характеризуют условия проверки эксперимента). Отклики линейно зависят от условий через параметр β. β – неизвестный параметр =.-ошибка (шумы).

Основные предположения:

а)

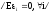
б)

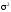- мешающий параметр – неизвестен.

В условиях (а), (б) EY=X’β.

Задача точечного оценивания – построить оценки параметра β при мешающем параметре .

Оценка по методу наименьших квадратов (МНК)

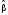
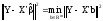, где норма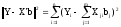

Примеры:

1) Измерительный прибор

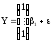/некор. О.Р.С.В./

Прямая на плоскости .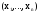- хар-ка процесса.

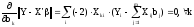
В матричной форме - нормальные уравнения. Еслиrk(XX^T)=m(т.е.rkX=m), то матрица будет обратимой, получаем-оценка по МНК.

Геометрическая интерпретация:

–i-я строка матрицыX’, то.

_.

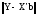_- столбец.-расстояние между элементамиYиX’b.

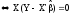
Вывод: решение существует.

Билет №19.

Оценки наименьших квадратов.

МНК-оценками, полученными по методу наименьших квадратов неизвестных параметров a и b в линейной регрессионной модели

Δ

Y_k = aX_k + b + W_k,

^

^

k = 1,n, называются оценки a(Zn) и b(Zn) ,

значения которых минимизируют квадратическую функцию Q(zn,a,b), построенную по апостериорной выборке zn.

Замечание 1. В данном случае видно, что функция Q(zn,a,b) совпадает по форме с точностью до коэффициентов с логарифмической функцией правдоподобия:

~

Q(zn,a,b) = -2σ²L(zn,a,b) -2σ²n ln(σ√2π).

Поэтому минимум функции Q(zn,a,b) по параметрам a и b достигается при тех же значениях

^

^

a и b ,

что и в методе максимального правдоподобия (минимизация функции Q(zn,a,b) по a и b эквивалентна максимизации функции L(zn,a,b)) и определяется соотношениями из примера Л15.Р2.П1.

~

^

^

Замечание 2. Найденные по методу наименьших квадратов оценки a(zn) и b(zn) неизвестных параметров a и b имеют место для произвольных случайных ошибок Wk и случайных коэффициентов Xk, тогда как по методу максимального правдоподобия эти же оценки получены в предположении о нормальности Wk и для детерминированных значений xk, k =1,n. Иными словами, МНК-оценки оказываются более робастными (т.е. менее чувствительными к априорной информации о случайных коэффициентах Xk и ошибках Wk) по сравнению с ММП-оценками.

Билет №20

Теорема Гаусса-Маркова.

Если матрица Х неколлинеарна и вектор случайных возмущений удовлетворяет следующим требованиям:

1.M(u) =0

2.σ²(u) = σ²_u

3.Cov(u_i,u_j) =0 при i≠j

4.Cov(x_i,u_i) =0

Тогда наилучшей линейной процедурой оценки параметров модели (8.1) является: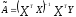

При этом: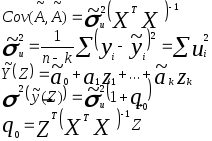

Пример 1. Пусть имеем выборку из nнаблюдений за случайной величинойY. Найти наилучшие оценки среднего значения и дисперсии этой переменной.

В терминах теоремы Гаусса –Маркова задача формулируется так: необходимо построить модель типа Y = a₀ +u, при этом имеем:

Решение.

.

Билет №22

Лемма Неймана-Пирсона.

Вводится 0<(x)<1,

Где (x) – вероятность отвержения гипотезы,

1-(x) - вероятность принять гипотезу.

Если (x) = 1, xW и

(x) = 0, xW, то критерий нерэндомизированный.