32) Примеры вывода полноты.

Свойство полноты. Полные статистики.

X, p(x,) – плотность, T – статистика

если из E_f(T(x))=0  => f(x)=0

Будем рассматривать полные достаточные статистики (ПДС), получим ограничение сверху и снизу.

Пример вывода полноты.

Если существует экспоненциальное распределение, то при определенных условиях T=(T₁,…,T_n) является полной статистикой.

Надо, чтобы в T_i_i(), _i было k-мерным, (₁()),…,_k()) отображалось в R^k.

1) Схема Бернулли

Предположим, что m – число успехов, является достаточной статистикой.

возьмем _m=0ⁿf(m)C_n^mp^mq^n-m=0  q(0,1), нужно доказать, что f(m)=0

_m=0ⁿf(m)C_n^mZ^m=0, Z=^p/_q, Z(0,)

получается полином с коэффициентами = 0, т.к. C_n^m0, то f(m)=0

2) Распределение Пуассона

Существует объем выборки n=1, тогда

=0  уберем e получим

=0, для >0 ¹/_k!0 => f(k)=0

2. Равномерное распределение R(0,)

объем выборки n=1

получается => f(x)=0с вероятностью 1

33) Доверительный интервал и примеры. Доверительный интервал.

Существует выборка x₁ x₂ … x_n с плотностью распределения P(x,) надо построить интервал с произвольными концами P_(())=1- надо выбрать интервал покороче.

Например

Хотим построить доверительный интервал дл m

² неизвестно

x – оценка для m

отцентрируем (x – m), тогда дисперсия будет /m

(отнормировали)

распределение Т мы знаем

=> =>

Примеры

² неизвестно

;

надо для t построить интервал

Если симметричен, то легко ограничить и получить маленький интервал

Можно брать по-разному, но сумма площадей хвостов= (т.е. 1/3 и 2/3)

Пусть /2

;

= >

доверительный интервал:

Рассмотрим схему Бернулли

выборка хотим построить доверительный интервал для Р

воспользуемся законом больших чисел:

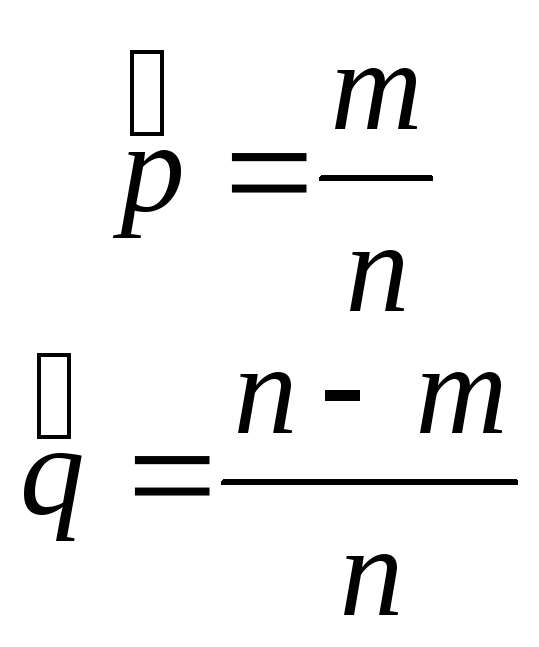
можно взять

=>

доверительный интервал:

Асимптотический доверительный интервал

Пусть n=2k+1

упорядочили

x_(k+1) – выборочная медиана

Выборочная медиана:

m

m совпадает с матожиданием

Какая оценка лучше?

x – лучшая оценка (x_(k+1) - хуже)

Выборочная медиана при нарушении основных предположений меняется мало, а x – сильно.

Пример

Пусть - плотность распределения Коши.

Характеристическая функция у x совпадает с характеристической функцией одного наблюдения (для Коши), т.е. информация о параметре в x такая же, как в одном наблюдении, т.е. x – несостоятельна. Ее нельзя применять, а - дает хорошую оценку.

Распределение Коши похоже на нормальное.

Сколько мы теряем, если распределение нормальное?

Построим доверительные интервалы. Какой короче?

1) По x :

2) По  :

, если x=, то

т.е. интервал для в больше, чем дляx. Это асимптотически больше для n.

34) Неравенство Рао-Крамера. Теорема Рао-Крамера

Пусть существует X=(X₁,...,X_n), g(), p(x,)

E_T=g(), для всех R.

D_T>-неравенство Крамера

Граница может достигаться а может и не достигаться

Всегда имеем дело с оценкой, насколько она хороша – она не может быть лучше дисперсии. Если она мало отличается от дисперсии, то оценка хорошая.

I()=,тогда неравенство Рао-Крамера выполняется, но оно выполняется не всегда, а при определенных условиях

Пример:

Условие регулярности

1. I() корректно определению, т.е. существует производная и такое мат.ожидание I() конечно

2. Можно переходить к пределу под знаком 

=-возможность дифференцирования под знаком интеграла, достаточно потребовать h(x) –рвномерно по всем 

h(x) – интегрируема в Rⁿ

если 1), 2) выполняются, то выполняется неравенство Рао-Крамера.

I(информационное количество Фишера

Доказательство:

Т.к. T – несмещенная оценка для g(), то E_T=g(), а E_+T=g(), значит g()-g()=E_+T-E_T=T(x)p(x,)d-T(x)p(x,)d=T(x)(p(x,)-p(x,))d(T(x)-ET(x))(p(x,)-p(x,))d= =применим неравенство Коши-Буняковского в терминах мат.ожидания

|Exy|<(Ex²Ey²) равенство <=> когда x,y пропорциональны с вероятностью 1, т.е. существует константа : x=y

<

Это верно при малых . Условие регулярности позволяет перейти к пределу 0

Случай равенства:

T(x)-E_T(x)=()

- это экспоненциальное семейство первого порядка

т.е. равенства достигаются, если p(x,) – экспоненциальное семейство, тогда T – ПДС

D_T>(g’())²/I()

I()=, p(x,)=

ln p(x,)=

=

=(*)

==0

достаточно, чтобы p(x,) мажорировалась непрерывной функцией. => (*)=0

тогда I()=nI₁()

I() – информация о всей выборке

I₁() – информация о первом наблюдении

D_T>(g’())²/nI₁() при условии регулярности дисперсия убывает не быстрее чем ¹/_n

Замечание:

Существует случай, когда дисперсия убывает быстрее чем ¹/_n