Лемма Неймана-Пирсона ( нерэндомизированный вариант).

В условиях поставленной задачи существует единственный (с точностью до множества нулевой вероятности) наиболее мощный критерий уровня значимости  и не зависящий от мощности.

Критическая область: W = {x: 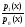>C}

Доказательство:

Докажем, что мощность всех других критериев с W₁ меньше мощности критерия с W:

(W)  (W₁).

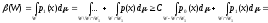
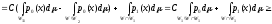
что и требовалось доказать.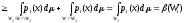

Лемма Неймана-Пирсона ( рэндомизированный вариант).

В условиях поставленной задачи существует единственный (с точностью до множества нулевой вероятности) наиболее мощный критерий уровня значимости  и не зависящий от мощности.

Данный критерий представляется в виде:

Доказательство:

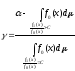
критерии зависит от уровня значимости и не зависит от мощности, что и требовалось доказать.

Билет №25

Критерии Стьюдента

Распределение t Стьюдента — это распределение случайной величины

,

где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределение N(0,1), а X — распределение хи-квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.

В настоящее время распределение Стьюдента — одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и так далее.

t-критерий Стьюдента- общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи примененияt-критерия связаны с проверкой равенства средних значений в двух выборках.Содержание [убрать]

Требования к данным:

Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.

Двухвыборочный t-критерий для независимых выборок

В случае с незначительно отличающимся размером выборки применяется упрощённая формула приближенных расчётов:

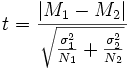
В случае, если размер выборки отличается значительно, применяется более сложная и точная формула:

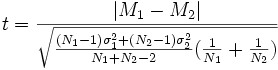
Где M1,M2 - средние арифметические,σ1,σ2 - стандартные отклонения, аN1,N2 - размеры выборок.

Количество степеней свободы рассчитывается как

Двухвыборочный t-критерий для зависимых выборок

Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:

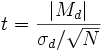
где Md- средняя разность значений, аσd- стандартное отклонение разностей.

Количество степеней свободы рассчитывается как

Одновыборочный t-критерий

Применяется для проверки гипотезы об отличии среднего значения от некоторого известного значения:

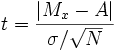
Количество степеней свободы рассчитывается как

Непараметрические аналоги

Аналогом двухвыборочного критерия для независимых выборок является U-критерий Манна-Уитни. Для ситуации с зависимыми выборками аналогами являются критерий знаков иT-критерий Вилкоксона

Билет №26

Сравнение двух выборочных дисперсий из нормальных совокупностей

Для определения того, относятся ли две выборки к одной и той же генеральной совокупности.

Проверяется гипотеза вида . Статистика для проверки гипотезы имеет вид

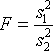. В случае принадлежности выборок нормальному закону и справедливостиэта статистика подчинятся -распределению Фишера с числом степеней свободыи(). В зависимости от альтернативы критерий может быть односторонним () или двусторонним (например,).

В многочисленных источниках подчеркивается, что результат проверки может сильно зависеть даже от небольших отклонений от нормального распределения.

Непараметрические критерии о дисперсиях: для сравниваемых рядов измерений образуют и к ним применяют критерий суммы рангов; если ряды абсолютных отклонений можно рассматривать как выборки из распределений с равными средними значениями, при двух выборках применяется U-критерий, при большем числе выборок H-критерий Краскела-Уоллиса.

Билет №27

Критериях согласия Колмогорова и Смирнова

В статистике критерий согласия Колмогорова (также известный, как критерий согласия Колмогорова-Смирнова) используется для того, чтобы определить, подчиняются ли дваэмпирических распределения одному закону, либо определить, подчиняется ли полученное распределение предполагаемой модели.