Неравенство Рао-Крамера. Теорема Рао-Крамера

Пусть существует X=(X₁,...,X_n), g(),p(x,)

E_T=g(), для всехR.

D_T>- неравенство Крамера

Граница может достигаться а может и не достигаться

Всегда имеем дело с оценкой, насколько она хороша – она не может быть лучше дисперсии. Если она мало отличается от дисперсии, то оценка хорошая.

I()=, тогда неравенство Рао-Крамера выполняется, но оно выполняется не всегда, а при определенных условиях

Пример:

Условие регулярности

1. I() корректно определению, т.е. существует производнаяи такое мат.ожиданиеI() конечно

2. Можно переходить к пределу под знаком 

=- возможность дифференцирования под знаком интеграла, достаточно потребоватьh(x) – рвномерно по всем

h(x) – интегрируема вRⁿ

если 1), 2) выполняются, то выполняется неравенство Рао-Крамера.

I(информационное количество Фишера

Доказательство:

Т.к. T– несмещенная оценка дляg(), тоE_T=g(), аE_+T=g(), значитg()-g()=E_+T-E_T=T(x)p(x,)d-T(x)p(x,)d=T(x)(p(x,)-p(x,))d(T(x)-ET(x))(p(x,)-p(x,))d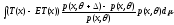==применим неравенство Коши-Буняковского в терминах мат.ожидания

|Exy|<(Ex²Ey²) равенство <=> когда x,y пропорциональны с вероятностью 1, т.е. существует константа: x=y

<

Это верно при малых . Условие регулярности позволяет перейти к пределу0

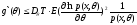
Случай равенства:

T(x)-E_T(x)=()

- это экспоненциальное семейство первого порядка

т.е. равенства достигаются, если p(x,) – экспоненциальное семейство, тогдаT– ПДС

D_T>(g’())²/I()

I()=, p(x,)=

ln p(x,)=

=

=(*)

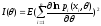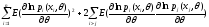
==0

достаточно, чтобы p(x,) мажорировалась непрерывной функцией. => (*)=0

тогда I()=nI₁()

I() – информация о всей выборке

I₁() – информация о первом наблюдении

D_T>(g’())²/nI₁() при условии регулярности дисперсия убывает не быстрее чем¹/_n

Замечание:

Существует случай, когда дисперсия убывает быстрее чем ¹/_n

Пример 1.

Пусть R(0,) – ПДС , статистикаT=max_i<nx_i, но она смещенная.

Пусть T₁=- несмещенная

D(T₁)=D_T=, нарушено условие регулярности для равномерного распределения, т.к. область зависит от, тогда нельзя говорить о дифференцируемостиp/

Т.е. такие распределения не очень хороши для оценивания

Такое явление, когда дисперсия убывает быстрее, чем ¹/_n, называется суперэффективным

Не всегда существует оценка : в неравенстве Рао-Крамера достигается равенство.

Рассмотрим ситуацию : D_>(g’())²/I()

но k-мерный=(₁,…,_k)

Будем понимать под g’() – градиент из частных производных.

g'()=)

под I() понимаем :I()=

I()=

i_m,n=, тогда дисперсияD_T>¹/_ng'()I^-1()(g'())^T

Пример 2.

N(m,²)

Пусть существует выборка из нормального распределения оценивать надо скалярные величины, будем оценивать m,²

Надо посчитать информацию матрицы Фишера

p(x,)=

ln p(x,)=

==

=====

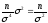
т.е.

i₁₂=i₂₁=E((=0, т.к. перемножаются либо 1, либо 3 моменты.

I=,I^-1=, т.е. по Неравенству Рао-Крамера

D_T>2²/n

g'()=(0,1)

D_T>g'()I^-1()g()/n

Всегда ли достигается равенство

Пусть существует эффективная оценка S²=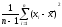

Посчитаем дисперсию оценки:

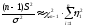
DS²=

Границы не совпадают

=> этом примере ни при каких nне достигается равенство в неравенстве Рао-Крамера

Если какой-то параметр знаем, то равенство достигается