32. Диференціальні рівняння з відокремленими змінними. Однорідні та лінійні диференціальні рівняння 1-го порядку.

Диф.р-ння 1-го порядку у (штрих)=f(х,у)наз.р-нням з відокремленими змінними., якщо його можна представити у вигляді у(штрих)=

= .

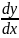Нехай ≠0, тоді .

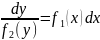Одержане р-ння наз.р-ння з відокремленими змінними.

Інтеграл .

Інтегруючи почленно це р-ння одержимо заг.розв»язок початкового р-ння.

При розв»язанні диф.р-нянь з відокремленими змінними потрібно:

*Відокремити змінні

*Про інтегрувати р-ння з відокремленими змінними, знайти його заг.розв»язок

*Знайти частинний розв»язок, що задов..поч.умови (якщо вони задані).

Однорідні диф.р-ння 1-го порядку.

Ф-ція f(x,у)наз. Однорідною ф-цією n-го степеня, якщо при будь-якому t(крім можливого t≠0) має місце тотожність f( , )=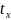

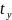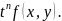
Диф.р-ння у(штрих)=f(х,у) наз.однорідним, якщо його можна представити у вигляді:

P(х,у)dx+Q(x,y)dy=0

P(х,у) і Q(х,у) – однорідні ф-ції одного й того самого степеня. Однорідне диф.р-ння зводиться до диф.р-ння з відокремлюваними змінними за допомогою підстановки у=U(штрих)х+U Лінійні диф.р-ння 1-го порядку у(штрих)=f(х,у) наз. Лінійним, якщо його можна представити у вигляді у’+Р(х)у=Q(х), де Р(х) і Q(х)-задані ф-ції від х, неперервні на деякому інтервалі .

Лінійне диф.р-ння зводиться до р-ння з відокремленими змінними за допомогою деякої підстановки у=UV, де одна із функцій U,V підбирається певним чином, а друга – нова невідома ф-ція.

33. Лінійні однорідні диференціальні рівняння 2-го порядку із сталими коефіцієнтами.

Лінійним – однорідним рівнянням ІІ порядку із сталими коефіцієнтами називається рівняння виду

y̕̕+py̕+qy=0 (1)

p I q – сталі величини

Для знаходження загального розв̕язку цього р-ня достатньо знайти два його частинні розв̕язки.

Будемо шукати частинні розв’язки у вигляді y = ? K = const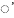 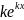y = y̕̕ =

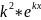
Підставляючи у̕ і у̕̕ у рівняння (1) одержимо:

+ р( ) + q = 0

( + pk + q) = 0

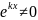+ pk + q = 0 це рівняння називається характеристичним рівнянням для рівняння (1).

Розв’язавши характеристичне р – ня знайдемо його корені 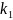I 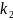, а отже і частинні розв’язки р – ня (1) = =

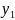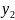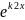
При розв’язку характ. р – ня можливі 3 випадки:

Корені характ. р – ня дійсні і різні ( ) тоді загальний р – ок р – ня матиме вигляд : y = * + *

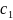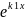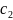Корені характ. р- ня дійсні і рівні ( )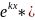

Корені характ. р – ня комплексні = а+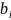 ; =a-

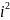=-1 загальний розв’язок: у= *( + )
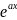