Геометричний зміст теореми Роля

Якщо ф-я задовольняє теореми Ролля то на графику цієї ф-ї знайдеться хоча б одна точка в якій дотична паралельна осі (ох)

19. Теорема Лагранджа

Якщо ф-ція f(x) неперервна на відрізку (а;b) і диференційована на інтервалі (а; b), то існує хоча б одна точка с з інтервала (а;b) така що 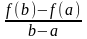=f̕(c)

Доведення:

Розглянемо допоміжну ф-цію γ(x)

F(x)= f(x) *(x-a)

Ця ф-ція задовольняє всі умови теореми Ролля:

Вона не перервна на відрізку (а;b), як різниця двох неперервних ф-цій. F(x) і *(x-a), Вона диференційована в інтервалі (а;b) при чому γ̕(х)= f̕(x)- , На кінцях відрізка (а;b) ф-ція γ(x) має однакові значення

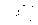γ(b)= *(b-a)=f(a)=γ(a), Тоді за теоремою Ролля існує хоча б одна точка с з інтервала (а;b) в якій γ̕(с)=0, В похідну допоміжної ф-ції підставимо значення х=с, 0=f̕(c)- , = f̕(c)

Геометричний зміст

Якщо ф-ція F(x) задовольняє умови теореми Лагранджа, то серед усіх дотичних до кривої y=f(x) знайдеться хоча б одна яка паралельна хорді АВ що з’єднує кінці дуги ф-ції f(x) на відрізку (а;b)

20. Теорема Коші

Якщо ф-ція f(x) і γ(х) неперервні на відрізку (а;b) і диференційовані в інтервалі (а;b) при чому γ̕(х)≠0 в усіх точках інтервалу (а;b), то існує хоча б одна точка с з нтервала (а;b), така що =

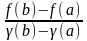Доведення:

За теоремою Лагранджа умови якої тут виконуються, маємо γ(b) – γ(a) = γ̕(c)*(b-a). Оскільки γ̕(с)≠0, то γ(b)≠ γ(a), введемо допоміжну ф-цію ψ(х)= *(х-а)

ψ(х)= f(x) - *(γ(х)-γ(а))

Ця ф-ція задовольняє всі умови Ролля:

Вона не перервна на відрізку (а;b)

Диференційована в інтервалі (а;b) при чому для всіх х з інтервала (а;b)

Ψ̕(х) = f̕(x) - * γ̕(х)

На кінцях відрізка (а;b) ф-ція Ψ(х) має однакові значення:

Ψ(b) = f(b) - * (γ̕(b) - γ(а))= f(a)

Ψ(a) = f(a)

За теоремою Ролля існує хоча б одна точка с з інтервала (а;b) в якій ψ̕(с) =0. Підставляємо у похідну замість х=с

0= f̕(c) - * γ̕(c)

* γ̕(c) = f̕(c)

=

21. Основні поняття та означення функції багатьох змінних. Частинні похідні та повний диференціал 1-го порядку.

1 приклад. Площа S прямокутника зі сторонами, довжини яких дор.х та у вир.формулоюS= ху. Кожній парі чисел х та у відповідає певне значення площ і S .S є функцією двох змінних.

2 приклад. Об»єм V прям.паралелепіпеда з ребрами, довжини яких дор.х,у,z вир.ф-лою:V=xyz.Тут V є функцією 3-х змінних.

3 приклад.U= . Функція U є функцією 4-х змінних.

Ф-ція 2-х змінних (х,у) наз.залежність при якій кожній парі чисел х,у ставиться у відповідність деяке число f(x,у).

Частинною похідною по х від ф-ції Z(х,у) наз.границя відношення частинного приросту ∆Х при умові, що дельта х→0.

Частинною похідною по у від ф-ції Z=f(x,у)наз.границя відношення частинного приросту ф-ції 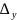Z до приросту дельта у при умові, що ∆ у→0.

Повний приріст ф-ції Z=f(х,у) обчислюють за ф-ло.

∆z=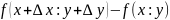

Повний диференціал

Нехай ф-ція Z=f(х,у) має неперервні частинні похідні і диференційована в т.(х,у), то її повний диференціал дор.сумі добутків частинних похідних на диференціали відповідних незалежних змінних:

dz= *dx+