4. Розв'язування систем лінійних рівнянь за формулами Крамера.

Нехай задано систему трьох лінійних рівнянь з трьома невідомими.

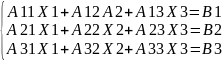(1)

Аіj (i=1,2,3 j=1,2,3) – коефіцієнти при невідомих

Х1,Х2,Х3 – невідомі

В1,В2,В3 – вільні члени

Розвязком системи 1 називаеться будь-яка сукупність значень невідомих Х1=С1, Х2=С2, Х3=С3

Підстановка яких в кожне рівняння системи перетворює ці рівняння в тотожність.

Якщо визначник системи ∆ відмінний від нуля, то система має один розвязок, який знаходиться за формулою Крамера.

Х1 =

Х2 =

Х3 =

Де ∆Х1, ∆Х2, ∆Х3 – це визначники третього порядку, одержаний із визначника системи, шляхом заміни відповідно першого, другого і третього стовпців, стовпцями із вільних членів системи.

Якщо визначник системи ∆=0, а серед визначників ∆Хі (і = 1,2,3) хоча б один відмінний від нуля, то система не має розвязків.

Якщо ∆ = ∆Х1 = ∆Х2 = ∆Х3 то система має безліч розвязків.

Система лінійних рівнянь для якої В1 = В2 = В3 =0 назив.лінійною однорідною системою рівнянь.

5.Загальне рівняння прямої та його частинні випадки.

- загальне рівняння прямої.

Нехай , тоді (ця пряма буде паралельна осі ОХ).

Якщо , то - пряма,що визначає вісь ОХ.

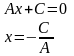
Нехай , тоді (ця пряма буде паралельна осі ОУ).

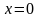Якщо , то - пряма,що визначає вісь ОУ.

Нехай 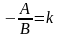, тоді - пряма буде проходити через початок координат.

Нехай , а , тоді - рівняння прямої з кутовим коефіцієнтом і початковою ординатою.

6. Різні види рівнянь прямої на площині.

Прямі на площині в декартових координатах можуть бути задані такими рівняннями:

- загальне рівняння прямої

- рівняння прямої,що проходить через дану точку із заданим нормальним вектором.

- нормальний вектор, - координати даної точки.

Будь-який ненульовий вектор,перпендикулярний до даної прямої,називається нормальним вектором цієї прямої.

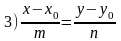- рівняння прямої,що проходить через дану точку із заданим напрямним вектором(канонічне рівняння прямої).

-напрямний вектор.

Будь-який ненульовий вектор,паралельний до даної прямої,називається напрямним вектором цієї прямої.

, - параметричне рівняння прямої,де t-параметр.

- рівняння прямої,що проходить через дві задані точки.

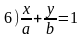- рівняння прямої у відрізках.

відрізки,що їх відтинає пряма на координатних осях ОХ та ОУ.

- рівняння прямої з кутовим коефіцієнтом і початковою ординатою.

Кутовий коефіцієнт прямої дорівнює тангенсу кута нахилу цієї прямої до додатного напряму осі ОХ.

, -величина відрізка,що відтинається прямою на осі ОУ.

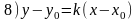- рівняння прямої,що проходить через дану точку із заданим кутовим коефіцієнтом.

7. Лінії 2-го порядку, загальне рівняння.Коло та його рівняння.

Алгебраїчним рівнянням другого степеня називається рівняння виду (1), де A,B,C,D,E,F-дійсні числа,і хоча б одне із чисел . В протилежному випадку рівняння (1) не буде рівнянням другого степеня.

Лінії,які в декартовій системі координат визначаються алгебраїчним рівнянням другого степеня, називаються лініями другого порядку(кривими другого порядку).

Розглянемо 4 лінії другого порядку:коло,еліпс,гіпербола,парабола.

Коло та його рівняння.

Коло – множина всіх точок площини рівновіддалених від даної точки,яка називається центром кола.

Рівняння кола,з центром в точці і радіусом r,має вигляд: (2)

- рівняння кола,центр якого знаходиться на осі ОХ.

- рівняння кола,центр якого знаходиться на осі ОУ.

- рівняння кола,з центром у початку координат.

Рівняння (2) є частинним випадком загального рівняння другого степеня із змінними Х,У. Розкривши дужки в рівнянні (2) одержимо:

, де

Загальне рівняння ліній другого порядку буде визначати коло,якщо:

, ,

8. Еліпс та його канонічне рівняння.

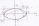Еліпсом назив.площина всіх точок площини,сума відстаней від кожної із яких, до двох даних точок цієї площини,які.назив. фокусами,є величина стала і більша ніж відстань між фокусами. 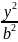_{+ =1-} канонічне рівняння еліпса (1)

_{- =} F:2 Є Ох

_{- =} F:2 є Оу

А1А2=2а а-велика піввісь

В1В2=2в в-мала піввісь

_{О- центр} еліпса та центр симетрії еліпса

2с-фокусна відстань А1,А2,В1,В2-вершини еліпса,їх чотири

Вивчення форми еліпса за його канонічним рівнянням:

1)Координати точко О(о;о) не задовольняють канонічне рівняння еліпса, тому еліпс не проходить через початок координат.

2)Знайдемо точки перетину еліпса з осями координат

Ох:у=0, тоді 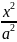=1 => - =>х= точки перетину еліпса з віссю ох:А1=(а;0) А2(-а;0) ; Оу:=0=> =1

= у=

Еліпс перитинає вісь оу: В1(0;в), В(о;-в)

3)Так як в рівнянні (1) змінні х та у входять тільки в парних степенях, то еліпс семитричний відносно осей координат, а отже відносно початку координат.

4)Знайдемочастини площини в якій розміщено еліпс:

|у| в

-а -в

Всі точки еліпса знаходяться в середині прямокутника зі сторонами х=а, х=-а, у=в,у=-в

Ексцентриситетом еліпса назив. Відношення відстані між фокусами , до довжини великої осі.

Е=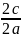 = =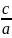 *(а>в) F1:2 є Ох

Е= = = *(а<в) F1:2 є Оу

За величину ексцентриситета можна судити про форму еліпса.Чим більший ексцентр. Тим більше витягнутий елінс, чим менший ексциетр.тим кругліший еліпс. Якщо а=в, то Е=0 і рівняння еліпса матиме вигляд + = (коло). Коло можна розглядати, як частинний випадок еліпса, у якого півосі рівні між собою, а отже ексцинтр.=0, Е=0.

9. Гіпербола, її канонічне рівняння.

Гіперболою назив.множина точок площини, модуль різниці відстані від кожної з яких, до двох даних точок тієї ж площини, які назив.фокусами,є велчина стала і менша ніж відстань між фокусами.

F1F2=2c-фокусна відстань

F1(c;0) F2(-c;0), Нехай М(х;у) довільна точка гіперболи, F1M=r1-фокальні радіуси точки М

F2M=r2,О- центр симетрії гіперболи, - =1-(1)

,А1А2=2а-дійсна вісь гіперболи,В1В2=2в-уявна вісь гіперболи

а-дійсна вісь,в-уявна вісь

Властивості гіперболи:

1)Точка О(о;о) не задовольняє рівняння(1), тому гіпербола визначена цим рівняннями, не проходить через початок координат.

2)Знаходимо точки перетину гіперболи з осями координат:Ох:у=0=> , ,х=

Гіпербола має дві точки перетину з віссю ох:А1(а;0);А2(-а;о)-вершини гіперболи.

Оу:х=0 , 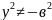Гіпербола не має точок перетину з віссю оу(ординат).

3)Так як змінні х та у входять в рівняння(1) парних степенях, то гіпербола симетрична відносно осей координат,а отже відносно початку координат .

4)Якщо х прямує до + , то у змінюється(прямує) до , якщо х прямує до - .

Прямі у= х назив.асимптотами гіперболи.

Ексцинтреситетом гіперболи назив.відношення відстані між фокусами до довжини дійсної осі.

Е=

Ексцинтр.гіперболи більше 1. Гіпербола назив.рівньосторонььою,якщо довжини півосей рівні між собою, тобто а=в, тоді рівняння рвньостороньої гіперболи матиме вигляд

Е=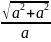 = = = Ексцинтреситет всіх ріносторонніх гіпербол=

1 0.Парабола та її канонічне р-ня:Параболою назив.множина точок площини,кожна із яких рівновіддалена від даної точки, що назив. Фокусом і від даної прямої, що не проходить через дану т. і назив директрисою.

Відстань від фокуса F до директриси d назив. Параметром параболи і познач-p(р>0)

F(p/2;0)

x= - p/2 ­ р-ня директриси

M(x;y)-довільна точка параболи(NM=FM)

y²=2px-канонічне р-ня параболи з фокусом F(p/2;0)

Властивості параболи:

1.Т.О(0;0) задовольняє р-ня параболи тому парабола визначена цим р-ням проходить через початок координат.

2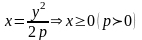 .Т.я. змінна y в р-ні параболи в парному степені то парабола симетрична відносно осі ОХ

3.З р-ня параболи виразимо х:

Парабола у²=bx розміщена праворуч від осі ОУ

При зростанні х від 0 до +∞, у змінюється від 0 до ∞,тобто, точки нескінченного віддаляються,як від осі ОХ так від осі ОУ

Якщо фокус параболи розміщений ліворуч від осі ОУ, а директриса-праворуч від неї,то втіки параболи розміщені ліворуч від осі ОУ

Р-ня такої параболи має вигляд: y²= - 2рх, F(-p/2;0); x=p/2 – р-ня директриси

Якщо F(0;р/2), р-ня директриси- у= - р/2, то р-ня параболи матиме вигляд х²=2ру

Вітки цієї параболи напрямлені вгору.

Якщо F(0; - р/2)

У =р/2, то р-ня параболи матиме вигляд: х² = - 2ру

Вітки цієї параболи напрямлені вниз

№11 Нескінченно великі та нескінченно малі величини, зв'язок між ними. Властивості нескінченно малих величин.

Якщо змінна х прямує до нескінченності то її називають нескінченно великою змінною величиною.

Нескінченно малою величиною називають змінна величина границя якої =0.

Зокрема функція α(х) –називається нескінченно малою величиною при або якщо ( )=0, або (х) =0.

Власттивості нескінченно малих величин:

1) Для того щоб число А було границею функції f(x) при необхідно і достатньо щоб різниця f(x) - А була нескінченно малою величиною, тобто

f ( )=А f(x) =А+ (x), де ( )=0

2) Якщо функція f ( ) нескінченно мала величина при то функція є скінченно великою величиною при , і навпаки якщо функція є нескінченно великою величиною при то є нескінченно малою величиною.

3) Сума скінченної кількості нескінченно малих величин є величина нескінченно мала.

4) Добуток обмеженої функції на нескінченно малу є величина нескінченно мала.

5) Частка від ділення нескінченно малої величини на функцію яка має відмінну від нуля границю є величина нескінченно мала.

12.Границя функції.Основні теореми про границі.

Властивості границь:

1)Границя суми(різниці) двох неперервних ф-цій=сумі(різниці) границь цих функцій

2)Границя добутку 2-ох неперервних ф-цій

3)Границя частки 2-х неперервних ф-цій=частці границь цих ф-цій при умові,що границя значення ≠0

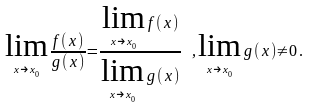
4)Сталий множник можна винести за знак границі

5)Функція не може мати в одній точці дві різні границі

6)Границя сталої величини дорівнює цій сталій:

13. Перша і друга визначні граниш. Розкриття невизначеностей.

Границя виду називається першою визначеною границею.

При застосуванні границь, що повязані з першою визначною границею. Використовуючи такі нескінченно малі еквівалентні величини.

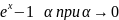
Границя виду

При обчисленні границь повязаних з числом е часто застосовують таке твердження:

Якщо існують границі

14. Неперервність функцій. Властивості неперервних функцій. Точки розриву.

Ф-ція буде неперервною в т. при умові:

А.ф-ція визначена в т. і в точці і в деякому околі цієї точки;

Б.існує границя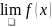

В.границя ф-ції в т. і значення ф-ції в цій т. збігаються,тобто викон.рівність:

Ф-ція буде неперервною в т. тоді і тільки тоді,коли вона визначається в деякому околі т. і

Якщо хоча б одна з умов не виконується,то ф-ція назив.розривною в т. ,а сама т. -точкою розриву ф-ції.

Розрізняють 2 види розривів:

А.якщо для ф-ції існують скінчені границі,то

при чому не всі числа рівні між собою ,то в т. ф-ція матиме розрив перого роду ,а точку назив.точкою розриву першого роду.

Величину називають стрибком ф-ції.

Б.якщо хоча б одна із сторонніх границь не існує або= ,то розрив в т. назив.розривом другого роду, а сама т. –точкою розриву 2-го роду.