22. Частинні похідні вищих порядків. Екстремуми ф-ії багатьох змінних

Частинними похідними 2-го порядку ф-ії z=f (x;y) наз. їх частинні похідні від частинних похідних першого порядку. Частинні похідні 2-го порядку від ф-ії 2-х змінних, так як кожну із ф-ії де: 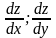можна диференціювати, я по х та і по у.

Частинні похідні, які відрізняються одна від одної лише порядком диференціювання наз. мішаними похідними.

Теорема Шварца!

Якщо мішані частинні похідні неперервні в деякому околі т. М то вони рівні між собою:

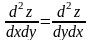,Диференціал 2-го порядку обчислюється за формулою: Ф-ія z=f (x;y) має max в т. М0 (Х0;У0), якщо f (X0;Y0) > f (x;y) для всіх точок х0;у0 і відмінних від неї.

Ф-ія z=f (x;y) має min в т. М0 (Х0;У0), якщо f (X0;Y0) < f (x;y) для всіх т. х;у достатньо близьких до т. х0;у0 і відмінних від неї.

Min і maх ф-ії 2-х змінних наз. екстремум ф-її.

Необхідна умова існування екстремуму: якщо ф-ія z=f(x;y) досягає екстремуму в т. х0;у0 то кожна частинна похідна першого порядку від цієї ф-ії = 0 або не існує при цих значеннях аргумента (х0;у0)

Критичні точки:

Точка в яких частинні похідні першого порядку = 0 або не існують наз. критичними точками ф-ії z=f(x0;y0)

Достатня умова існування екстремуму:

Нехай в деякій області, що містить т. М0 (х0;у0) ф-ія z=f(x;y) має неперервні частинні похідні до 3-го порядку включно і нехай крім того т. М0 (х0;у0) є критичною точкою ф-ії z=f(x;y)

1 . якщо АС-В2 >0 і А<0 то (х0;у0) є т. max.

2 якщо АС-В2 >0 і А>0 то (х0;у0) є т. min

3. якщо АС-В2 <0 то (х0;у0) не є т. екстремуму

4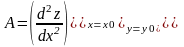 . якщо АС-В2 =0 то (х0;у0) може бути т. екстремуму, а може не бути (потрібне додаткове дослідження)

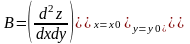
24 Метод інтегрування заміною змінної.

.Нехай функція f(x) неперервна і потрібно знайти

∫f(x)dx причому безпосоредньо важко підібр.таку ф-ю F(x),що ∫f(x)dx=F(x)+c.Зробимо заміну змінну інтергування х за ф-ю x=ϕ(t),де ф-я ϕ(t) монотонна і має неперервну похідну застосувавши y0 шуканої ф-ї F(ϕ(t))´,формулу диференц.складеної ф-ї одержимо (F(ϕ(t)))=f(ϕ(t))*ϕ´(t)

Так як ф-я f=ϕ(t),неперервна як складена ф-я ,а ϕ´(t) неперервна за умовою то одержимо рівність (∫f(ϕ(t))ϕ´(t)dt=F(ϕ(t))+c

В одержаній формулі необхідно знову перейти до змінної х.

25 Інтегрування частинами.

Нехай ф-ції u=u(x) v=v(x) мають неперервні похідні на деякому інтервалі.

Знайдео диференціал добутку цих функцій

D(uv)=u`v(dx)+v`udx

Так як за умовою функції і неперервні то можна про інтегрувати обидві частини

∫d(uv)=∫u`vdx+∫v`udx

∫d(uv)=uv+c

Uv=∫vdu+∫udv

∫udv=uv-∫vdu ---Формула інтегрування частинами

U`=du

Dv=v`

В iнтегралах виду ∫P(x)*e^axdx, ∫P(x)*sin(ax)dx, ∫P(x)*cos(ax)dx

Многочлен вiдносно х, а-деяке число приймають u=P(x)

В iнтегралах виду ∫P(x)*ln(ax)dx, ∫P(x)*arcsin(x)dx arcos, arctg, arcctg

Многочлен вiдносно х, а-деяке число приймають dv=P(x)

27.Означення визначеного інтеграла. Інтегральні суми. Властивості визначеного інтеграла,його геометричний зміст.

Нехай дана неперервна функція 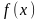на відрізку 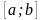і нехай функція на вказаному відрізку невід’ємна.

Виконаємо наступні операції:

1)розіб’ємо відрізок на 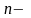частин так,що

2)позначимо . Величину 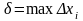називають кроком або діаметром розбиття.

3)в кожному із відрізків 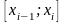зафіксуємо довільну точку

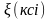
4)складемо суму 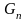всіх добутків або в скороченому вигляді (1).

С уму виду (1) називають інтегральною сумою функції .

Геометрично кожен доданок інтегральної суми дорівнює площі прямокутника з основою і з висотою , а вся інтегральна сума дорівнює площі «ступінчастої фігури», яка одержується об’єднанням всіх,вище вказаних,прямокутників.

Очевидно,що при всіх можливих розбиттях відрізка на частини, одержимо різні інтегральні суми виду (1) і різні ступінчасті фігури.

Таким чином,для даної функції і даного відрізка можна скласти нескінченну множину інтегральних сум,які залежать від вибору точок поділу 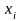і точок .

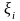Якщо при будь-яких розбиттях відрізка таких,що 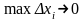і при будь-якому виборі точок ,інтегральна сума прямує до однієї і тієї ж скінченної границі A, то число A називають визначеним інтегралом від функції на відрізку і позначається .

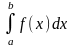Згідно означення,якщ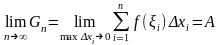о , то 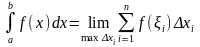Геометричний зміст визначеного інтеграла: Якщо функція f(x) неперервна і невід’ємна на відрізку [a;b], то визначений інтеграл чисельно дорівнює площі криволінійної трапеції,обмеженої графіком функції f(x), віссю ОХ і прямими x=a, x=b, .

Властивості визначеного інтеграла:

1)Інтеграл від суми двох неперервних функцій дорівнює сумі інтегралів від цих функцій:

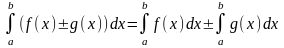
2)Сталий множник можна виносити за знак визначеного інтеграла:

,

3)Якщо , то:

4)Якщо функція 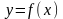невід’ємна на відрізку ,то:

5)Якщо

6)Теорема про середнє: Існує така точка С з відрізка [a;b],для якої виконується умова:

7)Інтеграл з однаковими межами дорівнює нулю:

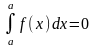
8)При зміні меж інтегрування,знак інтеграла змінюється на протилежний:

9)Якщо m і M - найменше і найбільше значення функції на відрізку ,то

28.Інтеграл із змінною верхньою межею. Теорема Ньютона-Лейбніца

Теорема 1

Якщо функція неперервна на відрізку і 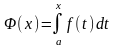,то або . Похідна від інтеграла із змінною верхньою межею дорівнює підінтегральній функції,в якій зміна інтегрування замінена цією межею. Це означає,що визначений інтеграл із змінною верхньою межею є однією із первісних підінтегральної функції.

Теорема 2.

Якщо функція неперервна на відрізку , а 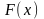є будь-якою її первісною на цьому відрізку,то

Доведення:

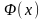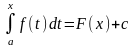Із теореми 1 випливає,що є теж первісною для функції на відрізку . Так як і дві первісні для однієї і тієї ж функції ,то або (2)

При х=а маємо:

0=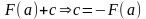

Підставимо значення в рівність (2),одержимо:

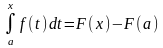
Нехай х=в,тоді:

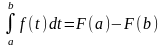
Позначивши зміну інтегрування буквою Х,одержимо формулу Ньютона-Лейбніца:

31. Диференціальні рівняння 1-го порядку. Основні поняття та означення. Теорема про єдиність та існування розв'язків. Задача Коші.

Диференціальним рівнянням 1-го порядку наз.р-ння, що містить незалежну змінну х, шукану ф-цію у та її похідну у.

Диф.р-ння 1-го порядку в загальному вигляді вигляді записується так: F(х,у,у)=0 (1)

Рівняння (1) може не містити явну х або у, але обов”язково має містити похідну у (в протилежному випадку воно не буде диф.р-нням).

Якщо р-ння (1) можна розв»язати відносно похідної х, то його записують у вигл.: у(штрих)=f(x,у) (2) і наз. р-нням 1-го порядку, розв»язаним відносно похідної.

Р-ння (2) можна записати: =f(x,у) або f(x,у)dx=dy.

Порядком диф.р-ння наз. Найвищий порядок похідної, що входить в дане р-ння.

Розв»язком диф.р-ння на деякому інтервалі наз. диференційована на цьому інтервалі ф-ція у=фи(х), яка перетворює дане р-ння в тотожність.

Теорема Коші (про єдність та існування розв»язків).

Нехай ф-ція f(х,у) та її частинна похідна по у визначені і неперервні у відкритій області G площини оху і точка , належить області G. Тоді існує єдиний розв»язок у=фи(х) диф.р-ння, який задовольняє умову: =фи( ).

Ця теорема дає достатні умови існування єдиного розв»язку диф.р-ння.