15 Означення похідної, її геометричний та фізичний зміст. Залежність між неперервністю та диференційованістю функцій.
Похідною
ф-ї f(x) в т. назив. границя відношення
приросту ф-ї
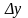до приросту аргумента
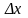при умові що
, якщо ця границя існує і позначається
.
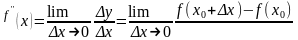Геометричний
зміст похідної
Нехай
неперервна ф-я у=f(x), х[а, в] диференційована
в т
і нехай L графік цієї ф-ї. на прямій L
візьмемо т
і т M(x y)і проведемо січну
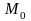Дотичною
до кривої L в т
наз пряма
T
що займає граничне положення січної
M
при
(якщо пол. існує)
Нехай
відповідно
кути нахилу дотичної
T
і січної
M
до додатн напрямку осі о(х)
З
малюнка видно що tg
Перейшовши до границі при
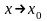одержимо
=
,
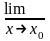
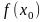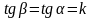(кутовий
коефіцієнт дотичної до кривої),
Похідною ф-ї а(х) в т
кутовому
коефіцієнту дотичної проведеної до
графіка даної ф-ї в його точці з абсцисою
Фізичний зміст
Нехай
матеріальна т рухається прямолінійно
за законом S=S(t) тоді похідна від шляху
по часу є миттєвою швидкістю прямолінійного
руху матеріал. т в будь-якой момент часу
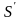V(t)=
(t)
Друга похідна від Sпо t, або перша похідна від швид по t є прискоренням матеріальної точки
a(t)=
(t)
або a(t)=
(t)
№17 Означення диференціалу функції. Правила знаходження диференціала.
Відомо щощо функція у=f(x), яка визначена на інтервалі [a;b] і деференційована в точці х нульове з інтервалом [a;b] то її приріст в цій точці може бути представлений у вигляді
∆ƒ(
,
α (∆χ) нескінченномала величина більш
вищого порядку ніж нескін.мала величина
∆χ.
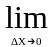
,Тому
говорять що величина
(
)
∆χ складає головну частину приросту
функції f(x) в точці ікс нульове.
Деференціалом функції у=f(x) в точці ікс нульове називається лінійна відносно ∆χ функція ( ) ∆χ що складає основну частину приросту функції в точці ікс нульове.
Позначається df(x) або dy
df(x)= (x)*∆x. ∆x≈dx
df(x)= (x)*dx
dy=y`dx
18. Теорема Ферма і Ролля.
Теорема
Ферма.Нехай
ф-я f(x) неперервна на інтервалі(а,в) і
набуває свого найбільшого або найменшого
значення у деякій точці с цього
інтервалу.Тоді якщо існує похідна то
вона=0 тобто f`(c)=0.
Геометричний зміст теореми Ферма.
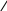
Дотична
до графіка ф-ї у=f(x) в точці що задовольняє
умови теореми Ферма паралельна осі
абсцис.
Теорема
Роля.
Якщо ф-я f(x) неперервна на відрізку(а,в)
диференційована в інтервалі (а,в) і на
кінцях відрізках набуває кінцевих
значень f(a)=f(b), то знайдеться хоча б одна
точка с з інтервалу (а,в), в якій похідна
=0 ,тобто f(c)=0
Доведення
Оскільки
ф-я f(x) неперервна на відрізку (а,в),то
вона досягае на цьому відрізку свого
найбільшого значення М,і найменшого
значення м.Якщо М=м,то f(x)=const ,і f`(x)=0,
в кожній точці х відрізка (а,в).Нехай
М≠м, тоді хоча б одне із значень М чи м
досягаеться функціею у внутрішній
точці інтервалу (а,в) тому f(a)=f(b),
тоді за теоремою Ферма похідна в такій
точці
=о