21. Теорема умножения вероятностей независимых событий.

Р(А и В)=Р(АВ)=Р(А)хР(В)

Произведением события А и В будет событие С=АВ состоящие из например попадания в мешен двух стрелков.

Произведение несовместных событий невозможно.

22. Условная вероятность. Теорема умножения вероятностей зависимых событий.  Условная вероятность- вероятность появления события А при условии что произошло событие В. Вероятность произведений событий обычно вычисляется по формуле

Р(А и В)=Р(А)х Р­А(В­) =Р (В)х Р ­В(А)

Для зависимых событий

Р(АиВ)=Р(А)х Р­А(В­)=Р(В)х Р ­В(А)

23. Теорема сложения вероятностей совместных событий

Теорема совместных событий- значит попадание хотя бы одного из испытыемых(может больше) рассчитывается по формуле

Р(А или В)=Р(А)+Р(В)-Р(АВ)

24. Формула полной вероятности.

События H1, H2, …, Hn образуют полную группу событий, если они попарно несовместимы и вместе образуют достоверное событие.

Теорема. Если события H1, H2, …, Hn образуют полную группу, а событие A происходит в результате появления одного и только одного из событий Hi, то используется формула:

Р(А)=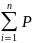 (Н­I­)Р­(A/Hi) (Н­I­)=1

H­I= ­Это выбор i (урны к примеру)

25. Теорема Байеса.

Определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях

Т. Пусть рассматриваются Н1,Н2…Нn – гипотезы образующие полную группу и событие А которое может наступить если произойдет одно из событий Hi тогда условные вероятности гипотез можно вычислить по формуле P(A/B)= P(B/A)P(A)/P(B)

26. Повторение испытаний (схема Бернулли). Формула Бернулли

Проводится множество испытаний независимых друг от друга.

Примеры повторных испытаний:

многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях).

m m n-m

Р­­­m,n­=C p q

n

Где n - –количество независимых испытаний

m – появление события А

р - вероятность события

q- не событие р

27. Дискретные и непрерывные случайные величины(определения, примеры). Функция распределения

Случайная величина- это переменная величина, конкретное значение которой зависит от случая .

Непрерывную случайную величину А следует задавать не указанием вероятностей ее отделных значений, а неприрывной функцией, называемой плотностью распределения вероятностей случайной величины А. непрерывная величина- величина постоянная. Для нее плотность распределения - максимум

Случайная величина называется дискретной, если множество ее значений конечно или счетно. Например- количество солнечных дней в году. Число опрошенных на занятии. Законом распределения ДСВ. Называют таблицу из двух строк. В верхней- значения. В нижней- вероятности этих значений. Следует заметит что .

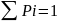Ф-ция распределения случайных величин 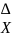называется функция действительного аргумента x равная вероятности того, что случайная величина примет значение меньше чем x. F(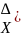 = P( X)