
- •1.Роль и место математики в современной науке.
- •6.Действия с множествами. Свойства действий.
- •9.Постоянные и переменные величины. Предел.
- •10.Бесконечно малые и бесконечно большие величины.
- •11. Производная функции: определение, геометрический и физический смысл.
- •13. Приложения производной (на примере).
- •14. Элементы логики. Алгебра логики.
- •16. Предмет и задачи теории вероятности. Области применения методов теории вероятностей.
- •17. Основные элементы теории вероятностей. Случайные события: понятия, виды случайных событий.
- •18. Вероятность случайного события: определение, способы вычисления вероятности.
- •19. Теорема сложения несовместных событий.
- •21. Теорема умножения вероятностей независимых событий.
- •27. Дискретные и непрерывные случайные величины(определения, примеры). Функция распределения
- •28. Характеристики распределения случайной величины.
28. Характеристики распределения случайной величины.
СВОЙСТВА:
Функция
распределения является ограниченной
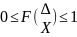
Функция распределения является неубывающей или постоянной.
Предел функции распределения при х стремится к

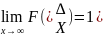
Вероятность попадания случайных величин в полуинтервал ав= разноси значений.
29. Законы распределения вероятностей дискретной случайной величины. Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
30. Законы распределения вероятностей непрерывной случайной величины. Плотность вероятности непрерывной случайной величины, она же дифференциальная функция распределения вероятностей - аналог закона распределения дискретной с.в. Но если закон распределения дискретной с.в. графически изображается в виде точек, соединённых для наглядности ломаной линией (многоугольник распределения), то плотность вероятностей графически представляет собой непрерывную гладкую линию (или кусочно-гладкую, если на разных отрезках задаётся разными функциями). Аналитически задаётся формулой. Если закон распределения дискретной с.в. ставит каждому значению x в соответствие определённую вероятность, то про плотность распределения такого сказать нельзя. Для непрерывных с.в. можно найти только вероятность попадания в какой-либо интервал. Считается, что для каждого отдельного (одиночного) значения непрерывной с.в. вероятность равна нулю. И графически вероятность попадания в интервал выражается площадью фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом. Свойства плотности вероятности: 1) Значения функции неотрицательны, т.е. f(x)≥0 2) Основное свойство плотности вероятности: несобственный интеграл от плотности вероятности в пределах от -∞ до +∞ равен единице (геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1)
31. Первичная обработка р-ов экспиримента. Этапы статистич-х данных: 1. Сбор 2. Систематизация 3. Анализ данных. Ген совокупнлсть – совокупность явлений, из которых производится выборка. Пусть из ген совокупности произведена выборка объемом n. Х1 – встреч-ся n1 раз, Х2 – встреч-ся n2 раз и т д. При этом n1+n+…nk = n Xi – варианты ni – частоты. Вариационный ряд – таблица. График – y – ni, x-xi.
32. Выборочный метод мат статистики. Ген совокупность и выборка. Выборочный метод опирается на два важных раздела математической статистики - теорию выбора из конечной совокупности и теорию выбора из бесконечной совокупности. Основное отличие выборочный метод для конечной и бесконечной совокупностей заключается в том, что в первом случае выборочный метод применяется, как правило, к объектам неслучайной, детерминированной природы (например, число дефектных изделий в данной партии готовой продукции не является случайной величиной: это число - неизвестная постоянная, которую и надлежит оценить по выборочным данным). Во втором случае выборочный метод обычно применяется для изучения свойств случайных объектов (например, для исследования свойств непрерывно распределённых случайных ошибок измерений, каждое из которых теоретически может быть истолковано как реализация одного из бесконечного множества возможных результатов). . Ген совокупность – совокупность явлений, из которых производится выборка. Та часть объектов, которая отобрана для непосредственного изучения из ген совокупности, называется выборкой. Преимущества выборочного метода: экономит затраты ресурсов, явл-ся единств возможным в случае бесконечной ген сов-ти, дает возм-ть проведения углубленного ися при тез же затратах, позволяется снизить ошибки регистрации.
33. Гистограмма и полигон. Полигон служит дл изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты. (Xi, ni) Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон распределения.
34. Характеристики вариационного ряда. 1. Среднее вариационное (х = Σхi/n) 2. Мат ожидание – чаще всего встречается. 3. Медиана – варианта, которая делит расшифрованный ряд (упорядоченный по возрастанию) на две равные части по числу вариант)
35. Статистические гипотезы. Метода мат статистики позволяют проверить предположения о з-не распределения некоторой случайной величины, о знач-х параметров распределений. Эти задачи мат статистика решает не прямым расчетом, а в виде выдвижения гипотез, тк исходные данные для статистич расчетов являются случ величинами и полученные р-ты расчетов – случ-е величины. Стат гипотеза – любое предположение в виде неизвестного закона распределения или о параметрах известных распределений. Задача проверки стат гипотезы заключается в том, стобы проверить согласуются ли выборочные данные выдвинутой гипотезе.
