Функція двох змінних. Поняття про логічний базис.
До таких функцій належать функції І, АБО, НЕ, І – НЕ, АБО – НЕ , виключне АБО. Кожна з цих функцій може бути відтворена, реалізована конкретним електронним пристроєм.
Кожна функція може бути представлена відповідним електричним пристроєм що їх моделює.
Функціонально повним логічним базисом називається набір логічних операцій, за допомогою яких можна представити будь-яку нулеву функцію. Функціонально повними є базиси (І, АБО,НІ). Логічний базис називається мінімальним, якщо видалення хоча б однієї з вхідних функцій перетворюється в набір функціонально неповний.
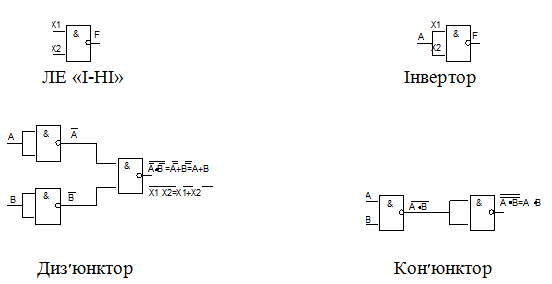
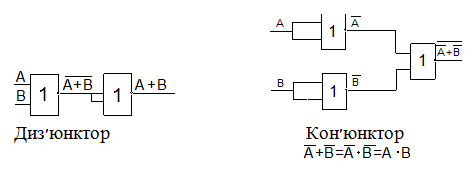
Реалізація логічних функцій в базисі (І-НІ) Реалізація логічних функцій в базисі АБО-НІ
Днф та дднф (кнф та дкнф). Представлення функцій в дднф та дкнф.
Одну
і ту ж булеву функцію можна представити
різними формами. Форми, які представляються
сумою елементарних добутків, – це
диз’юнктивні нормальні форми (ДНФ).
Елементарними називаються такі добутки,
в яких співмножниками є окремі змінні
або їх заперечення
, ..., а ДНФ буде складатись із суми цих
елементарних добутків
.
Очевидно, що одну і ту ж функцію можна представити множиною різних ДНФ. Але є такі ДНФ, в яких функцію можна записати єдиним способом. Такі форми називаються досконалими диз’юнктивними нормальними формами (ДДНФ) – це сума елементарних добутків, в яких кожна змінна трапляється один раз або із запереченням, або без нього.
-
це ДНФ.
Для
перетворення цієї функції в ДДНФ треба
кожен елементарний добуток доповнити
тією змінною, якої бракує, але так, щоб
тотожність не порушувалась. Так, перший
добуток до множимо на
, а другий на
(правило виключення третього). Отримаємо
ДДНФ.
Тут в кожному добутку кожна змінна трапляється тільки один раз.
Ця функція перетворюється в логічну одиницю при трьох різних комбінаціях значень вхідних змінних:
х1 = 1; х2 = 0; х3 = 1 – перша комбінація,
х1 = 0; х2 = 0; х3 = 1 – друга комбінація,
х1 = 1; х2 = 0; х3 = 0 – третя комбінація.
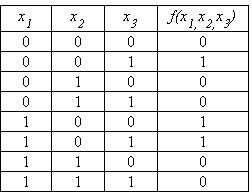Таблиця
істинності для цих змінних (табл.2.3) має
три рядки, в яких функція дорівнює 1.
Тобто, таблиця істинності функції має
стільки рядків, де функція дорівнює 1,
скільки елементарних добутків має її
ДДНФ.
Маючи
таблицю істинності значень функції,
запишемо ДДНФ функції за таким правилом:
для всіх комбінацій вхідних змінних,
для яких функція дорівнює одиниці,
записати добутки, інвертуючи всі змінні,
які в цій комбінації мають нульове
значення, а всі елементарні добутки
з’єднати знаком логічного додавання.
Застосуємо три елементарні добутки:
Якщо їх з’єднати знаком логічного
додавання, то отримаємо ДДНФ.
Логічні
функції які містять тільки кон’юнкцію
окремих членів, кожен з яких є функцією
що містить тільки диз’юнкцію та інверсії
називається - Кон'юнкти́вна
норма́льна фо́рма (КНФ).
Формула називається досконалою кон’юнктивною нормальною (ДКНФ), якщо вона є кон’юнкцією різних повних елементарних диз’юнкцій від висловлювальних змінних. ДКНФ має такі властивості:
у ній немає двох однакових множників;
жодний множник не містить двох однакових доданків;
жодний множник не містить деяку змінну разом з її запереченням;
кожен множник містить як доданок xi або`xi для будь-якого i.