19. Покрытие n-мерного бинарного векторного пространства, Многомерный гиперкуб.

n-мерное векторное пространство:Bⁿ, гдеВ = {0, 1}.

|Bⁿ| = 2ⁿ

Разбиение бинарного векторного пространства:

Возьмём некоторую функцию алгебры логики f: Bⁿ  B.

Множество истинности этой функции: x_lT[f()_n = 1]

Множество ложности: x_lF[f()_n = 0]

Множество, на котором функция не определена: N.

Все эти множества не пересекаются, причём Bⁿ = T  F  N– разбиение, однако…

Покрытие:

Здесь надо говорить про покрытие множества истинности функции (которое, ясен пень, входит в бинарное векторное пространство) множествами истинности импликант этой функции.

Многомерный гиперкуб– это графическое представление всей вышесказанной ботвы.

Этот вопрос наверно можно рассказывать с рисунками и на примере чего-нить.

20. Приведенная система простых ипликант и конъюнктивная форма импликантной матрицы.

Система простых импликант некоторой булевской функции, не содержащая избыточных простых импликант, называется приведенной системой простых импликант.

Избыточная простая импликанта– та, мн-во истинности которой покрывается другими ипликантами.

Для построения приведённой системы простых импликант используют импликантную матрицу. В ней количество столбцов – |T_f| – мощность множества истинности исходной функции; количество строк – мощность системы простых импликант.

Элемент матрицы a_ij = 1, еслиi-ая простая импликанта покрываетj-ую конституэнту единицы, иначеa_ij = 0.

Конъюнктивная форма импликантной матрицыстроится в виде конъюнкции по столбцам дизъюнкций ненулевых элементов каждого столбца. Затем конъюнктивная форма преобразуется в дизъюнктивную (дизъюнкция конъюнкций), в которой каждой конъюнкции соответствует неизбыточная система простых импликант.

21. Теоремы Квайна и Мак-Класски и минимизация булевских функций на n-мерных гиперкубах – доказательство.

Что такое ваще склеивание (т.н. правила склейки):

Теорема Квайна:Для того чтобы 2 конституэнты единицы склеивались необходимо и достаточно, чтобы:

1) | index (x_l ) - index (x_p )|=1

2) _lp = 2^k , kZ⁺

3) | x_l | > | x_p |  index (x_l ) > index (x_p )

Примерное док-во теоремы Квайна:

1. Возьмём 2 склеивающиеся конституэнты единицы. Представим их как кортежи единичек и ноликов. У них все разряды кроме одного одинаковые. Сложим их по модулю 2 (эта операция эквивалентна операции взятия разности их модулей). Получаем что их сумма по модулю (она же разность модулей) 2 равна целой степени двойки: x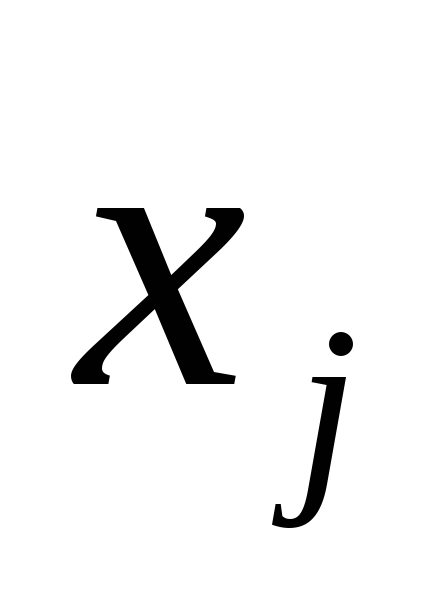₁… …x_n x₁… …x_n = 0 …0 1 0 … 0 = 2 ^j-1. Т.о. доказали теорему в одну сторону.

2. В обратную сторону – х.з., как. =( Но в общем-то аналогично. ;)

Теорема Мак-Класски:

Необходимыми и достаточными условиями склеивания импликант произвольного уровня являются:

1) Равенство последовательностей разностей

2) Возможность склеивания младших конституэнт единицы в склеиваемых импликантах.

Ооооочень примерное док-во теоремы Мак-Класски:

Импликанта – «сборище» конституэнт.

Равенство последовательностей разностей нужно для того, чтоб соответствующие элементы гиперкуба «не пересекались».

Короче, это *дец. Эту теорему, если, не дай Бог она попадётся, лучше «показывать» на примере.