23. Система переходов Келлера: определение, способы задания. Представление асинхронных процессов.

Система переходов Келлера – это двойка <S, F>, где S – нек. конечное мн-во символов, которые будем называть состояниями, а F – бинарное отношение на этом множестве.

Любой кортеж на доменом S будет называться процессом, если отношение порядка в этом кортеже будет согласовано с б.о. непосредственного следования F данной системы переходов.

Т.е. представление пр-ссов в этой метамодели – кортежи состояний (вроде как…).

Граф:

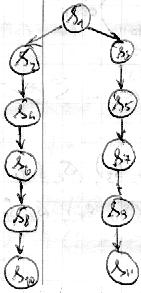
24. Отношение непосредственного следования на множестве состояний системы переходов.

F– бинарное отношение непосредственного следования (частный случай порядка)

– бинарное отношение достижимости (транз. замыканиеF)

Свойства б.о. F:

1) Антирефлексивность (если на графе есть петли, то иррефлексивность)

2) Антисимметричность

3) [Транзитивность] (которой может и не быть)

25. Свойства потокового отношения (отношения непосредственного следования). Замыкание отношения непосредственного следования. Свойство сходимости системы.

Свойства бинарного отношения следования:

1. Антирефлексивность (если на графе появляются петли, то иррефлексивность).

2. Антисимметричность

3. [Транзитивность] – т.е. может быть или не быть

Транзитивное замыкание: .

Транзитивное замыкание является бинарным отношением достижимости.

Помеченная система переходов Келлера: четвёрка объектов < S, F, A, λ >, где S = {s₁, ..., s_n}; F S × S; A = {α, β, γ, ...}; λ: F → A – функция пометки рёбер (не явл. взаимнооднозн. соответствием, но явл. функцией; разные ребра могут иметь одну метку).

(si sj)  F si F sj

si →^α sj или si (α) sj

Порождающая система всегда одна, а помеченных систем – сколько угодно.

Сходимость

Теорема Рассела-Черча: Если метамодель обладает свойством сходимости, то такая система порождает процессы, приводящие к одному результату.

Эта теорема объясняет, зачем вообще нужно это свойство сходимости: процессы, порождаемые системой, обладающей этим св-вом, приводят к 1-му результату.

Теорема (Келлер): Если асинхронные процессы, порождаемые некоторой метамоделью, обладают локальными свойствами детерминированности, коммутативности и устойчивости, то такая метамодель обладает свойством сходимости.

1. Св-во лок. детерминированности: s_i, s_j, s_k  S σ  A [ s_i (σ) s_j & s_i (σ) s_k → s_j = s_k ]

т.к. σ  A, то это локальное свойство. s_i (σ) s_j можно записать s_i → ^σ s_j

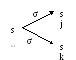
2. Св-во лок. коммутативности: s_i, s_j, s_k  S σ, π  A [ s_i (σ π) s_j  F⁺ & s_i (π σ) s_k  F⁺ → s_j = s_k ]

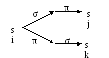
3. Св-во устойчивости: s_i, s_j, s_k  S σ, π  A s_m  S [ s_i (σ) s_j  F & s_i (π) s_k  F → s_i (π σ) s_m  F⁺ ]

Считается, что у s_i потенциально разрешены два действия: π и σ. Мы рассматриваем вариант, когда выполняется π. Выполнение одного из разрешенных действий не снимает разрешение с остальных действий.

Теорема (сходимости Келлера):

Система переходов <S,F> некоторой помеченной системы <S,F,A,D> является сходящейся т. и т.т., к. помеченная система переходов обладает свойствами локальной детерминированности, локальной коммутативности и устойчивости.