
- •Интегральные характеристики индивидуального объема жидкости
- •Полная производная по времени от интегральной характеристики индивидуального объема
- •Контрольная поверхность
- •4.2. Закон сохранения массы
- •4.3. Закон изменения количества движения
- •4.4. Закон о изменения кинетической энергии
- •Расходомер Вентури
- •Уравнение Бернулли для линии тока идеальной несжимаемой жидкости
- •Трубка Пито-Прандтля
- •4.5. Закон изменения полной энергии
- •Распределение температуры в трубопроводе. Формула в.Г.Шухова.
- •4.6. Закон изменения момента количества движения
- •Уравнение л.Эйлера для насоса
- •5. Уравнения гидромеханики в дифференциальной форме
- •5.1. Интегральная теорема Гаусса-Остроградского
- •5.2. Дифференциальное уравнение неразрывности
- •5.3. Дифференциальные уравнения движения сплошной среды
- •5.4. Течение идеальной жидкости. Уравнения Эйлера
- •5.5. Течение вязкой ньютоновской жидкости. Уравнения Навье-Стокса
- •6. Размерность величин и подобие явлений
- •6.1. Размерные и безразмерные величины
- •Первичные (основные) и вторичные (производные) единицы измерения
- •6.2. Формула размерности.
- •Доказательство формулы размерности
- •6.3. Основной вопрос теории размерности
- •6.4. Размерно-зависимые и размерно-независимые величины
- •6.5. Доказательство основной теоремы теории размерности ( теорема Букингема)
- •6.6. Пример: движение вязкой жидкости в цилиндрических трубах
- •6.7. Подобие и моделирование физических явлений
- •Критерии подобия и техника моделирования
4.5. Закон изменения полной энергии
Теорема живых сил, речь о которой шла в предыдущем параграфе, представляет собой закон изменения кинетической энергии системы материальных точек, являющийся следствием законов механики. Однако существует другой, более фундаментальный закон физики – закон об изменении полной энергии тела, составляющий так называемое первое начало термодинамики. Этот закон гласит: изменение полной энергии любого тела (твердого, жидкого, газообразного и т.д.) равно сумме работы внешних сил и внешнему притоку тепла. Иными словами, закон об изменении полной энергии тела утверждает, что изменить эту энергию можно только за счет притока (или оттока) энергии извне - либо в виде работы внешних сил, либо в виде внешнего тепла, либо того и другого вместе взятых. В случае если работа внешних сил и приток внешнего тепла отсутствуют, полная энергия тела не изменяется. Последнее утверждение известно как закон сохранения полной энергии тела.
Относя
притоки энергии к единице времени, можно
говорить об интенсивности
![]() притока внешнего тепла и о мощности
притока внешнего тепла и о мощности
![]() внешних сил:
внешних сил:
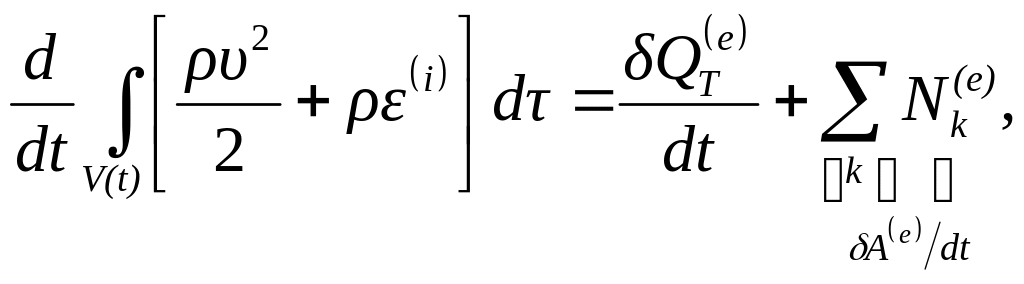 (4.53)
(4.53)
где
![]() плотность
внутренней энергии
- внутренняя энергия единицы массы
среды,
плотность
внутренней энергии
- внутренняя энергия единицы массы
среды,
![]() ;
;
![]() интенсивность притока внешнего тепла
(Вт).
Символ
интенсивность притока внешнего тепла
(Вт).
Символ
![]() используется здесь, чтобы подчеркнуть,
что в общем случае величины
используется здесь, чтобы подчеркнуть,
что в общем случае величины
![]() и
и
![]() не являются
полными дифференциалами каких-либо
функций; функций состояния
не являются
полными дифференциалами каких-либо
функций; функций состояния
![]() и
и
![]() не существует.
не существует.
Уравнение (4.53), представляющее выражение 1-го начала термодинамики, читается так: скорость изменения полной энергии системы материальных частиц, составляющих подвижный объем , равна интенсивности притока внешнего тепла, сложенной с суммарной мощностью всех внешних сил. Важно подчеркнуть, что в этот закон входят только внешние притоки энергии.
Если из уравнения (4.53) исключить изменение кинетической энергии с помощью уравнения (4.3), то получится уравнение, называемое уравнением притока тепла:
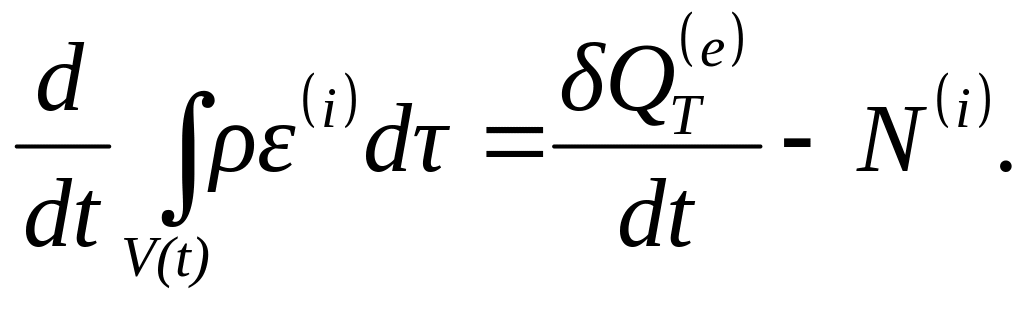 (4.54)
(4.54)
В это уравнение, определяющее скорость изменения внутренней энергии объема жидкости V(t), входят интенсивность внешнего притока тепла и мощность внутренних сил.
Преобразуя левую часть уравнения (4.54) с помощью основной формулы (4.10), получаем:
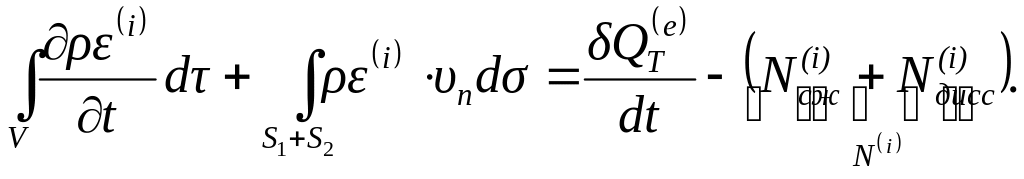 .
(4.55)
.
(4.55)
Для несжимаемой жидкости , поэтому уравнение (4.55) имеет вид:
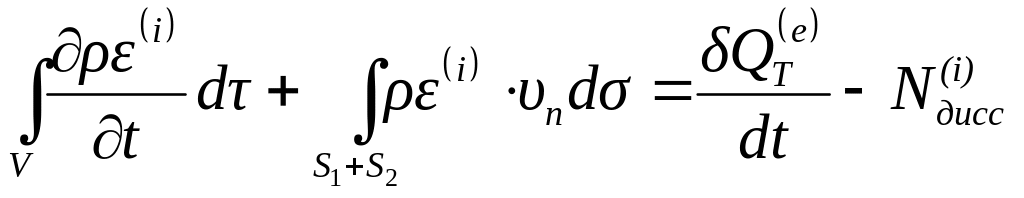 .
(4.56)
.
(4.56)
Если
рассматривать к тому же установившееся
течение жидкости, для которого
![]() ,
то уравнение упрощается еще больше:
,
то уравнение упрощается еще больше:
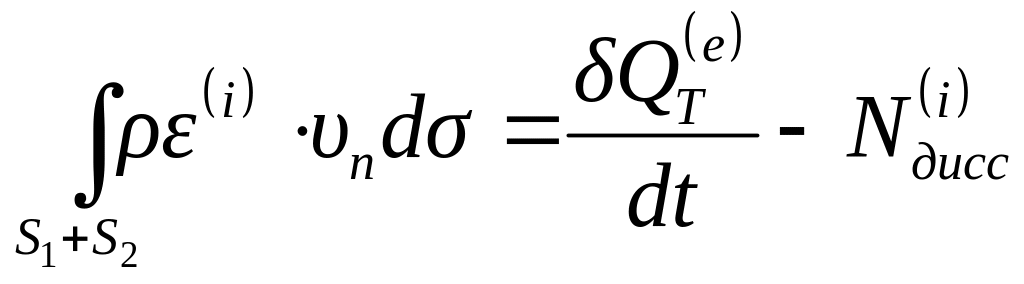 .
(4.57)
.
(4.57)
Распределение температуры в трубопроводе. Формула в.Г.Шухова.
Применим
полученное уравнение (4.57) для расчета
распределение температуры
![]() по длине участка трубопровода с постоянным
диаметром
по длине участка трубопровода с постоянным
диаметром
![]() при установившемся неизотермическом
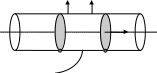
течении несжимаемой жидкости. Выберем
контрольную поверхность
,
состоящую из трех частей:
при установившемся неизотермическом
течении несжимаемой жидкости. Выберем
контрольную поверхность
,
состоящую из трех частей:
![]() поперечное сечение трубы
поперечное сечение трубы
![]() ;
;
![]() поперечное сечение трубы
поперечное сечение трубы
![]() ;
;
![]() внутренняя поверхность трубы на участке
внутренняя поверхность трубы на участке
![]() ,
причем
,
причем
![]() (рис. 4.14).
(рис. 4.14).
![]()
![]()
![]()
![]()
![]()
Рис. 4.14. Неизотермическое установившееся течение
жидкости в трубопроводе
Поскольку
на
:
![]() ,
на
:
,
на
:
![]() и на
:
и на
:
![]() ,
то из (4.54) получаем:
,
то из (4.54) получаем:
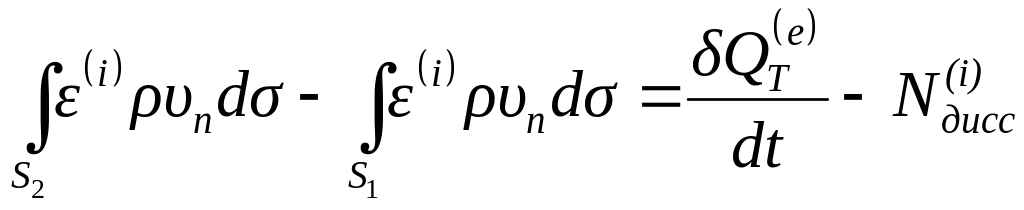 .
.
Далее имеем:
![]()
![]() .
(4.58)
.
(4.58)
Примем следующие допущения:
а) Внутренняя энергия жидкости с точностью до постоянной величины определяется равенством
![]() ,
,
где
![]() — теплоемкость жидкости при постоянном
объеме (
— теплоемкость жидкости при постоянном
объеме (![]() );
);
![]() — абсолютная температура;
— абсолютная температура;
б)
Приток внешнего тепла происходит только
через поверхность трубы
![]() и определяется интегралом
и определяется интегралом
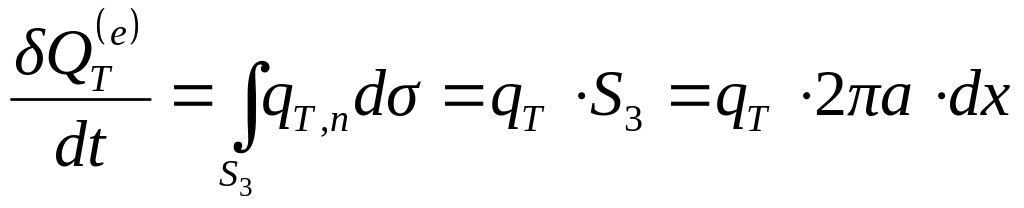 ,
,
где
![]() секундный поток тепла через единицу
поверхности трубы, (
секундный поток тепла через единицу
поверхности трубы, (![]() ).
).
в)
Секундный поток тепла
![]() пропорционален разности температур
пропорционален разности температур
![]() жидкости в трубе и окружающей среды
жидкости в трубе и окружающей среды
![]() (формула Ньютона), так что
(формула Ньютона), так что
![]() .
(4.59)
.
(4.59)
Коэффициент
![]() ,
входящий в формулу (4.59), называется
коэффициентом
теплопередачи.
Знак минус показывает, что тепло
передаются в направлении от большей
температуры к меньшей:
,
входящий в формулу (4.59), называется
коэффициентом
теплопередачи.
Знак минус показывает, что тепло
передаются в направлении от большей
температуры к меньшей:
![]() ,
если
,
если
![]() (отбор тепла от жидкости в трубе);
(отбор тепла от жидкости в трубе);
![]() ,
если
,
если
![]() (приток тепла к жидкости в трубе);
(приток тепла к жидкости в трубе);
г)
Суммарная мощность
![]() диссипативных сил вязкого внутреннего
трения между сечениями
диссипативных сил вязкого внутреннего
трения между сечениями
![]() и
и
![]() можно представить как произведение
можно представить как произведение
![]() мощности этих сил в единице массы
жидкости (удельной мощности) и массы
жидкости
мощности этих сил в единице массы
жидкости (удельной мощности) и массы
жидкости
![]() :
:
![]() .
.
Используя принятые допущения, получаем из уравнения (4.58) уравнение
![]() ,
,
которое
после деления на
![]() дает дифференциальное уравнение для
температуры
:
дает дифференциальное уравнение для
температуры
:
![]() .
(4.60)
.
(4.60)
Уравнение
(4.60) может быть проинтегрировано в
случае, если принять, что
![]() ,
,![]() и
есть постоянные величины. Кроме того,
и
есть постоянные величины. Кроме того,
![]()
Если
в начальном сечении трубопровода
![]() температура жидкости равна
температура жидкости равна
![]() ,
то решение этого уравнения имеет вид:
,
то решение этого уравнения имеет вид:
 ,
(4.61)
,
(4.61)
где
![]() внутренний диаметр трубопровода.
внутренний диаметр трубопровода.
Формула (4.61) носит название формула В. Г. Шухова. (В.Г.Шухов - выдающийся русский инженер, архитектор, изобретатель и ученый, 1853-1939). Первое слагаемое в правой части этой формулы определяет изменение температуры жидкости за счет теплообмена с окружающей средой, второе слагаемое связано с нагреванием жидкости за счет диссипации механической энергии.
Вводя
параметр
![]() :
:
![]() ,
,
имеющий размерность температуры и отражающий переход механической энергии в тепло, формулу В.Г.Шухова можно записать проще:
![]() .
(4.62)
.
(4.62)
Эта формула показывает, что выделение тепла при трении слоев жидкости друг относительно друга эквивалентно увеличению наружной температуры на величину .
Распределение
температуры
по длине участка трубопровода показано
на рис. 4.16 [ ]. Из графиков на этом рисунке
видно, что в случае
![]() жидкость, текущая в трубопроводе,
охлаждается, наоборот, в случае, когда
жидкость, текущая в трубопроводе,
охлаждается, наоборот, в случае, когда
![]() ,
жидкость нагревается. В обоих случаях
,
жидкость нагревается. В обоих случаях
![]() .
.
Т
![]()


![]()
![]()

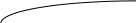


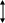
T
0
![]()
![]()

Рис.4.16. Распределение температуры
по длине участка трубопровода
Температуру
![]() жидкости в конце участка трубопровода
можно вычислить с помощью решения
(4.62), положив в нем
жидкости в конце участка трубопровода
можно вычислить с помощью решения
(4.62), положив в нем
![]() .
Имеем:
.
Имеем:
![]() ,
(4.63)
,
(4.63)
где
![]() длина участка.
длина участка.
