3.2 Классификация игр

Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д.

В зависимости от количества игроков различают игры двух и n игроков. Первые из них наиболее изучены. Игры трёх и более игроков менее исследованы из-за

возникающих принципиальных трудностей и технических возможностей получения решения. Чем больше игроков - тем больше проблем.

По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий игра называется бесконечной.

По характеру взаимодействия игры делятся на:

бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции;

коалиционные (кооперативные) – могут вступать в коалиции.

В кооперативных играх коалиции наперёд определены.

По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.

По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др.

Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 2, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).

Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путём сведения игры к задаче линейного программирования.

Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)

Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные.

Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения.

Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определённого числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.

3.3 Математическая формализация игровых задач

Критерий Сэвиджа — один из критериев принятия решений в условиях неопределённости. Условиями неопределённости считается ситуация, когда последствия принимаемых решений неизвестны, и можно лишь приблизительно их оценить. Для принятия решения используются различные критерии, задача которых — найти наилучшее решение максимизирующее возможную прибыль и минимизирующее возможный убыток.

Критерий заключается в следующем:

1. Строится матрица стратегий. Столбцы соответствуют возможным исходам. Строки соответствуют выбираемым стратегиям. В ячейки записывается ожидаемый результат при данном исходе и при данной выбранной стратегии.

2. Строится матрица сожаления. В ячейках матрицы величина сожаления — разница между максимальным результатом при данном исходе (максимальном числе в данном столбце) и результатом при выбранной стратегии. Сожаление показывает величину, теряемую при принятии неверного решения.

3. Минимаксное решение соответствует стратегии, при которой максимальное сожаление минимально. Для этого для каждой стратегии (в каждой строке) ищут максимальную величину сожаления. И выбирают то решение (строку), максимальное сожаление которого минимально.

Критерий Сэвиджа стремится смягчить консерватизм минимаксного (максиминного) критерия путем замены матрицы платежей (выигрышей или проигрышей) v(аi, sj) матрицей потерь r(аi, sj), которая определяется следующим образом.

Он основан на принципе минимизации потерь, связанных с тем, что игрок А принял не оптимальное решение. Для решения задачи составляется матрица потерь, которая называется матрицей рисков , которая получается из матрицы выигрышей путем вычитания из максимального элемента каждого столбца всех остальных элементов.

Критерий Гурвица – это взвешенная позиция “пессимизма-оптимизма”.

Этот критерий охватывает ряд различных подходов к принятию решений — от наиболее оптимистичного до наиболее пессимистичного (консервативного). Пусть 0 <= а <= 1 и величины v(аi, sj) представляют доходы. Тогда решению, выбранному по критерию Гурвица, соответствует

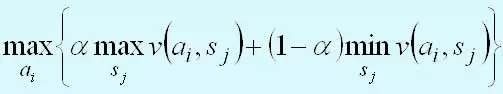
Параметр а - показатель оптимизма.

Если a = 0, критерий Гурвица становится консервативным, так как его применение эквивалентно применению обычного минимаксного критерия.

Если а = 1, критерий Гурвица становится слишком оптимистичным, ибо рассчитывает на наилучшие из наилучших условий.

Можно конкретизировать степень оптимизма (или пессимизма) надлежащим выбором величины a интервала [0,1]. При отсутствии ярко выраженной склонности к оптимизму или пессимизму выбор а = 0,5 представляется наиболее разумным.

Если величины v(аi, sj) представляют потери, то критерий принимает следующий вид:

Это самый универсальный критерий, который позволяет управлять степенью «оптимизма - пессимизма» игрока А. Введем некоторый коэффициент a, который назовем коэффициентом доверия или коэффициентом оптимизма. Этот коэффициент можно интерпретировать как вероятность, с которой произойдет наилучший для А исход. Исходя из этого, наихудший вариант можно ожидать с вероятностью (1-α). Коэффициент доверия a показывает, насколько игрок А может управлять ситуацией и в той или иной степени рассчитывает на благоприятный для него исход. Если вероятности благоприятной и неблагоприятной ситуации для А равны, то следует принять α=0,5.

Для реализации критерия Гурвица вычисляются максимальные и минимальные показатели для каждой альтернативы , и функции полезности.

Критерий Лапласа опирается на принцип недостаточного основания, который гласит, что, поскольку распределение вероятностей состояний P(si) неизвестно, нет причин считать их различными. Следовательно, используется оптимистическое предположение, что вероятности всех состояний природы равны между собой, т.е. P{s1} = P{s2} = ... = P{sn} = 1/n. Если при этом v(аi, sj) представляет получаемую прибыль, то наилучшим решением является то, которое обеспечивает

Если величина v(аi, sj) представляет расходы лица, принимающего решение, то оператор "max" заменяется на "min".

Он основан на предположении, что каждый вариант развития ситуации (состояния «природы») равновероятен. Поэтому, для принятия решения, необходимо рассчитать функцию полезности для каждой альтернативы, равную среднеарифметическому показателей привлекательности по каждому «состоянию природы»:

Критерий Лапласа определяет оптимальное решение по минимальной функции полезности.

В основе этого критерия лежит "принцип недостаточного основания": если нет достаточных оснований считать, что вероятности того или иного спроса имеют неравномерное распределение, то они принимаются одинаковыми и задача сводится к поиску варианта, дающего

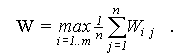
3.4 Решение игры с помощью критерия Гурвица,Севиджа,Лапласса

Решение задачи с помощью критерия Гурвица

	В1	В2	В3	В4
А1	8	3	9	12
А2	7	6	8	14
А3	9	2	5	1

Max{min α+(1- α)max

При α=0,2

0,2*3+(1-0,2)*12=10,2

0,2*6+(1-0,2)*14=12,4

0,2*1+(1-0,2)*19=7,4

max=12,4.По критерию Гурвица оптимальной стратегией является A₂ .

При α=1,2

1,2*3+(1-1,2)*12=1,2

1,2*6+(1-1,2)*14=4,4

1,2*1+(1-1,2)*9=-0,6

max=1,2.По критерию Гурвица оптимальной стратегией является A₂ .

Решение задачи с помощью критерия Севиджа

	В1	В2	В3	В4
А1	8	3	9	12
А2	7	6	8	14
А3	9	2	5	1

Матрица рисков

1	3	0	2	3
2	0	1	0	2
0	4	4	13	13

Min=2. .По критерию Гурвица оптимальной стратегией является 2

Решение задачи с помощью критерия Лапласса

	В1	В2	В3	В4
А1	8	3	9	12
А2	7	6	8	14
А3	9	2	5	1

P₁=P₂=P₃=P₄=0,25

0,25*(8+3+9+12)=8

0,25*(7+6+8+14)=8,75

0,25*(9+2+5+1)=4,25

max=8,75. По критерию Лапласса оптимальной стратегией является A₂ .