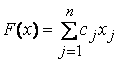1 Линейное программирование

1.1 Постановка задачи

     Линейное программирование — раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.      Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов.      Формы записи задачи линейного программирования:      Общей задачей линейного программирования называют задачу                          (2.1)      при ограничениях                       (2.2)                           (2.3)                            (2.4)                                   (2.5)       - произвольные                   (2.6)      где   - заданные действительные числа; (2.1) – целевая функция; (2.1) – (2.6) –ограничения;   - план задачи.      Пусть ЗЛП представлена в следующей записи:                                                        (2.7)                                         (2.8)                                             (2.9)      Чтобы задача (2.7) – (2.8) имела решение, системе её ограничений (2.8) должна быть совместной. Это возможно, если  r этой системы не больше числа неизвестных n. Случай r>n вообще невозможен. При r=n система имеет единственное решение, которое будет при  оптимальным. В этом случае проблема выбора оптимального решения теряет смысл. Выясним структуру координат угловой точки многогранных решений. Пусть r<n. В этом случае система векторов  содержит базис — максимальную линейно независимую подсистему векторов, через которую любой вектор системы может быть выражен как ее линейная комбинация. Базисов, вообще говоря, может быть несколько, но не более  . Каждый из них состоит точно из r векторов. Переменные ЗЛП, соответствующие r векторам базиса, называют, как известно, базисными и обозначают БП. Остальные n – r переменных будутсвободными, их обозначают СП. Не ограничивая общности, будем считать, что базис составляют первые m векторов  . Этому базису соответствуют базисные переменные  , а свободными будут переменные  .      Если свободные переменные приравнять нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (8) называют опорным решением (планом).      Теорема. Если система векторов   содержит m линейно независимых векторов  , то допустимый план                                         (2. 10)      является крайней точкой многогранника планов.      Теорема. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.

1.2 Формы записи задачи линейного программирования

1. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

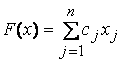(10.10)

при условиях

(10.11)

(10.12)

.                                 (10.13)

Функция  (10.10) называется целевой функцией (или линейной формой) задачи (10.10) – (10.13), а условия (10.11) – (10.13) – ограничениями данной задачи.

2. Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального для «≤» (минимального для «≥») значения функции (10.10) при выполнении условий (10.11) и (10.13), где k = m, s = n.

3. Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (10.10) при выполнении условий (10.12) и (10.13), где k = 0, s = n.

Каноническая (основная) форма	Стандартная (симметричная) форма	Общая форма
1) ограничения
Уравнения .	Неравенства .	Уравнения и неравенств .
2) условия неотрицательности
Все переменные ,	Все переменные ,	Часть переменных ,  ,  .
3) цель задачи
max F(x) или minF(x)	max F(x) [min F(x)]	max F(x) или min F(x)

Замечание.

max F(x) = – min[– F(x)], min F(x) = – max[– F(x)].

Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них может быть преобразована к форме другой. Совокупность чисел  , удовлетворяющих ограничениям (10.11) – (10.13), называется допустимым решением (или планом).

Запишем основную задачу линейного программирования в векторной форме. Найти максимум (минимум) функции

при условиях

,                   (10.14)

где   – скалярное произведение;   и   – m-мерные вектор-столбцы, составленные из коэффициентов при неизвестных и свободных членов системы уравнений задачи.

План Х называется опорным планом основной задачи линейного программирования, если система векторов  , входящих в разложение (10.14) с положительными коэффициентами , линейно независима.

Опорный  план  называется  невырожденным,  если  он  содержит ровно m положительных компонент, в противном случае он является вырожденным.

План  , при котором целевая функция принимает свое максимальное (минимальное) значение, называется оптимальным.

1.3 Модель транспортной задачи

Переменными (неизвестными) транспортной задачи являются x_ij , i=1,2,...,m j=1,2,...,n — объемы перевозок от i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок:

Так как произведение C_ij*X_ij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны:

По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция задачи имеет вид:

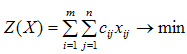
Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью и имеет вид:

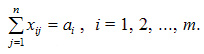
Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид:

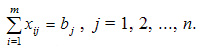
Учитывая условие неотрицательности объемов перевозок математическая модель выглядит следующим образом:

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарынм запросам потребителей, т.е.:

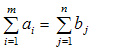
Такая задача называется задачей с правильным балансом, а модель задачи закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а модель задачи — открытой.

1.4 Двойственная задача линейного программирования

Каждой задачи линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой. Дадим определение двойственной задачи по отношению к общей задаче линейного программирования, состоящей в нахождении максимального значения функции

F=c₁x₁+…+c_nx_n (50)

при условиях

a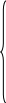 ₁₁x₁+a₁₂x₂₊…+a_1nx_n≤b₁

a₂₁x₁+a₂₂x₂₊…+a_2nx_n≤b₂

_{......................................................}

a_k1x₁+a_k2x₂+…+a_knx_n≤b_k (51)

a_k+11x₁+a_k+12x₂+…+a_k+1nx_n=b_k+1

………………………….

a_m1x₁+a_m2x₂+…+a_mnx_n=b_m

x_i≥0 (i=1,j,j≤n) (52)

Задача, состоящая в нахождении минимального значения функции

F^*=b₁y₁+b₂y₂+..+b_my_m (53)

при условиях

a₁₁y₁+a₂₁y₂₊…+a_m1y_m≥c₁

a₁₂y₁+a₂₂y₂₊…+a_m2y_m≥c₂

_{…………………………………}

a_1iy₁+a_2iy₂₊…+a_miy_i≥c_i (54)

a_1i+1y₁+a_2i+1y₂+..+a_mi+1y_m=c_i+1

a_1ny₁+a_2ny₂+..+a_mny_m=c_m

y_i≥0(i=1,k,k≤m) (55)

называется двойственной по отношению к задаче (50) – (52).

Задачи (50) – (52) и (53) – (55) образуют пару задач, называемую в линейном программировании двойственной парой.

Сравнивая две сформулированные задачи, видим, что двойственная задача по отношению к исходной составляется согласно следующим правилам:

1. Целевая функция исходной задачи (50) – (52) задается на максимум, а целевая функция двойственной (53) – (55) – на минимум.

2. Матрица

a₁₁ a₁₂ … a_1n

A= a₂₁ a₂₂ … a_2n (56)

a_m1 a_m2 … a_mn

составленная из коэффициентов при неизвестных в системе ограничений (51) исходной задачи (50) – (52), и аналогичная матрица

a₁₁ a₁₂ … a_m1

A^’= a₂₁ a₂₂ … a_m2 (57)

a_1n a_2n … a_mn

в двойственной задаче (53) - (55) получаются друг из друга транспонированием (т.е. заменой строк столбцами, а столбцов – строками)

3. Число переменных в двойственной задаче (53) – (55) равно числу соотношений в системе (51) исходной задачи (50) – (52), а число ограничений в системе (54) двойственной задачи – числу переменных в исходной задаче.

4. Коэффициентами при неизвестных в целевой функции (53) двойственной задачи (53) – (55) являются свободные члены в системе (51) исходной задачи (50) – (52), а правыми частями в соотношении системы (54) двойственной задачи – коэффициенты при неизвестных в целевой функции (50) исходной задачи.

1.5 Решение задачи

2 Графы и их применения

2.1 Основные понятия и определения теории графов

Пусть дано множество Х, которое состоит из элементов, называемых точками. Дан закон, позволяющий установить соотношение Т между каждым элементом множества Х и некоторыми из его подмножеств. Обозначим через Тх некое подмножество множества Х, отвечающее элементу х множества Х. Две математические величины – «множество Х» и «соответствие Т» - определяют граф G, обозначаемый как G = (X, T). Элементы множества Х будем изображать точками, и называть вершинами графа. Соотношения Т будем изображать отрезками (иногда ориентированными), соединяющими элемент с элементами подмножества Тх, и называть ребрами или дугами графа. Граф G называется конечным, если число его вершин конечно. На рис.1,а показан граф, определяемый множеством

X = {x0, x1, x2, x3, x4, x5}.

а)

Х₁

Х₃

Х_n

Х₄

Х₂

Х₃

б)

в)

Рис.1. Различные графы: а – граф, определяемый множеством вершин Х = {x0, x1, …, x5}; б – нуль граф; в – граф, определяемый множеством вершин Х = {a, b, c, d}.

Соотношение Т характеризуется следующими равенствами:

Tx0 = {x0, x1, x2, x3, x4, x5}

Tx1 = {x0, x2}

Tx2 = {x0, x1, x3}

Tx3 = {x0, x2, x4}

Tx4 = {x0, x3}

Tx5 = {x0}

Пара вершин xi, xj образует ребро, если, либо точка xi принадлежит подмножеству Txj, либо xj принадлежит подмножеству Txi. Если всякая пара этих точек упорядочена, то такая пара определяет дугу графа и граф называется ориентированным (рис1.в). Две точки xi, xj называются смежными, если они определяют ребро или дугу графа. Две различные дуги являются смежными, если они имеют общую вершину. Последовательность дуг, при которой конец одной дуги является началом другой, называется путем. Путь, в котором никакая вершина не встречается дважды, называется элементарным. Если начальная и конечная точки пути совпадают, образуется контур. Длинна пути (контура) – это число дуг, которые его образуют. Петлей называется контур единичной длинны; петля связывает точку саму с собой. Граф называется связным, если для каждой пары вершин существует соединяющая их цепь (рис.1, в).

Граф называется полным, если любая пара его вершин соединена ребром.

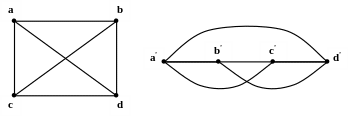
а) б)

Рис.2. Пример полного графа (а) и изоморфный ему граф (б)

Граф является не геометрической, а топологической фигурой. Последней называют такую фигуру, определенные свойства которой инвариантны при взаимнонепрерывном и взаимнооднозначном пространственном преобразовании. Существенные инвариантные свойства графа отражают только число вершин, число дуг (ребер) и характер связей между вершинами. Так как граф является топологической фигурой, то один и тот же граф может быть изображен разными способами (рис.2). Независимо от способа изображения, информация, содержащаяся в графе, остается одной и той же. Два графа будем называть изоморфными, если они имеют одинаковое число вершин, если каждой паре вершин, соединенных ребром в одном графе, соответствует такая же пара вершин, соединенных ребром в другом графе. Обязательным условием изоморфности ориентированных графов является одинаковая ориентация всех дуг.

Представление графов с помощью матриц

Информация, содержащаяся в некотором графе, может быть представлена в алгебраическом виде посредством матриц. Матрицей смежности, соответствующей некоторому графу G = (X, Y), который состоит из n вершин Xi (i = 1, 2, …, n), называется матрица [H] порядка (n×n) с элементами

0, если вершина xi не связана дугой с вершиной xj

hij =

1, если вершина xi связана дугой с вершиной xj

Например, матрица [H] некоторого графа (рис.1, в) имеет следующий вид:

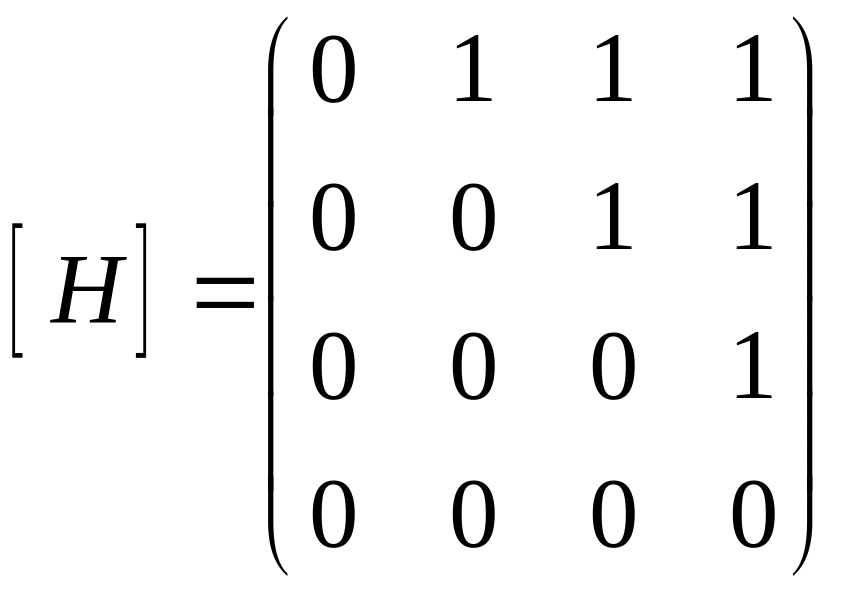
Структурной матрицей, называется матрица, которая соответствует некоторому графу G = (k, q), состоящему из n вершин ki (i = 1, 2, …, n) и из m дуг qj (j = 1, 2, …, m), называется матрица [S] порядка (n×m) с элементами

-1, если дуга qj выходит из вершины ki

s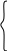 ij = +1, если дуга qj входит из вершины ki

0, если дуга qj не инциндентна вершине ki

В качестве примера составим структурную матрицу для того же графа приведенного на рис.1, в.

j 1 2 3 4 5 6

b

c

d

[S] =

a

Потоковые графы

Каждой ХТС можно поставить в соответствие потоковый граф, гомоморфный рассматриваемой системе и являющийся некоторой топологической моделью одного типа обобщенных или физических потоков данной системы (рис.3). Потоковые графы строят для установившихся технологических режимов.

Рис.3. Потоковый граф ХТС.

Потоковый граф G = G (A) = (A, T) состоит из множеством вершин А, и образован совокупностью элементов, источников и стоков ХТС, и множеством дуг Т. Его элементы соответствуют одного типа обобщенным или физическим потокам системы. Потоковый граф представляет собой некоторое семейство сочетаний или пар вида Т = (а, b), где a Є A, b Є A, указывающее, какие вершины графа являются смежными. Можно выделить три типа потоковых графов ХТС: материальные, тепловые (энергетические), параметрические.

Вершины материального потокового графа по массовому расходу физических потоков (некоторого химического компонента) соответствуют элементам ХТС, которые трансформируют общие массовые расходы физических потоков (химического компонента), источникам и стокам веществ (компонента). Дуги данного графа отвечают обобщенным материальным потокам.

Вершины теплового потокового графа соответствуют элементам системы, которые изменяют расходы тепла физических потоков, внешним и внутренним источникам и стокам тепла ХТС.

Основные особенности материальных потоковых графов и тепловых потоковых графов. 1) ориентированность; 2) ассиметричность, т.к. не все соседние элементы системы связаны между собой обратными технологическими потоками; 3) связность, т.к. все элементы в системе взаимосвязаны единой цепью потоков веществ и энергии.

Параметрические потоковые графы являются топологической моделью, отображающей преобразование элементами системы параметров физических потоков ХТС. Вершины таких графов отвечают элементам, представляющим собой технологические операторы, которые качественно и (или) количественно преобразуют параметры физических потоков, а также источникам и стокам физических потоков ХТС. Дуги графа соответствуют физическим потокам системы. Такие графы являются конечными, ориентированными, ассиметричными, связными.
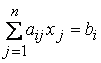
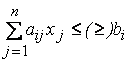
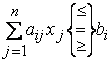