Приложение е математический аппарат электродинамики
В настоящем приложении приводятся основные понятия и формулы, касающиеся комплексных чисел, векторной алгебры и векторного анализа.
Е.1. Комплексные числа
Рассмотрим
комплексную плоскость (рис. Е.1). Каждой
точке комплексной плоскости соответствует
комплексное число
,
которое можно представить в алгебраической
либо показательной формах:
,
,
где
– действительная часть комплексного
числа;
– мнимая часть комплексного числа;
i
– мнимая единица, определяемая формулами
,
.
Из рис. Е.1 и вышеприведенных формул следуют соотношения:
,
,
,
.
Эти формулы позволяют совершить переход от алгебраической формы записи комплексного числа к показательной форме и, наоборот – от показательной к алгебраической.
Сложение
(вычитание) комплексных чисел
и
производится в соответствии с формулами:
.
Умножение комплексных чисел и производится в соответствии с формулами:
.
Деление комплексных чисел и производится в соответствии с формулами:
.
Е.2. Векторная алгебра
Рассмотрим
вектор
.
Его можно представит в общем (некоординатном)
виде как
,
где
– орт (единичный вектор), показывающий
направление вектора
;
– модуль (длина) вектора
.
Вектор также можно представить в виде суммы трех взаимно перпендикулярных векторов.
В декартовой системе координат (x, y, z) это представление имеет вид
.
В цилиндрической системе координат ( , , ) это представление имеет вид
,
где
– орты цилиндрической системы координат
(см. рис. Е.2);
,
– проекции векторов на соответствующие
направления цилиндрической системы
координат.
В сферической системе координат ( , , ) это представление имеет вид
,
где
– орты сферической системы координат
(см. рис. Е.3);
,
– проекции векторов на соответствующие
направления сферической системы
координат.
Рассмотрим
векторы
и
.
Скалярное и векторное произведение
этих векторов определяются формулами:
,
где
– угол между векторами
.
,
где
– единичный вектор нормали к плоскости,
содержащей векторы
и
,
причём
,
и
взаимно перпендикулярны и образуют
“правую тройку”.
Пусть векторы и , представлены через свои проекции в декартовой системе векторов
,
.
В этом случае скалярное и векторное произведение векторов и , можно найти по формулам:
,
.
А
налогичные
представления имеют место для
цилиндрической, сферической и других
ортогональных систем координат.
Рисунок Е.2 – Цилиндрическая система координат
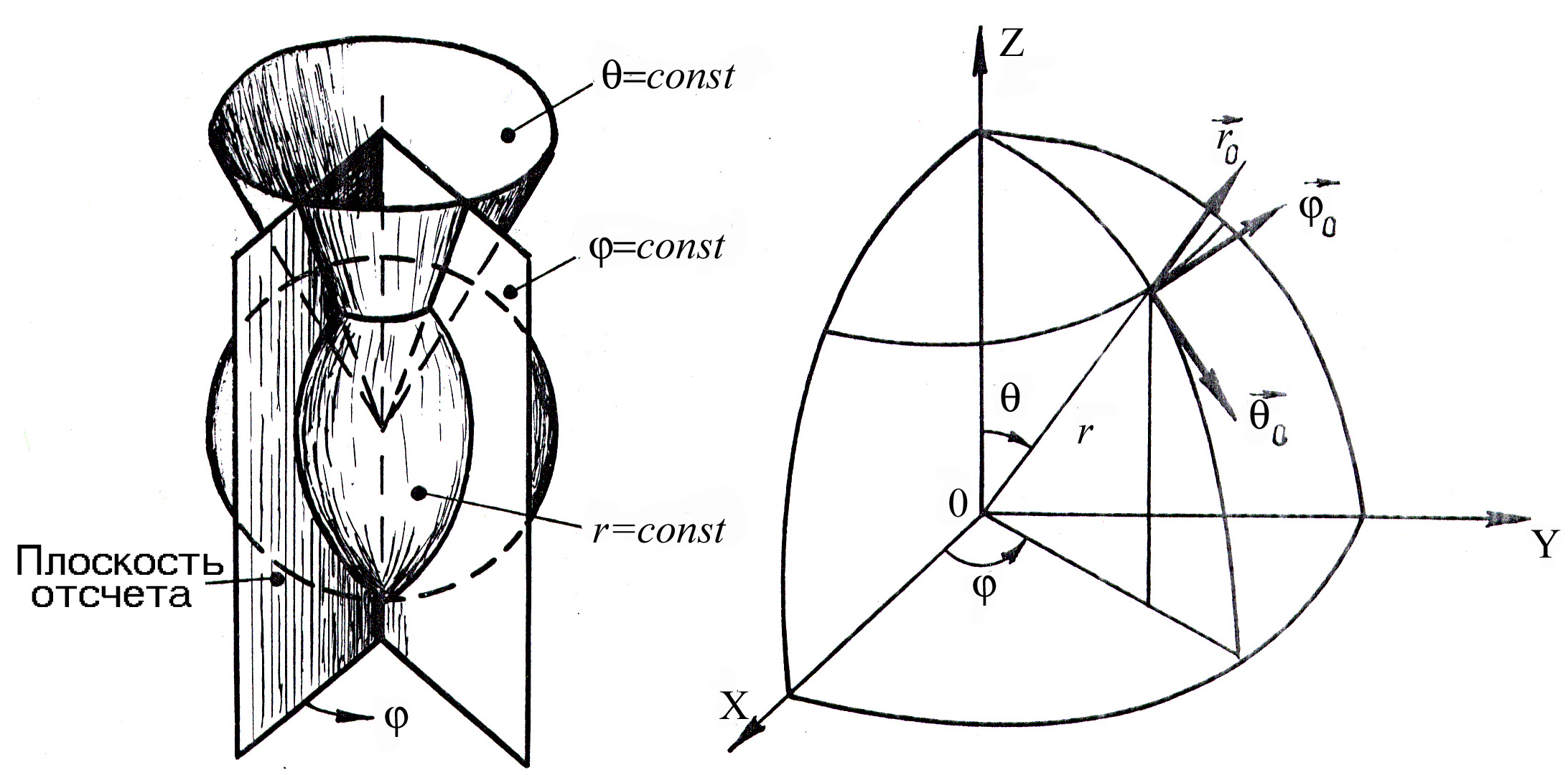
Рисунок Е.3 – Сферическая система координат
Е.3. Векторный анализ
Рассмотрим
операции над скалярной функцией
и векторной функцией
в декартовой, цилиндрической и сферической
системах координат.
Векторный оператор “набла” в декартовой системе координат определяется по формуле:
.
Градиент скалярной функции определяется в соответствующих системах координат по следующим формулам:
,
,
.
Дивергенция (расходимость) векторной функции определяется в соответствующих системах координат по следующим формулам:
,
,
.
Скалярный оператор Лапласа функции определяется в соответствующих системах координат по следующим формулам:
,
,
.
Ротор (вихрь) векторной функции определяется в соответствующих системах координат по следующим формулам:
,
Е.4. Интегральные формулы векторного анализа
Теорема Остроградского-Гаусса
.
Теорема Стокса
.
Теорема Грина
.
В интегральных формулах приняты следующие обозначения:
,
– единичный вектор внешней нормали к
поверхности S,
которая ограничивает объем
;
,
– единичный вектор касательной к контуру
L, на
который опирается поверхность S.
Е.5. Дифференциальные формулы векторного анализа
,
,
,
,
,
,
.
*)
Здесь и далее последняя цифра индекса
при величинах Н или Е равна
числу полуволн стоячей волны,
укладывающихся вдоль оси
резонатора