Приложение в вывод граничных условий для векторов электромагнитного поля

Как отмечалось в подразд. 1.5, уравнения Максвелла в дифферен­циальной форме не пригодны на границе раздела двух сред. Это связано с тем, что при переходе через границу раздела двух сред векторы электромагнитного поля испытывают скачкообразные изменения. Соотношения между векторами в двух очень близких точках, находящихся по обе стороны границы раздела двух сред, называются граничными условиями. Граничные условия являются следствием уравнений Максвелла в интегральной форме и определяются равенствами следующего вида:

, , (В.1)

, , (В.2)

, , (В.3)

, , (В.4)

где – нормаль к границе раздела S, направленная из второй среды в первую, – векторы, лежащие в плоскости Р, которая является касательной к границе раздела. При этом (см. рис. В.1)

Рисунок В.1 – К пояснению граничных условий

Равенства (В.1) и (В.2) определяют граничные условия для касательных составляющих вектора напряженности магнитного и электрического поля, а равенства (В.3) и (В.4) – для нормальных составляющих векторов электрической и магнитной индукции. Первая формула в этих равенствах дает векторную форму граничного условия, а вторая – скалярную форму.

Настоящее приложение посвящено выводу граничных условий.

В.1. Вывод граничных условий для касательных составляющих векторов напряженности магнитного поля

Рассмотрим произвольную точку границы раздела (S) двух изотропных сред. Проведем в этой точке из второй среды в первую единичную нормаль (см. рис. В.2). Рассмотрим плоскость , проходящую через нормаль . На линии пересечения границы раздела и плоскости выделим достаточно малый отрезок так, чтобы выбранная точка находилась внутри этого отрезка. Размеры этого отрезка должны быть такими, чтобы его можно было считать прямолинейным, и чтобы в обеих средах вектор можно было считать постоянным в пределах . В плоскости на отрезке построим прямоугольный контур высоты так, чтобы одна его часть находилась в первой, а вторая – во второй среде. Проведем в выбранной точке орты и . Орт направлен по касательной к отрезку , а орт направлен по нормали к плоскости и так, чтобы выполнялось соотношение

. (В.5)

Р ассмотрим первое уравнение Максвелла в интегральной форме

.

Подставим в это уравнение формулу (1.2) для тока , тогда оно принимает следующий вид:

. (В.6)

Отметим, что в уравнении (В.6) контур является произвольным, а поверхность должна быть такой, чтобы ее края совпадали с контуром . Принято говорить, что поверхность опирается на контур .

Внесем в (В.6) производную по времени под знак интеграла и запишем уравнение (В.6) для контура , тогда получим, что

, (В.7)

где – площадь, охватываемая контуром , а .

Представим левую часть равенства (В.7) в виде суммы четырех интегралов

. (В.8)

Устремим в (В.8) высоту контура к нулю так, чтобы стороны и оставались в разных средах и в пределе совпали с отрезком , тогда второе и четвертое слагаемые в (В.8) стремятся к нулю (к нулю стремятся пределы интегрирования, а подынтегральные функции конечны). В этом случае соотношение (В.8) принимает следующий вид:

, (В.9)

где и – векторы напряженности магнитного поля на отрезке со стороны первой и второй среды.

Учитывая, что , и тот факт, что вектор можно считать постоянным в пределах отрезка , получаем следующее равенство:

. (В.10)

Учтем в последнем равенстве, что , тогда

. (В.11)

Вычислим теперь правую часть соотношения (В.7) при . Очевидно, что при этом . Учтем, что величина является всегда ограниченной величиной. Рассмотрим случай, когда граница раздела не является поверхностью идеального проводника. В этом случае объемная плотность тока проводимости также является ограниченной величиной и

. (В.12)

Подставим равенства (В.11) и (В.12) в соотношение (В.7), тогда получаем, что

.

Учитывая свойство скалярного произведения и тот факт, что , получаем следующее соотношение

. (В.13)

Сравнивая соотношения (В.13) и второе соотношение (В.1), видим, что для рассматриваемого случая, когда объемная плотность тока проводимости ограничена, а значит когда , они совпадают.

Пусть теперь . Это соответствует случаю, когда граница раздела является поверхностью идеального проводника. В этом случае

.

Подставим последнее равенство и равенство (В.11) в соотношение (В.7), тогда получаем, что

. (В.14)

Сократим равенство (В.14) на . Учитывая свойство скалярного произведения и тот факт, что , получаем следующее соотношение

.

Последнее соотношение совпадает со вторым соотношением в формуле (В.1). Отметим, что оно является общим видом граничного условия для касательных составляющих вектора напряженности магнитного поля. В случае, когда , оно совпадает с условием (В.13).

Получим теперь векторную форму граничного условия. Для этого учтем очевидное равенство . Подставляя это равенство в (В.14), получаем, что

.

Учитывая свойства смешанного произведения трех векторов, можно записать, что

.

Поскольку последнее равенство справедливо при любом направлении орта , которое определяется ориентацией контура , то из него следует, что

. (В.15)

Последнее равенство совпадает с первым соотношением формулы (В.1). Это равенство является векторной формой записи граничного условия для касательных составляющих векторов напряженности магнитного поля.

В.2. Вывод граничных условий для касательных составляющих векторов напряженности электрического поля

Рассмотрим второе уравнение Максвелла в интегральной форме

, (В.16)

Из сравнения уравнений (В.6) и (В.16) видно следующее. Если в уравнении (В.6) вектор поменять на вектор , вектор на вектор , а вектор приравнять нулю, то оно переходит в уравнение (В.16). Отсюда следует, что вывод граничных условий для касательных составляющих векторов напряженности электрического поля (формулы (В.2)) проводится по той же методике, что и вывод, проведенный в предыдущем пункте (с учетом указанных изменений).

В.3. Вывод граничных условий для нормальных составляющих векторов электрической индукции

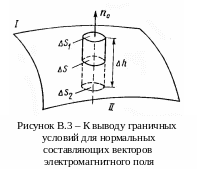
Рассмотрим произвольную точ­ку границы раздела (S) двух изотроп­ных сред. Проведем в этой точке из второй среды в первую единичную нормаль (см. рис. В.3). Выберем в окрестности этой точки достаточно малую поверхность так, чтобы ее можно было считать плоской, и чтобы в обеих средах вектор можно было считать постоянным в пределах . Построим на элементе прямой цилиндр высотой так, чтобы его основания находились в разных средах.

Рассмотрим третье уравнение Максвелла в интегральной форме

. (В.17)

Подставим в это уравнение соотношение (1.1), связывающее заряд и его объемную плотность , тогда

. (В.18)

Отметим, что в уравнении (В.18) замкнутая поверхность , ограничивающая объем , является произвольной.

Запишем уравнение (В.18) для поверхности цилиндра, указанного выше, тогда получим, что

. (В.19)

Представим интеграл в левой части равенства (В.19) в виде суммы интегралов по основаниям цилиндра и его боковой поверхности. Учитывая, что основания цилиндра находятся в разных средах, получаем следующее соотношение:

, (В.20)

где и векторы, направленные вдоль внешних нормалей к соответствую­щим основаниям цилиндра.

Устремим в (В.20) высоту цилиндра к нулю так, чтобы основания и оставались в разных средах и в пределе совпали с элементом . Тогда, учитывая, что третье слагаемое в (В.20) стремятся к нулю (к нулю стремится площадь боковой поверхности при ограниченной подынтегральной функции), получаем следующее равенство:

, (В.21)

где и – векторы электрической индукции на элементе со стороны первой и второй среды.

Учитывая, что , и тот факт, что векторы и можно считать постоянными в пределах элемента , получаем следующее равенство:

. (В.22)

Учтем в последнем равенстве то, что , тогда

. (В.23)

Вычислим теперь правую часть соотношения (В.19) при . При этом объем цилиндра стремиться к нулю ( ). Рассмотрим случай, когда граница раздела является поверхностью идеального проводника. В этом случае на поверхности проводника распределен поверхностный заряда, т.е. .

.

Подставим последнее равенство и равенство (В.23) в соотношение (В.9), тогда получим, что

.

Сократим последнее равенство на , тогда получим следующее соотношение

. (В.24)

Соотношение (В.24) совпадает с первым соотношением в формуле (В.3).

Учитывая свойство скалярного произведения и тот факт, что , получаем следующее соотношение

. (В.25)

Последнее соотношение совпадает со вторым соотношением в формуле (В.3), т.е. определяет граничное условие в скалярной форме. Отметим, что соотношения (2.24) и (2.25) определяют граничное условие (в векторной и скалярной форме) для нормальных составляющих вектора электрической индукции в общем случае. В случае, когда граница раздела двух сред не является идеальным проводником, то в этих соотношениях надо положить .

В.4. Вывод граничных условий для нормальных составляющих векторов магнитной индукции

Рассмотрим четвертое уравнение Максвелла в интегральной форме

. (В.26)

Из сравнения уравнений (В.26) и (В.18) видно следующее. Если в уравнении (В.17) вектор поменять на вектор , а величину приравнять нулю, то оно переходит в уравнение (В.26). Отсюда следует, что вывод граничных условий для касательных составляющих векторов напряженности электрического поля (формулы (В.4)) проводится по той же методике, что и вывод, проведенный в предыдущем пункте (с учетом указанных изменений).