1.4 Построение планов ускорений

1.4.1 Высчитываем ускорение точки

1.4.2 Отложим из полюса π ускорение точки b в виде вектора

1.4.3 Масштабный коэффициент

1.4.4 По теореме о сложении ускорений для точки С составим систему уравнений:

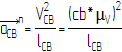
Для нулевого положения

Для десятого положения

На плане ускорений длина этого вектора

Для нулевого положения

Для десятого положения

1.4.5 Ускорение точки s₂ найдём по теореме подобия

1.4.6 Найдём ускорение шатуна

Для нулевого положения

Для десятого положения

1.4.7 По теореме о сложении ускорений для точки D составим систему уравнений:

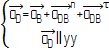
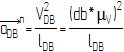
Для нулевого положения

Для десятого положения

На плане ускорений длина этого вектора

Для нулевого положения

1.4.8 Ускорение точки s₄ найдём по теореме подобия

1.4.9 Найдём ускорение шатуна

Для нулевого положения

Для десятого положения

1.4.10 Сравнительный анализ

№ положения	0	10
	658,491	221,293
	622,716	200,134
∆%	5,43	9,56

1.5 Построение кинематических диаграмм ползуна

Кинематическая диаграмма представляет собой графическое изображение изменения одного из кинематических параметров (перемещения, скорости и ускорения) точки либо звена исследуемого механизма в функции времени, угла поворота или перемещения

ведущего звена этого механизма.

1. Вычерчиваем схему механизма в масштабе µ_l в двенадцати положениях, соответствующих последовательным поворотам кривошипа AB на 30^°

2. Строим оси координат s-φ и на оси абсцисс откладываем отрезок KM=120 мм, изображающий время одного полного оборота кривошипа.

3. Отрезок l делим на 12 равных частей и в соответствующих точках 1, 2, 3… по оси координат откладываем расстояния s1, s2,…, пройденный точкой С от её верхнего положения С₀.

4. Соединяем последовательно плавной кривой полученные точки 0, 1’,2’,3’,… . Полученная

кривая будет диаграммой расстояний точки C .

Построение диаграмм скоростей и ускорений методом графического дифференцирования

Для построения диаграммы скорости поступаем так:

1. Под диаграммой (s-φ) строим оси координат 0₁V_c, 0₁φ и на продолжении оси 0₁φ влево откладываем отрезок 0₁р=Н₁ мм;

2. Из точки р проводим лучи p1; p2; p3, … параллельно хордам кривой (s_c-φ) на участках 01’;1’2; 2’3’…

Эти лучи отсекут на оси 0₁V_c отрезки 0₁1; 0₁2; 0₁3, …, пропорциональные средней скорости V_c на соответствующем участке диаграммы;

3. Отложим эти отрезки на средних ординатах соответствующих участков;

4. Соединим ряд полученных точек I;II;III, … плавной кривой; эта кривая будет диаграммой скорости (V_c-φ).

Имея диаграмму скоростей (V_c-φ), аналогично строим диаграмму тангенциальных ускорений (ω^t_c-φ).

2. Кинетостатический анализ

2.1 Определение внешних сил действующих на звенья механизма

2.1.1 Определение сил тяжести

2.1.2 Определение сил инерции

2.1.3 Определение инерционных моментов шатуна

2.2 Расчёт групп Ассура

Составим уравнение равновесия

Масштабный коэффициент

19,411 Н

2.3 Расчёт ведущего звена

2.4 Определение уравновешивающей силы с помощью рычага Жуковского

Уравновешивающий момент может быть определен при помощи теоремы Н. Е. Жуковского о «жёстком рычаге», согласно которой сумма моментов всех сил, действующих на механизм, включая силы инерции, перенесенных параллельно самим себе в одноименные точки повернутого на 90⁰ плана скоростей, относительно полюса, равна нулю.

Таким образом, план скоростей представляется как жесткий рычаг, шарнирно закрепленный в полюсе и находящийся под действием сил в равновесии.

По теореме Жуковского легко определить уравновешивающий момент.

Решение проводим в такой последовательности:

1. Строим в масштабе повернутый на 90⁰ план скоростей механизма.

2. По теореме подобия находятся на плане скоростей все точки, в которых приложены все действующие силы. Моменты сил при этом раскладываются на пары сил таким образом, что бы звено, к которому они приложены, представляло собой плечо этой пары.

Найдем уравновешивающую силу

Сравниваем значения полученные при расчете по структурным группам и при расчете по рычагу Жуковского: