3. Синтез кулачкового механизма

3.1 Построение кинематических диаграмм толкателя

Кулачковый механизм – это механизм состоящий из ведущего звена криволинейной формы (кулачка) и выходного звена (толкателя), которые образуют между собой высшую кинематическую пару.

Кинематический анализ чаще всего выполняется графическим или графоаналитическим методами.

При графическом методе сначала строится график изменения перемещения толкателя в функции фазового угла поворота кулачка, а затем методом графического дифференцирования строятся графики изменения аналогов скорости и ускорения толкателя. Этот метод позволяет выделить на графике перемещения фазовые углы, при которых толкатель поднимается, опускается или находится в состоянии покоя.

Так как сумма в 1 мм откладываем 1,5°

Масштабный коэффициент

Сравниваем угол удаления и угол возврата, для меньшего из них примем высоту графика y_в=70 мм.

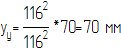
Рассчитаем полюсное расстояние

,

где h – высота толкателя;

h=45 мм

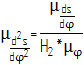
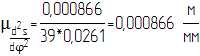
Для построения профиля кулачка достаточно иметь зависимость φ=φ(t). Площади F1 и F2, а также F2’ и F1’ должны быть равны между собой, поскольку скорость толкателя в начале и конце углов удаления и возвращения равна нулю. Проинтегрируем дважды графически заданную зависимость. Для этого:

1. построим ординаты ab, cd, …, соответствующие серединам интервалов 01, 12, …, и отложим отрезки Ob’=ab, Od’=cd на оси ординат;

2. соединим произвольно взятую точку P1 на продолжении оси Х с точками b’, d’, …;

Полученная ломаная линия (в пределе - кривая) в графической форме представляет собой

первый интеграл заданной зависимости, т.е кривую y’=y’(x), с учётом масштабов

Аналогично, интегрируя кривую y’=y’(x), получаем вторую интегральную кривую y=y(x), с учётом масштабов S=S(φ).

3.2 Определение минимального радиуса кулачковой шайбы

Точка С – центр вращения толкателя. Дуга SR радиуса l является ходом толкателя . Эта дуга размечена в соответствии с осью ординат диаграммы s - φ.

Через точки деления дуги SR из точки С проводим лучи CA₀; CA_x и т.д. На этих лучах от точкек А_i откладываем отрезки A_iL_i^’ и A_iL_i^’’, изображающие в масштабе µ_s величину , причём направление отрезков определяется поворотом вектора скорости точки А толкателя на 90^° в сторону вращения кулачка. Через концы этих отрезков проводим прямые образующие с соответствующими лучами углы γ_min. Получаем два семейства прямых: прямые первого семейства начинаются в точках L_i^’ и идут слева направо; прямые второго семейства начинаются в точках L_i^’’ и идут справа налево. Часть плоскости RDN, ограниченная пересечением двух кривых QDN и R’DT, из которых первая сгибает крайние

левые прямые первого семейства, а вторая – крайние правые прямые второго семейства, определяет геометрическое место точек, каждую из которых можно принят за центр вращения кулачка, причём при таком выборе угол передачи движения γ ни в одном положении не будет меньше γ_min.

Поместим центр вращения кулачка в точке О, находящейся внутри области RDN. Тогда отрезок 0А₀ определяет минимальный радиус r₀ кулачка, а отрезок ОС – расстояние d между центрам вращения толкателя и кулачка.

Чем дальше от точки 0 внутри области R^’DN находится центр вращения кулачка, тем лучше становятся условия работы механизма, так как углы γ увеличиваются. Однако при этом размеры механизма также увеличиваются, так как возрастает минимальный радиус r₀

кулачка и расстояние d.