Розділ 2. Рівняння вищих порядків

2.1. Теорема Коші для нормальної системи і для рівняння го порядку.

Диференціальне рівняння го порядку має вигляд

.

Якщо його можна розв’язати стосовно старшої похідної, то одержимо

. (2.1.1)

Задача Коші для рівняння (2.1.1) полягає в знаходженні розв’язку цього рівняння, який задовольняє початкові умови при

. (2.1.2)

Для доведення існування та єдиності задачі (2.1.1) – (2.1.2) замінимо рівняння (2.1.1) системою диференціальних рівнянь першого порядку з шуканими функціями. Для цього ми поряд з шуканою функцією вводимо ще допоміжних шуканих функцій , які пов’язані з та між собою співвідношеннями

. (2.1.3)

Легко побачити, що функція є похідною го порядку від функції ,

.

Тому ми маємо , і рівняння (2.1.1) запишеться у вигляді

. (2.1.4)

Рівняння (2.1.3) та (2.1.4) є системою диференціальних рівнянь першого порядку з шуканими функціями . Ліворуч у цих рівняннях стоять похідні від шуканих функцій, праві частини залежать від незалежної змінної і шуканих функцій і не залежать від похідних. Такі системи диференціальних рівнянь називають нормальними.

Система (2.1.3) – (2.1.4) має ту особливість, що тільки в останньому рівнянні права частина є функцією від змінних найбільш загального вигляду, а в рівняннях (2.1.3) праві частини мають спеціальну форму. З метою найбільшої симетрії і враховуючи, що системи диференціальних рівнянь будуть нами вивчатися пізніше, ми розглянемо нормальну систему в найбільш загальному вигляді. Для шуканих функцій ми введемо позначення . Тоді нормальна система матиме вигляд

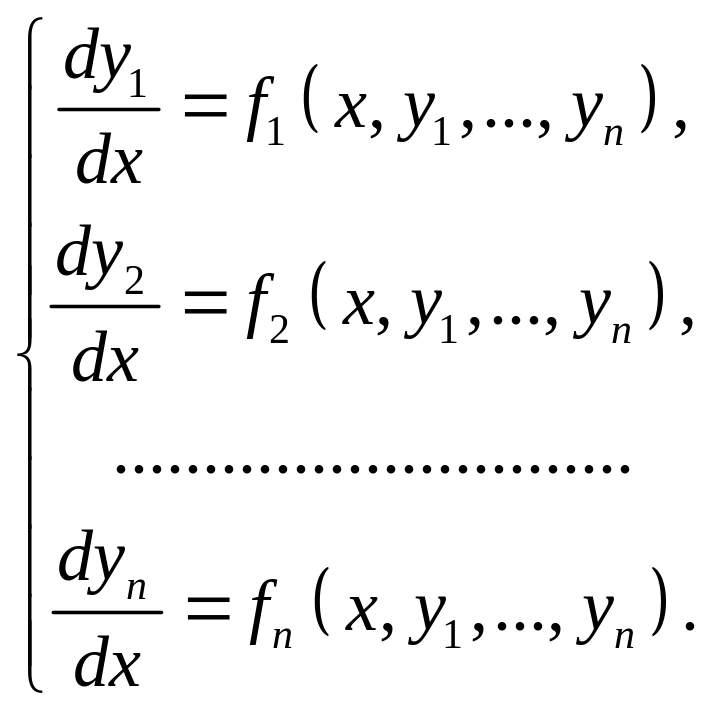(2.1.5)

Задамо початкові умови

. (2.1.6)

Теорема 2.1. (про існування та єдиність розв’язку задачі Коші для нормальної системи).

Нехай функції задовольняють такі умови:

1. Ці функції неперервні за всіма аргументами в замкненій області

.

З неперервності функцій в області випливає їх обмеженість в цій області, тобто існування такого числа , що для значень аргументів, які належать області .

2. В області ці функції задовольняють умову Ліпшиця стосовно аргументів , тобто, якщо при конкретному значенні для довільних точок і виконуються нерівності

,

де є деяке додатне число.

Тоді задача Коші (2.1.5) – (2.1.6) має єдиний розв’язок, визначений на відрізку , де .

Варто зауважити, що згідно з теоремою Лагранжа умова Ліпшиця виконується при існуванні і неперервності в області частинних похідних .

Теорема 2.1 є узагальненням теореми Коші для рівняння , тому займатися детальним доведенням цієї теореми немає потреби.

Згадаємо тепер, що рівняння (2.1.1) зводилося до нормальної системи спеціального виду. Застосовуючи теорему 2.1 до цієї системи, можемо сформулювати теорему існування та єдиності розв’язку задачі Коші для рівняння (8.1).

Теорема 2.2. Задача Коші (2.1.1) – (2.2.2) має єдиний розв’язок, якщо права частина рівняння (8.1) неперервна за всіма аргументами і задовольняє умову Ліпшиця по аргументам .

Як наслідок з цієї теореми ми можемо одержати таке твердження: загальний розв’язок рівняння го порядку залежить від довільних сталих і має вигляд

.

Якщо співвідношення між і довільними сталими одержано в неявному вигляді

,

то ми називатимемо таке співвідношення загальним інтегралом рівняння.