8.6.2. Оценка вероятностей правил подстановки с помощью процедур обучения

Переход от детерминированной к стохастической грамма­тике осуществляется относительно просто. Единственное разли­чие между этими двумя типами грамматик заключается в на­личии или отсутствии множества вероятностных мер для правил подстановки Q. Естественно, если мы хотим использовать сто­хастические грамматики, необходимо обладать механизмом оценки этих вероятностей.

Рассмотрим задачу разделения М. классов, характеризую­щуюся стохастическими грамматиками

Предполагается, что V _Nq , V _Tq, Р_q и S, известны и грамматики однозначны. Так как все еще существует множество нерешен­ных задач, связанных с оценкой вероятностей правил подста­новки, мы сосредоточим наше внимание только на бесконтекст­ных и регулярных грамматиках. Учитывая это ограничение, тре­буется оценить вероятности правил подстановки Q_q , q = 1, 2. ..., M, при помощи множества выборочных терминальных цепочек

Т={х_1, х₂..., х_m}, (8.6.8)

где каждая цепочка принадлежит языку, порожденному одной из стохастических грамматик вида (8.6.7).

Собрав все цепочки, перенумеруем их и обозначим через n(x_n) количество появлений цепочки Хn. Каждая цепочка под­вергается также разбору с помощью каждой грамматики, и число N_q^ij(Хn } обозначает, сколько раз при грамматическом разборе цепочки Хn применялось правило подстановки A_i—>β_j грамматики G_q. Хотя вероятности правил подстановки грамма­тик (8.6,7) нам не известны, предполагается, что сами правила подстановки мы знаем, поэтому грамматический разбор воз­можен.

Математическое ожидание n_q^ij числа вхождений правила подстановки A_i—>β_j; грамматики G_q в грамматический разбор данной цепочки можно аппроксимировать следующим выра­жением:

где p(G_qlx_n)—вероятность порождения данной цепочки х_n грамматикой G_q. В процессе обучения эта вероятность должна быть определена для каждой цепочки.

Всроятность р_qij применения правила подстановки A_i—>β_j в грамматике G_q может теперь быть аппроксимирована соот­ношением

где р^{^}_qij—оценка вероятности р_qij. а суммирование в знамена­теле (8,6.10) выполняется по всем правилам подстановки грам­матики G_q имеющим вид A_i—>β_k т. е. для всех правил под­становки грамматики Gq с одинаковой нетерминальной левой частью Ai.

Как было показано Ли и фу [1972], но мере приближения числа цепочек в T к бесконечности оценка вероятности р^{^}_qij; при­ближается к истинной вероятности правила подстановки р_qij при выполнении следующих условий:

1. 

   Множество Т— репрезентативное подмножество языков L{Gq}, q=1, 2, .,., М, в том смысле, что Т->L. где L—объ­единение языков, т. е.

2. Оценка вероятности появления цепочки х_n, в множестве T, определяемая соотношением

приближается к истинной вероятности р(х_л).

3. В процессе обучения для каждой цепочки Xn, может быть определена вероятность р(Gq|x_n).

Вероятность р(Gq|x_n) того. что данная цепочка x_n принад­лежит классу w_q, обычно без труда может быть установлена в обучающей фазе. Если определенно известно, что данная це­почка принадлежит исключительно классу w_q, то р(Gq|x_n) = 1. Аналогично, если известно, что Х_n не может принадлежать w_q, то р(Gq|x_n) = 0. Часто, однако, вследствие обсужденных в на­чале этого раздела причин некоторые цепочки могут принад­лежать более чем одному классу. В этом случае можно полу­чить простую оценку вероятности р(Gq|x_n), q= 1, 2, .... М, для этих цепочек, фиксируя относительную частоту, с которой они встречаются в каждом классе. При этом, конечно, необхо­димо, чтобы.

(8.6.12)

Когда невозможно определить относительную встречаемость «неоднозначных» цепочек в каком-либо определенном классе, наиболее оправданным для этих цепочек считается обычно до­пущение р(Gq|x_n) == 1/М.

Пример. Проиллюстрируем представленные в этом пара­графе понятия простым числовым примером. Рассмотрим сто­хастические грамматики

где для обеих грамматик

Правила подстановки и соответствующие им вероятности за­даны следующим образом:

Требуется определить с помощью обучающей процедуры ве­роятности, входящие в q₁ и Q₂.

Для того чтобы не отклоняться от принятой ранее системы обозначений, можно изменить приведенные выше обозначения следующим образом:

где мы задаем S = А₁, β₁= aS, β₂ = а, β₃ = bS, β₄ = Ь. Ин­дексы вероятностей интерпретируются так же, как и раньше, т. е, первый индекс представляет класс, второй означает индекс левой части правила подстановки, третий—индекс правой ча­сти правила подстановки. В данном случае все левые части идентичны.

Для наглядности предположим, что класс w₁ включает в себя только цепочки, составленные из символов a, а класс w₂—только цепочки из символов Ь. Однако вследствие вмеша­тельства шума иногда могут встречаться и смешанные цепочки. Отметим, что, хотя обе грамматики G₁и G₂могут порождать смешанные цепочки, в этом примере мы будем считать, что G₁ используется только для порождения цепочек, состоящих из а, и G₂ используется только для порождения цепочек, состоящих из Ь. Предположим далее, что обучающая выборка состоит из 100 образов-цепочек со следующими характеристиками:

цепочка	Число появлений цепочки
а	30
аа	20
ааЬЬЬ	5
ЬЬ	25
Ь	20

Обозначив первый тип цепочки х₁, второй— х₂ и т. д., получаем

Для оценки вероятностей р_qij по формуле (8-6.10) необходимо сначала вычислить значения n_qij. Согласно (8.6.9),

где Т состоит из 30 цепочек x₁, 20 цепочек х₂ и т, д. Используя это соотношение, мы получаем для дласса w₁

Проанализируем это выражение более подробно. Величина n{x₁) известна, a p(G₁|x₁) есть вероятность того, что цепочка х₁ принадлежит к классу w₁. Можно предположить, что эта ве­роятность равна 1, поскольку х₁ состоит только из элементов а. Коэффициент N₁₁₁(x₁)—число использовании в грамматическом разборе цепочки X₁ правила A₁->β₁. Так как видно, что это правило подстановки не участвует в разборе x₁, то N₁₁₁(x₁)=0. Аналогичным образом вычисляется второе слагаемое. Третья цепочка содержит как символы а, так и b и поэтому может принадлежать любому из двух классов. Допуская, что вероят­ности ее принадлежности классу w₁ и классу w₂ равны, считаем p(G₁| x₃) == 0.5. В общем случае, как упоминалось ранее, знание конкретной информации о задаче помогает определять эти ве­роятности более осмысленно. Цепочки х₄ и х₅ в четвертом и пя­том слагаемых относим к w₂, поскольку они состоят исключи­тельно из символов Ь. Отметим также, что N₁₁₁(x₄)= N₁₁₁(x₅)=0, поскольку правило A₁->β₁не участвует в грам­матическом разборе этих цепочек. Учитывая все эти соображе­ния, получаем

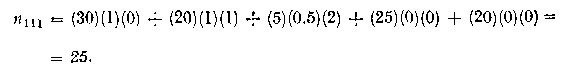
x1	о	1	о	о
x2	1	1	о	о
x3	2	о	2	1
x4	0	о	1	1
x5	о	о	о	1

Подставляя эти значения, вычисляем остальные n_qij, что при­водит к

n₁₁₂ = (30)(1)(1) +(20)(1)(1)+ + (25)(0)(0) + (20)(0)(0) = 50

n₁₁₃ = (30)(1)(0) + (20)(1)(0) + (5)(0.5)(2) + (25)(0)(1) + (20)(0)(0) = 5

n₁₁₄= (30)(1)(0) + (20)(1)(0) + (5)(0.5)(1) + (25)(0)(1) + (20)(0)(1) = 2,5.

Теперь можно подсчитать все вероятности для класса w₁ по формуле

где суммирование производится по всем правилам подстановки грамматики g₁ с одинаковой нетерминальной левой частью A_i.

В нашем примере все левые части правил подстановки иден­тичны. Следовательно,

Как и ожидалось, правила подстановки класса w₁, связанные с порождением цепочек из элементов а, обладают большей ве­роятностью.

Вычисление вероятностей правил подстановки для класса w₂ аналогично только что проделанной процедуре. Из того, что правила подстановки этих двух грамматик идентичны, вытекает N_2ij{x_h) = N1ij(x_n). Использование для этих величин значений, приведенных ранее в таблице, приводит к следующим п_2ij:

В данном случае х₁ и х₂ несомненно принадлежат классу w₁, поэтому можно предположить, что p(G₂,\x₁) == p(G₂,\x₂) = 0. Аналогичным образом p(G₂,\x₄) == p(G₂,\x₅)=1 Кроме того, из нашего допущения о разбиении точно на два класса вытекает, что p(G₂,\x₃)=1-p(G₁,\x₃)=0.5.. Используя эти вероятности, а также табличные значения, получаем

Вероятности правил подстановки могут теперь быть вычислены при помощи соотношения

где, как и ранее, суммирование происходит по всем правилам подстановки грамматики G₂, имеющим одинаковую нетерми­нальную левую часть А_i в данном случае это верно для всех правил подстановки. Использование приведенного соотношения дает следующий результат:

Вычислив по выборочным цепочкам вероятность всех пра­вил подстановки, теперь можно полностью определить стохасти­ческую грамматику для данного примера:

8.7. ОБУЧЕНИЕ И ГРАММАТИЧЕСКИЙ ВЫВОД

Главы 3—6 были посвящены в основном проблеме построе­ния решающих функций с помощью обучающих выборок. В этой главе эта задача до сих пор умышленно не упомина­лась. Используя лингвистическую терминологию, процедуру получения решений с помощью обучающей выборки легко ин­терпретировать как задачу получения грамматики из множе­ства выборочных предложений. Эта процедура, обычно назы­ваемая грамматическим выводом'), играет важную роль в изу­чении синтаксического распознавания образов в связи с ее значением для реализации автоматического обучения. Тем не менее, как это станет ясно из последующего обсуждения, об­ласть грамматического вывода находится еще в начальной ста­дии развития. Мы имеем в виду возможности обучения, которые можно было бы считать приемлемыми для синтеза универсаль­ных методов построения систем синтаксического распознавания образов. Этот параграф посвящен в основном введению понятий грамматического вывода, рассматриваемых с двух точек зре­ния. В п. 8.7,1 строится алгоритм для вывода некоторых клас­сов цепочечной грамматики. Затем в п. 8.7.2 достаточно по­дробно разбирается задача вывода двумерных грамматик. Хотя грамматики деревьев быстро становятся важной темой иссле­дований в синтаксическом распознавании образов, алгоритмы вывода подобных грамматик, на наш взгляд, еще не достигли уровня, позволяющего включать их в учебник. В качестве вве­дения в эту область можно рекомендовать читателям работу Гопсалеса и Томасона |1974б].

---------------------------------------------

') В литературе можно встретить также термин «восстановление грамма­тики». — Прим. перце.

---------------------------------------------