4. Дискретные экспоненциальные функции

В дискретном преобразовании Фурье используется система дискретных экс­поненциальных функций (ДЭФ), которая определяется следующим выражением:

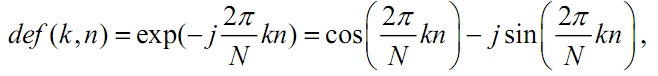
где ; k и n принимают целочисленные значения (0,1,2,...,N - I). Пере­менную k отождествляют с номером функции, а переменную n — с номером от­счета.

Введем обозначение .

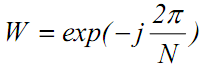Т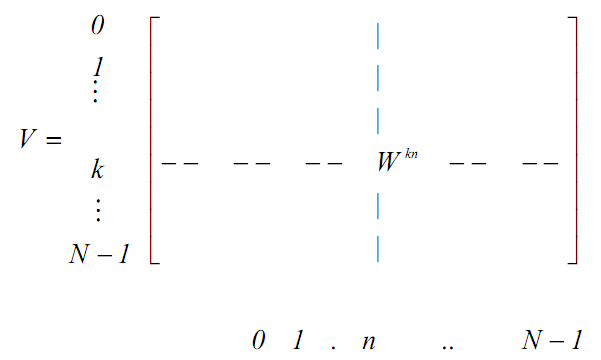 огда

Всю систему ДЭФ можно записать в виде матрицы V, строки которой нумеруются переменной k, столбцы переменной n, а в пересечении k-й строки и п-го столбца записана величина W ^nk. Такое представление называется матричным представлением ДЭФ.

Основные свойства дэф

1. Ортогональность:

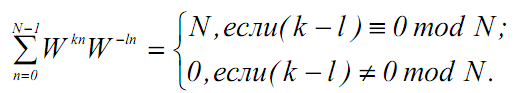
Показывает, что скалярное произведение любых двух строк матрицы V, одна из которых взята с комплексно сопряженными эле­ментами, равно нулю, если строки различны, и равно N, если они совпадают. Мат­ричная запись этого свойства имеет следующий вид:

где знак * означает взятие комплексного сопряжения для всех элементов матрицы (I - единичная матрица).

^{2. Периодичность.}

^{Если ,} что позволяет за­писать элементы матрицы V с минимальными степенями (фазами).

^{3. Симметричность:}

Позволяет легко найти обратную матрицу для матрицы V. Матричное выражение для ортогональности запишется:

^{4. Мультипликативность:}

по номеру функции:

по номеру отсчета:

Означает, что при умножении любых двух строк (столбцов) матри­цы V получается соответственно строка (столбец) той же матрицы номер строки (столбца) равен сумме номеров сомножителей.

ДЭФ можно изобразить на плоскости в виде вращающегося вектора единичной длины, проек­ции которого на оси абсцисс и ординат дают действительную и мнимую части функции. Разница будет заключаться в том, что если у обычных функций этот вектор вращается непрерывно, то в случае ДЭФ он вращается скачкообразно. Такому представлению соответствует запись систе­мы ДЭФ в виде матрицы с полными фазами, а матрица с минимальными фазами не дает представления об истинной скорости вращения вектора. Поэтому величину W^kn называют поворачивающим множителем.

По формуле Эйлера можно выразить значения вещественной и мнимой час­тей поворачивающих множителей через косинус и синус угла поворота соответ­ственно:

.

5. Дискретное преобразование Фурье и его свойства

Пара дискретного преобразования Фурье последовательности {s(n)} = {s(0),s(1),...,s(N – 1)} определяется следующими равенствами:

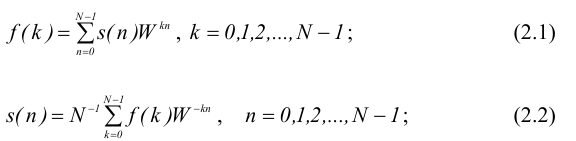
где {f(к)}- дискретный спектр.

Выражение (2.1) называется прямым преобразованием, а выражение (2.2) -обратным.

В матричной форме ДПФ имеет вид:

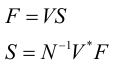
Основные области применения ДПФ:

• цифровой спектральный анализ

• быстрое преобразование Фурье (БПФ)

Свойства дпф[8]:

1. Периодичность, В силу периодичности ДЭФ функции f(к) и s(n) также периодичны, т. е.:

2. Связь с коэффициентами ряда Фурье.

При дискретизации периодической аналоговой функций s(t) ДПФ позволяет по выборкам s(п) найти спектр f(к), который на интервале 0 < к <N-1 равен спектру исходной функции s(t).

3. Линейность. Пусть даны последовательности х(п) и у(п), для которых ДПФ равны соответственно f_x(k) и f_y(k). Рассмотрим взвешенную сумму этих последовательностей z(n) = ах(п) + bу(п). Спектр последовательности z(n) равен аналогичной взвешенной сумме спектров последовательностей х(п) и у(п),т. е.:

4. Инвариантность относительно сдвига но времени и частоте.

При сдвиге по времени амплитудный спектр не меняется. Изменениям подвергаются только фазы гармонических составляющих.

5. Теорема о свертке.

Теорема о свертке утверждает, что спектр свертки равен произведе­нию спектров сворачиваемых последовательностей:

Матричное представление свертки имеет вид:

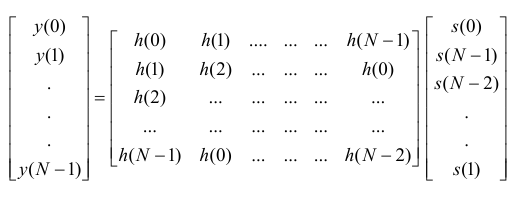
6. Теорема о корреляции.

Спектр корреляционной функции последовательностей {s(n)} и {h(n)}равен произведению их спектров, причем один из спектров берётся в комплексном со­пряжении, т. е.:

Матричное представление корреляции:

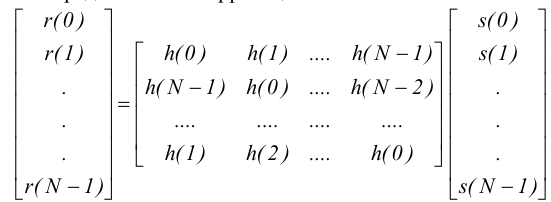
7. Д 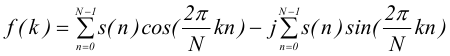ПФ вещественных последовательностей.

Отсюда особенности:

а) спектральные коэффициенты комплексно сопряжены относительно счета 2/N

б) если последовательность {s(n)} четная, то её ДПФ вещественная последовательность. Аналогично, если {s(n)} - нечетная, то ее ДПФ чисто мнимая последовательность.

8. Равенство Парсеваля:

Э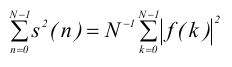 нергия сигнала равна суммарной энер­гии спектральных компонент, т.е. энергия сигнала больше никуда не расходуется.