24. Обработка бинарных изображений на основе математической морфологии
Математическая морфология - относительно новый подход в обработке изображений, суть которого заключается в том, что исходное изображение рассматривается как множество, и к нему применяются теоретико-множественные операции.
Пусть X ⊆E есть множественное представление двоичного входного изображения, и пусть B ⊆E есть компактное множество малого размера и простой формы. Множество В называется структурирующим элементом.
Фундаментальными морфологическими операторами для множеств являются наращение ⊕ и эрозия –:
Расширение:
Эрозия:
Операции расширения и эрозии обладают свойствами:
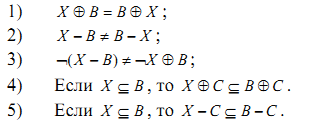
В результате выполнения эрозии исчезнут объекты, чей диаметр меньше структурирующего элемента. В результате же выполнения расширения могут закраситься впадины в объектах и пустоты в изображениях, чей диаметр меньше структурирующего элемента.
В результате выполнения морфологических операций в изображении остаются лишь те симметрии, которые присутствуют в структурирующем элементе. Поэтому, для того чтобы в результате обработки изображения не внести в него новых искажений, структурирующий элемент должен быть близок к кругу.
Отмыканием множества А множеством В (А°В) называется последовательное применение операций эрозии и расширений.
Замыканием множества А множеством В (А•В) называется последовательное применение операций расширения и эрозии
На практике операция закрывания применяется для смыкания дыр в объектах, но только таких дыр, диаметры которых не превышают диаметра структурирующего элемента. Операция открывания может быть использована для разделения объектов на бинарном изображении. Здесь сложность состоит в правильном выборе размеров структурирующего элемента.
27. Обработка полутоновых изображений на основе математической морфологии
Математическая морфология - относительно новый подход в обработке изображений, суть которого заключается в том, что исходное изображение рассматривается как множество, и к нему применяются теоретико-множественные операции.
Здесь применяются операции расширение, эрозия, открывание и закрывание.
Для простоты считается, что коэффициенты в структурирующем элементе B равны нулю.
Тогда расширение для полутоновых изображений запишется в следующем виде:
Также определим операцию эрозия:
В результате выполнения эрозии исчезнут объекты, чей диаметр меньше структурирующего элемента. В результате же выполнения расширения могут закраситься впадины в объектах и пустоты в изображениях, чей диаметр меньше структурирующего элемента.
Открывание есть последовательное применение операций эрозии и расширения, а закрывание – последовательное
применение операций расширения и эрозии.
Открывание:
Закрывание:
С помощью математической морфологии можно проводить сглаживание изображения. Определяя математически, эта операция есть последовательное применение открывания и закрывания к исходному изображению:
Следующей очень важной операцией является нахождение морфологического градиента, который может быть использован для выделения контуров на изображении и определяется следующим образом:
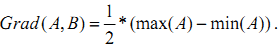
Изолирование (выделение) полутоновых объектов может быть выполнено при помощи преобразования, предложенного Мейером:
Размеры структурирующего элемента должны быть выбраны большими, чем размеры объектов на изображении.