4.3.3 Принцип максимума
Метод принципа максимума разработан
Л.С. Понтрягиным и является расширением
классического вариационного исчисления
на случай, когда управляющие воздействия
ограничены и описываются кусочно-непрерывными
функциями. Задачей оптимизации тогда
является определение оптимальных
управлений
и траекторий
из условия нахождения экстремума
функционала
(4.5)
для заданных уравнений объекта управления
(4.6)
при начальных и конечных значениях
и
,
а также заданном интервале времени
с учетом ограничений
<
и
.
В общем случае ММ объекта оптимизации имеет вид Коши
или
(4.7)
При оптимизации объекта требуется
определить вектор управляющего
воздействия
с учетом ограничений из условия минимума
функционала
. (4.8)
В рассмотрение вводят вектор вариации траектории
.
Закон изменения вариации, являющейся бесконечно малой величиной, выводят из уравнения в вариациях
.
(4.9)
С помощью функции Гамильтона для неклассических вариационных задач
,
(4.10)
где
, системы (4.7) и (4.9) записывают в виде
системы канонических уравнений Гамильтона
для неклассических вариационных задач,
которые справедливы и для классических
, (4.11)
где
.
Необходимые условия оптимальности
управления формулируют следующим
образом: чтобы управление
и соответствующая ему траектория
были оптимальны, необходимо существование
ненулевой векторной функции
,
составляющие которой
…
удовлетворяли бы системе уравнений
(4.11), чтобы при
функция Гамильтона Н* достигла
максимума при
т.е.
,
а в конечный момент t=T выполнялись бы также соотношения
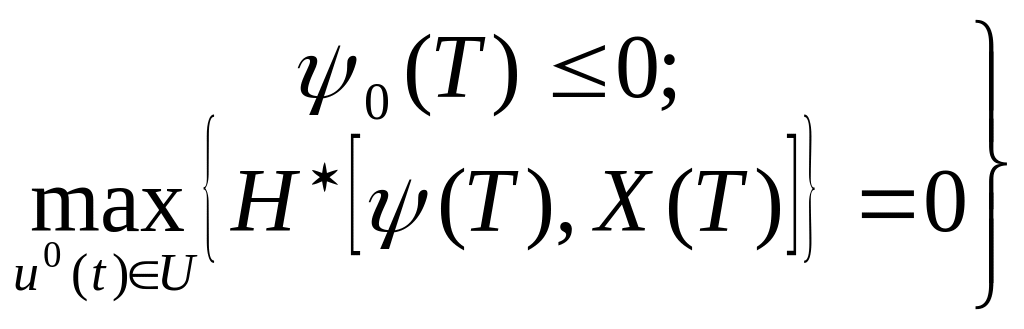(4.12)
(при этом принимают
).
Следовательно, при оптимизации САУ
с использованием принципа максимума
составляют функцию Гамильтона (4.10)
записывают уравнения (4.11), из которых
находят оптимальные управления
и
.
При этом решение задач оптимизации
сводится к решению дифференциальных
уравнений в многомерном пространстве.
Расчет максимальной функции Гамильтона
Н
(u)
определяет название метода. Этот метод
применяют при синтезе максимально
быстродействующих САУ.
4.3.4 Метод динамического программирования.
В основу этого метода, разработанного
Беллманом Р., положен принцип
оптимальности, согласно которому
оптимальное управление САУ не зависит
от предыстории самой системы. Метод
динамического программирования дает
возможность найти оптимальные управления
и траектории
из условия минимума функционала (4.5) для
заданных уравнений объекта управления
(4.6), начальных и конечных значений
и
и интервала времени
при наличии ограничений
и
.
Если необходимо обеспечить максимум
функционала (4.5), следует принять знак
минус перед интегралом.
Для решения поставленной задачи оптимизации используют вспомогательную функцию Беллмана
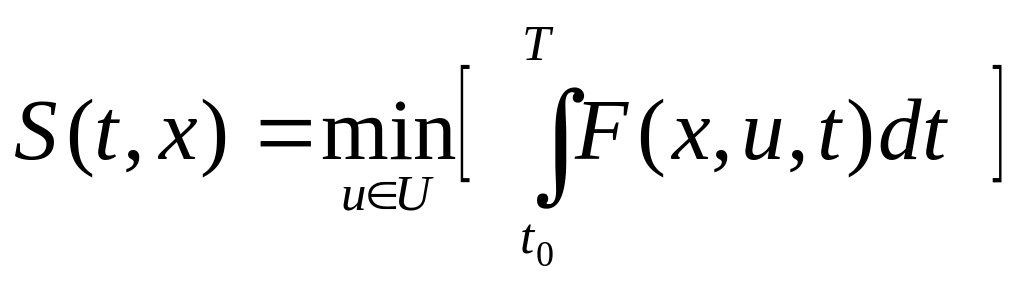(4.13)
и нелинейное дифференциальное уравнение
Беллмана в частных производных
относительно функции
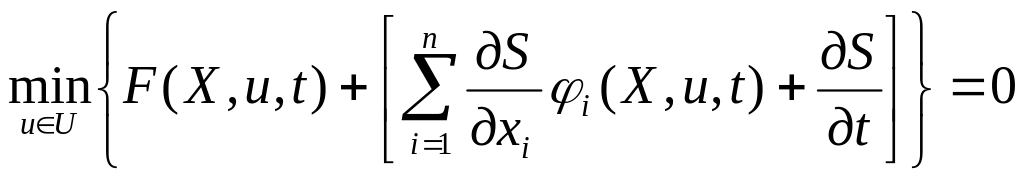(4.14)
при следующих условиях:
;
u(t)
;
.
Решением этого уравнения находят
оптимальное управление
.
Соответственно полученной функции
по уравнению (4.6) определяют оптимальную
траекторию вектора
.
Если уравнение Беллмана невозможно
решить аналитически, то применяют
численные методы.